Logistic Growth
TLDRIn this video, Mr. Andersen explains the concept of logistic growth, which occurs after a population reaches a carrying capacity or limit. He begins with an example of rabbit population growth, illustrating how the growth rate (r) is influenced by births and deaths. Initially, the population exhibits exponential growth, but eventually, it levels off as it approaches the carrying capacity (K), which is the maximum population size an ecosystem can support. The video uses the NetLogo model 'Rabbits, Grass and Weeds' to demonstrate how the rabbit population fluctuates with the availability of grass. The logistic growth equation is introduced, showing how it accounts for the carrying capacity. The video also discusses r-selected and K-selected species, with r-selected species having rapid growth and K-selected species investing more in fewer offspring for survival. The summary concludes by noting that logistic growth is characterized by quick growth that eventually reaches an environmental limit.
Takeaways
- 📈 **Exponential vs. Logistic Growth**: Exponential growth occurs when the growth rate (r) is greater than zero, leading to a 'J' shaped curve, whereas logistic growth eventually levels off as it approaches a carrying capacity (K).
- 🐰 **Population Dynamics**: The initial example uses rabbits to illustrate how population growth can change over time, influenced by birth and death rates.
- 🌱 **Limiting Factors**: Environmental factors such as available resources (like grass for rabbits) act as limiting factors that constrain population growth, leading to logistic growth patterns.
- 🌿 **Carrying Capacity (K)**: Defined as the maximum population size that an ecosystem can support, it is a critical concept in logistic growth models.
- 🐘 **Darwin's Observations**: Charles Darwin noted that even with a high reproductive rate, species like elephants would eventually hit a population limit due to the time it takes to reach reproductive age.
- 🚫 **Non-Sustainability of Exponential Growth**: Exponential growth is unsustainable in the long term as it will eventually outstrip the available resources.
- 🧵 **Modeling Logistic Growth**: Students used creative methods like Minecraft to model logistic growth, demonstrating how population growth slows as it approaches carrying capacity.
- 🔢 **NetLogo Simulation**: The Rabbits, Grass, and Weeds model in NetLogo shows how rabbit populations and grass resources fluctuate, eventually stabilizing at a carrying capacity.
- 📉 **Resource Depletion and Population Crash**: When resources are depleted faster than they can regenerate, the population of consumers (like rabbits) will crash.
- 🔁 **Cycles of Growth and Decline**: The script illustrates how populations and resources can fluctuate in a cycle, with the population eventually stabilizing at a certain level.
- ➡️ **Mathematical Representation**: The logistic growth equation is derived from the exponential growth equation by incorporating a factor that slows growth as the population approaches carrying capacity.
- 🌳 **r-selected and K-selected Species**: r-selected species (like the frog) have rapid growth and produce many offspring, while K-selected species (like the chameleon) have slower growth and invest more in fewer offspring, leading to different population dynamics.
Q & A
What is logistic growth?
-Logistic growth is a model of population growth that includes carrying capacity, which is the maximum population size that an environment can sustain indefinitely. It occurs after exponential growth, when a population reaches a limit due to environmental constraints.
What is the difference between exponential growth and logistic growth?
-Exponential growth occurs when a population size increases at a rate proportional to its current size, leading to a rapid and continuous increase. Logistic growth, on the other hand, initially increases rapidly like exponential growth but then slows down as it approaches the carrying capacity of the environment.
What does the 'r' in logistic growth represent?
-In logistic growth, 'r' represents the growth rate of the population. It is determined by the difference between the birth rate and the death rate, which can vary based on factors like resource availability.
What is the 'carrying capacity' (K) in logistic growth?
-The carrying capacity (K) is the maximum population size that an environment can sustain indefinitely. It is the limit that the population growth reaches due to environmental constraints such as food availability, space, and other resources.
How does the availability of resources affect logistic growth?
-The availability of resources directly affects logistic growth by influencing the carrying capacity. If resources are abundant, the carrying capacity may be higher. Conversely, if resources are scarce, the carrying capacity will be lower, leading to slower population growth and potentially a population decline.
What is the 'J' shaped curve in population growth?
-The 'J' shaped curve is characteristic of exponential growth, where the population size increases rapidly over time without any constraints. It is called 'J' shaped because when graphed, the curve resembles the letter 'J'.
What is the role of the birth and death rates in determining the growth rate 'r'?
-The growth rate 'r' is calculated as the net difference between the birth rate and the death rate, divided by the original population size (N). A positive 'r' indicates growth, while a negative 'r' indicates a declining population.
How do r-selected and K-selected species differ in their growth strategies?
-r-selected species are adapted for rapid growth in unstable environments, producing many offspring with minimal parental care, expecting high mortality among the offspring. K-selected species, on the other hand, invest heavily in fewer offspring, providing more parental care to ensure their survival, and are adapted to stable environments with limited resources.
What is the significance of the logistic growth model in understanding real-world population dynamics?
-The logistic growth model is significant because it provides a more realistic representation of how populations grow under environmental constraints. It helps predict how populations may change over time in response to factors such as resource availability, predation, and competition.
How does the logistic growth model account for environmental limitations?
-The logistic growth model accounts for environmental limitations by incorporating a carrying capacity (K). As the population size (N) approaches K, the growth rate slows down, preventing the population from exceeding the environment's capacity to support it.
What are some real-world examples of logistic growth?
-Real-world examples of logistic growth can be seen in the population dynamics of species such as rabbits in a limited grassland area, or bacteria in a confined environment with limited nutrients. These populations initially grow exponentially but eventually stabilize as they approach the carrying capacity of their environment.
How does the logistic growth model apply to human population growth?
-The logistic growth model can apply to human population growth by considering factors like resource availability, technological advancements, and social structures that influence birth and death rates. It suggests that human populations may initially grow exponentially but will eventually stabilize as they approach the carrying capacity of the Earth's resources.
Outlines
🐰 Introduction to Logistic Growth
Mr. Andersen introduces the concept of logistic growth, which is a model for population growth that takes into account the carrying capacity of the environment. He explains that logistic growth occurs after exponential growth, when a population reaches a limit or 'carrying capacity'. The video begins with a hypothetical scenario involving two rabbits, highlighting the role of birth and death rates in population change. The growth rate (r) is calculated by the number of births minus deaths, divided by the original population size (N). The video emphasizes that exponential growth, where r > 0, leads to rapid population increase, which is unsustainable in nature due to limited resources.
🌿 Carrying Capacity and Limiting Factors
The video discusses the concept of carrying capacity (K), which is the maximum population size that an ecosystem can support. It illustrates how resources like grass, which rabbits consume, limit population growth. As the rabbit population increases, they deplete the grass, leading to a decline in the rabbit population until it stabilizes at the carrying capacity. Mr. Andersen also mentions Charles Darwin's observations on the unsustainable nature of exponential growth, even in long-lived species like elephants. The video presents two models to demonstrate logistic growth: a Minecraft simulation and a NetLogo model called 'Rabbits, Grass, and Weeds,' which show how population dynamics fluctuate around the carrying capacity.
📈 Logistic Growth Equation and Species Selection
The video transitions into the mathematical representation of logistic growth, contrasting it with exponential growth. The logistic growth equation is presented, incorporating the carrying capacity (K) into the growth rate formula. The video demonstrates how the growth rate slows as the population size (N) approaches the carrying capacity (K), leading to a stabilization in population growth. It also introduces the concepts of r-selected and K-selected species, which refer to species adapted to rapid growth and those adapted to stable environments, respectively. The video concludes with a discussion on human population growth, which invests heavily in offspring survival, leading to a gradual approach to carrying capacity without drastic boom and bust cycles.
Mindmap
Keywords
💡Logistic Growth
💡Exponential Growth
💡Carrying Capacity (K)
💡Growth Rate (r)
💡Population Size (N)
💡Limiting Factors
💡r-Selected Species
💡K-Selected Species
💡Resource Availability
💡Environmental Constraints
💡Modeling
Highlights
Logistic growth occurs after a population finds a carrying capacity or crashes.
The growth rate (r) is determined by the number of births and deaths.
An example of exponential growth is given with a growth rate of 1, leading to a rapid increase in population size.
Darwin's observation on elephant reproduction and the impossibility of sustained exponential growth is discussed.
The concept of carrying capacity (K) as the maximum population size an ecosystem can support is introduced.
A Minecraft model of logistic growth is described, where chickens represent the population growth within a confined space.
The NetLogo model 'Rabbits, Grass and Weeds' is used to demonstrate how population dynamics work with limited resources.
The logistic growth equation is derived from the exponential growth equation by incorporating a carrying capacity factor.
As population size increases, limiting factors slow growth, leading to a leveling off at the carrying capacity.
The difference between r-selected and K-selected species in terms of growth rate and resource utilization is explained.
Human population growth is characterized by a gradual increase towards a carrying capacity, reflecting our K-selected strategy.
Trees are discussed as an example of species that may fall between r-selected and K-selected categories due to their slow growth and numerous offspring.
Logistic growth is defined as rapid growth that eventually reaches a limit based on environmental constraints.
The video emphasizes the importance of understanding population dynamics and the role of carrying capacity in ecological systems.
The mathematical representation of logistic growth is shown to illustrate how population growth slows as it approaches the carrying capacity.
The video concludes by reinforcing the concept of logistic growth and its relevance to real-world ecological scenarios.
Transcripts
Browse More Related Video

Logistic growth versus exponential growth | Ecology | AP Biology | Khan Academy
Logistic Growth (Separable Differential Equations)

Exponential and logistic growth in populations | High school biology | Khan Academy

Logistic Differential Equation
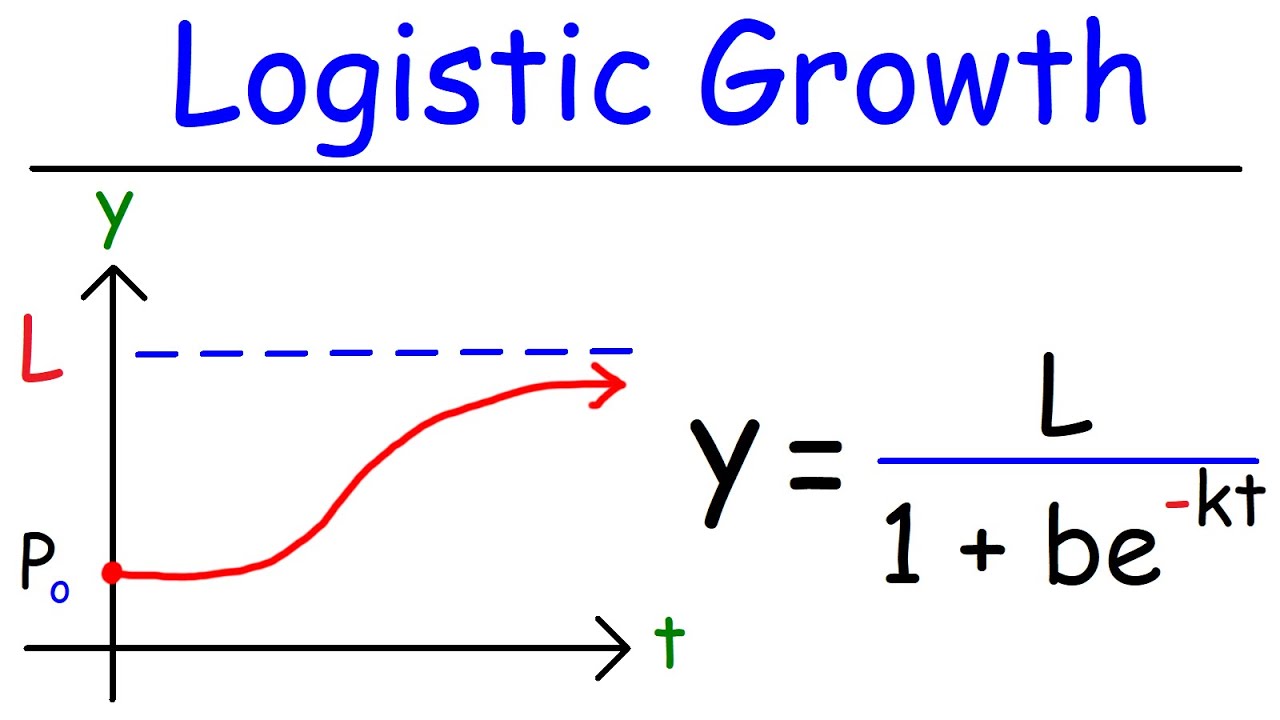
Logistic Growth Function and Differential Equations

AP Calculus BC Lesson 7.9
5.0 / 5 (0 votes)
Thanks for rating: