Logistic growth versus exponential growth | Ecology | AP Biology | Khan Academy
TLDRThe video script discusses the concept of population growth, introducing the per capita growth rate denoted by 'r'. It explains that a per capita growth rate of 0.2 implies an average increase of 20% per individual in a year. The script explores the idea of maximum per capita growth rate, which assumes no limitations on resources. An exponential growth equation is derived from this concept, where the rate of population change is the product of the maximum per capita growth rate and the population size. The video then contrasts exponential growth with logistic growth, which incorporates a carrying capacity (K) to model how population growth slows as it approaches the environment's limit. The logistic growth model is represented mathematically and demonstrated through examples at different population sizes. The script concludes by illustrating the difference between the two growth models graphically, emphasizing the unrealistic nature of unlimited exponential growth versus the more realistic logistic growth that levels off at the carrying capacity.
Takeaways
- 📈 The per capita growth rate (r) represents the average increase in population size per individual per year. For example, a rate of 0.2 means a 20% increase per individual.
- 🌱 In sexually reproducing populations, you need at least a male and a female, but some organisms can reproduce asexually through budding or division, especially unicellular ones.
- ✖️ The maximum per capita growth rate assumes no limitations such as resource scarcity, which is an ideal but unrealistic scenario.
- 📚 The exponential growth equation is dN/dt = r * N, where dN/dt is the rate of population change over time, r is the per capita growth rate, and N is the population size.
- 🔢 For a population of 100, the growth rate is 20 individuals per year. For 500, it's 100 individuals, and for 900, it's 180 individuals, all calculated using the exponential growth formula.
- 🌿 The concept of carrying capacity (K) introduces a limit to population growth based on environmental limitations such as food, water, and space.
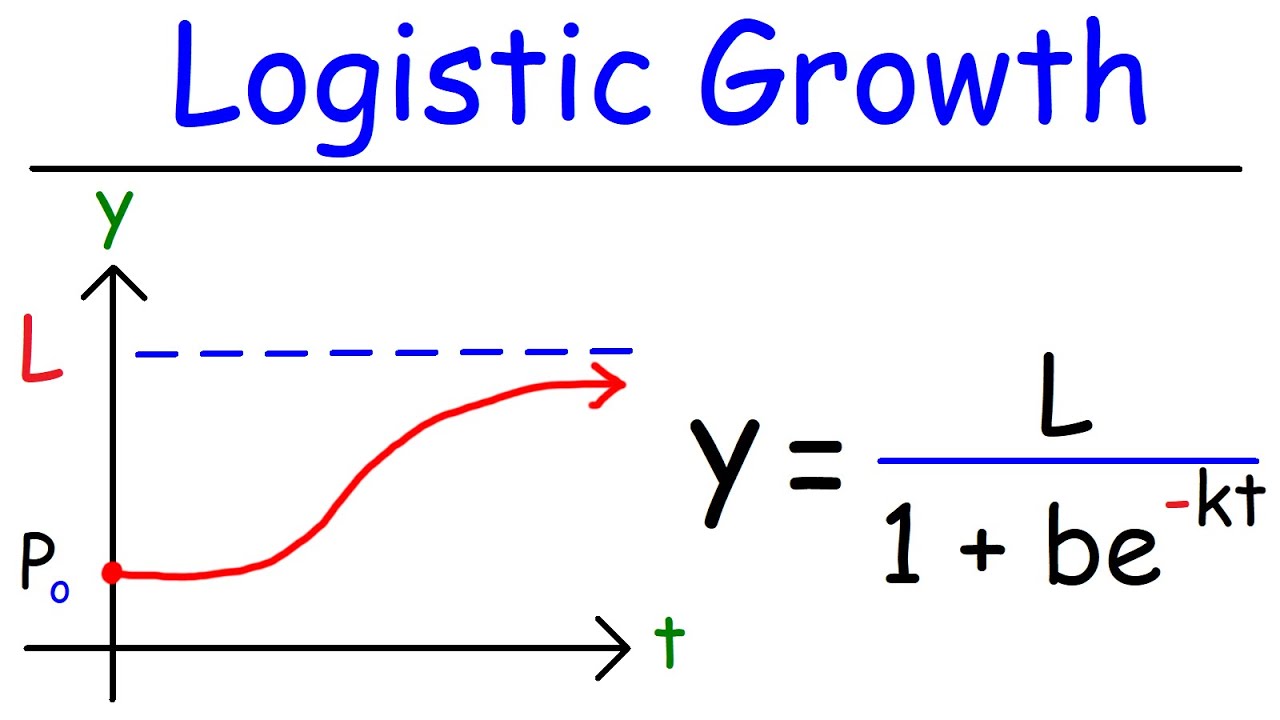
- 🔄 Logistic growth modifies the exponential growth model by including a factor that slows growth as the population approaches the carrying capacity: (K - N) / K.
- 📉 As the population size increases, the logistic growth rate decreases because the factor (K - N) / K becomes smaller, slowing the growth as the population nears K.
- 🌐 At a population size of 100, the logistic growth rate is 18 individuals per year. At 500, it's 50, and at 900, it's 18, showing a significant slowdown as the population grows.
- 🚫 In a logistic growth scenario, the population growth rate cannot exceed the carrying capacity and will asymptotically approach but never reach K.
- 🌉 The logistic growth model provides a more realistic view of population dynamics, accounting for the limitations of finite resources in the environment.
Q & A
What is the per capita growth rate mentioned in the script?
-The per capita growth rate mentioned in the script is 0.2, which indicates that on average, each individual in the population would increase by 20% after one year.
How does the per capita growth rate affect the population size after one year if the initial population is one?
-If the per capita growth rate is 0.2, and the initial population is one, then after one year, the population would increase to 1.2 individuals due to the growth rate.
What is the concept of maximum per capita growth rate in the context of population biology?
-The maximum per capita growth rate is the theoretical growth rate of a population when it is not limited by any environmental factors such as resources, water, food, land, or territory.
How is the exponential growth equation of a population formulated?
-The exponential growth equation is formulated as dN/dt = r * N, where dN/dt represents the rate of change of population with respect to time, r is the maximum per capita growth rate, and N is the population size.
What are the population growth rates when the population is 100, 500, and 900, respectively, using the exponential growth model?
-Using the exponential growth model with a per capita growth rate of 0.2, the population growth rates would be 20 for a population of 100, 100 for a population of 500, and 180 for a population of 900.
What is the concept of carrying capacity in an ecological context?
-The carrying capacity (K) is the maximum population size that an environment can sustain indefinitely, given the food, habitat, water, and other resources available in that environment.
How does the logistic growth model differ from the exponential growth model?
-The logistic growth model differs from the exponential growth model by incorporating a factor that slows down the growth rate as the population size approaches the carrying capacity, ensuring that the population growth does not exceed the environment's limits.
What is the logistic growth equation?
-The logistic growth equation is dN/dt = r * N * (1 - N/K), where r is the maximum per capita growth rate, N is the current population size, and K is the carrying capacity.
How does the logistic growth model reflect the limitations of environmental resources on population growth?
-The logistic growth model reflects the limitations of environmental resources by incorporating a factor (1 - N/K) that reduces the growth rate as the population size (N) approaches the carrying capacity (K), thus preventing unlimited growth.
What happens to the population growth rate as the population size approaches the carrying capacity in the logistic growth model?
-As the population size approaches the carrying capacity in the logistic growth model, the growth rate slows down because the factor (1 - N/K) becomes smaller, eventually approaching zero at the carrying capacity.
How does the logistic growth model compare to the exponential growth model in terms of population growth over time?
-In the logistic growth model, population growth starts similarly to the exponential model but then slows down as the population size increases, eventually stabilizing near the carrying capacity. In contrast, the exponential growth model predicts continuously increasing growth rates without stabilization.
Outlines
📈 Understanding Per Capita Growth Rate and Exponential Growth
The first paragraph introduces the concept of per capita growth rate, denoted by 'r', and explains it with an example where a population's per capita growth rate is 0.2, meaning the population grows by 20% each year. It discusses the distinction between sexual reproduction requiring a male and female, and asexual reproduction where organisms can reproduce independently. The paragraph then defines the maximum per capita growth rate, which assumes no limitations on resources. An exponential growth equation is derived from this concept, where the rate of population change over time is the product of the maximum per capita growth rate and the current population size. The instructor uses a table to illustrate how the population growth rate changes with different population sizes, considering a hypothetical scenario with no environmental limits.
🌿 Logistic Growth and the Carrying Capacity of an Environment
The second paragraph delves into logistic growth, which is a modification of the exponential growth model to account for the carrying capacity of an environment, denoted by 'K'. It explains that as the population size approaches the carrying capacity, the growth rate slows down due to limited resources. The logistic growth formula is introduced, which includes a factor that reduces the growth rate as the population size increases relative to the carrying capacity. The instructor uses a table to demonstrate how the population growth rate is affected at different population sizes, showing a clear reduction in growth rate as the population approaches the carrying capacity. The paragraph concludes with a visual representation of exponential versus logistic growth, highlighting that logistic growth eventually levels off as it approaches the carrying capacity, unlike exponential growth which continues indefinitely.
Mindmap
Keywords
💡Per capita growth rate
💡Exponential growth
💡Maximum per capita growth rate
💡Natural carrying capacity
💡Logistic growth
💡Resource limitation
💡Population dynamics
💡Unfettered growth
💡Biological models
💡Carrying capacity factor
💡Asymptotic growth
Highlights
The concept of per capita growth rate is introduced, denoted by the letter 'r', representing the average growth of a population.
A per capita growth rate of 0.2 implies a 20% increase in population size per individual, annually.
The distinction between sexual reproduction requiring a male and female, and asexual reproduction that can occur without pairing.
The maximum per capita growth rate is defined as the growth rate of a population without any limitations.
The exponential growth equation is formulated as the product of the maximum per capita growth rate and the current population size.
A table is used to illustrate how population growth rate varies with different population sizes.
The natural carrying capacity (K) is introduced as the maximum population size an environment can sustain.
Logistic growth is explained as a modification of exponential growth that includes a factor to slow growth as the population approaches carrying capacity.
The logistic growth equation incorporates a factor that reduces the growth rate as the population size increases towards K.
A visual comparison is made between exponential and logistic growth, showing how logistic growth levels off as it approaches the carrying capacity.
At the carrying capacity, the population growth rate theoretically becomes zero, indicating no further population increase.
The impact of limited resources such as land, food, and water on population growth is discussed.
The concept of asexual reproduction in certain organisms, like budding or dividing in unicellular organisms, is highlighted.
The importance of understanding the per capita growth rate in the context of different types of reproduction is emphasized.
The mathematical representation of population growth is explored through the use of differential equations.
The video challenges viewers to calculate population growth rates at different population sizes, promoting active learning.
The logistic growth model is used to demonstrate how population growth can be modeled more realistically in an ecosystem with limited resources.
The potential consequences of a population reaching its carrying capacity, such as competition for resources and potential starvation, are discussed.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: