Exponential and logistic growth in populations | High school biology | Khan Academy
TLDRThe video script explores the concept of exponential growth using the example of a rabbit population starting with 1,000 individuals growing at a rate of 10% per month. It illustrates how the population would increase over time, reaching approximately 93 million rabbits after 10 years. The script explains that while exponential growth can seem incredibly rapid, it's not unrealistic for species like rabbits when they are not limited by space, food, or predators. However, it also clarifies that in reality, environmental factors such as carrying capacity will eventually limit growth, transitioning the population growth model from exponential to logistic. The logistic growth model is represented by an S-shaped curve, which is more reflective of what happens in nature when environmental constraints are considered. The video also mentions that for a more in-depth understanding, viewers can refer to Khan Academy's resources on logistic and exponential growth.
Takeaways
- 📈 The rabbit population starts with 1,000 and grows at a rate of 10% per month.
- 🔢 The growth can be calculated by multiplying the initial population by 1.1 (10% growth) raised to the power of the number of months.
- 📊 After one month, the population is 1,100 rabbits, which is the initial 1,000 multiplied by 1.1.
- 🔗 The population growth follows an exponential pattern, represented by the formula P = 1,000 * (1.1)^n, where P is the population and n is the number of months.
- 🌟 In 10 years (120 months), the population would theoretically reach approximately 93 million rabbits.
- ⏳ Exponential growth is very fast and can lead to extremely large numbers over time, but it's not unrealistic for species like rabbits under ideal conditions.
- 📉 However, real-world factors like limited food, space, and predators mean that exponential growth cannot continue indefinitely.
- 🌐 There's a maximum carrying capacity for any environment, which is the most population it can sustain without negative consequences.
- 📌 As the population approaches this carrying capacity, the growth rate slows and eventually levels off, following a logistic growth model rather than exponential.
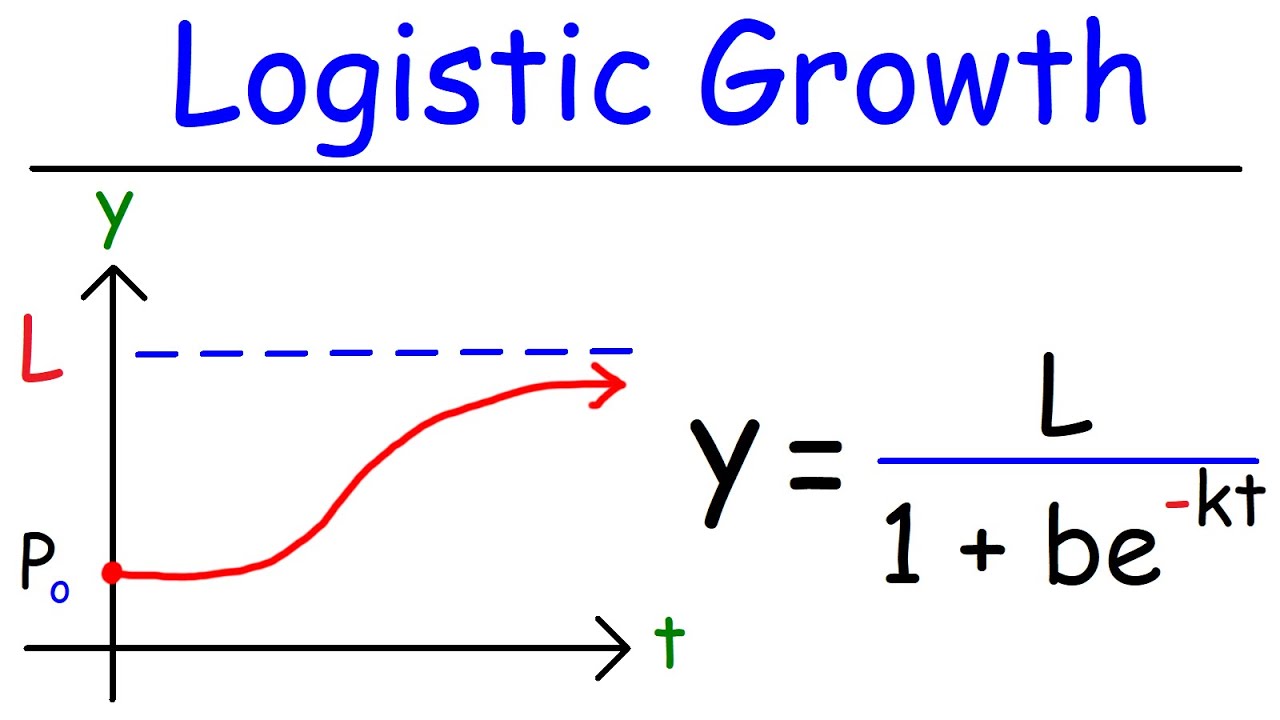
- 📙 The logistic growth model is represented by an S-shaped curve, which is a more accurate representation of population growth in the real world.
- 🔬 For introductory biology, understanding the concepts of exponential and logistic growth is sufficient, with more detailed study available for those interested.
- 🌿 The logistic function and its implications are explored in more depth in resources like Khan Academy for those who want to learn more.
Q & A
What is the initial population of rabbits mentioned in the transcript?
-The initial population of rabbits is 1,000.
At what percentage does the rabbit population grow each month?
-The rabbit population grows at a rate of 10% per month.
How is the growth of the rabbit population calculated?
-The growth of the rabbit population is calculated by multiplying the initial population by 1.1 (which represents a 10% increase) raised to the power of the number of months that have passed.
What is the term for the type of growth described in the transcript?
-The type of growth described in the transcript is known as exponential growth.
What is the population of rabbits after 120 months, according to the transcript?
-After 120 months, the population of rabbits is approximately 93 million.
Why is exponential growth not sustainable in the real world?
-Exponential growth is not sustainable in the real world due to limitations such as finite food, space, and the presence of predators and competition for resources.
What is the term for the maximum number of individuals that an environment can sustain indefinitely?
-The term for the maximum number of individuals an environment can sustain indefinitely is known as the carrying capacity.
What is the shape of the graph that represents exponential growth over time?
-The graph representing exponential growth over time has a 'hockey stick' J-shape, indicating a rapid increase after an initial lag.
What is the alternative model for population growth when the environment's carrying capacity is approached?
-The alternative model for population growth when the environment's carrying capacity is approached is known as logistic growth.
What is the shape of the graph that represents logistic growth?
-The graph representing logistic growth has an S-shaped curve, which asymptotically approaches the carrying capacity.
Why is logistic growth considered a more accurate model for population growth in real-world scenarios?
-Logistic growth is considered a more accurate model for real-world scenarios because it accounts for the carrying capacity of the environment, reflecting the fact that growth cannot continue indefinitely.
How can one find more information about logistic and exponential growth?
-More information about logistic and exponential growth can be found on educational platforms like Khan Academy, which have videos detailing these concepts.
Outlines
📈 Exponential Rabbit Population Growth
The video discusses the concept of exponential growth using the example of a rabbit population starting with 1,000 individuals growing at a rate of 10% per month. The presenter sets up a table to illustrate the growth over time and explains that the population at any given month can be calculated by multiplying the initial population by 1.1 raised to the power of the number of months passed. The video emphasizes the rapid increase in population, demonstrating that after 120 months (10 years), the population would reach approximately 93 million rabbits. It also touches on the unrealistic nature of such growth in real-world conditions due to limitations like space, food, and predators.
🌿 Environmental Carrying Capacity and Logistic Growth
The script moves on to discuss the limitations of exponential growth in natural environments, introducing the concept of carrying capacity. It explains that while exponential growth can be a good model when a population is well below its environmental carrying capacity, it is not sustainable indefinitely. As the population approaches this limit, growth tends to slow and asymptotically approach the carrying capacity, which is better modeled by logistic growth. The video describes logistic growth as an S-shaped curve that levels off as the population reaches the environment's limits. It contrasts this with the straight upward trajectory of exponential growth and suggests that logistic growth is a more accurate model for population dynamics in real-world ecosystems.
Mindmap
Keywords
💡Population Growth
💡Exponential Growth
💡Carrying Capacity
💡Logistic Growth
💡Hockey Stick Curve
💡Resources
💡Predators
💡Competition
💡Environmental Factors
💡Sustainability
💡Modeling
💡Asymptote
Highlights
Starting with a population of 1,000 rabbits growing at 10% per month
Population grows by multiplying the initial population by 1.1 raised to the power of the number of months
After 120 months (10 years), the population would be approximately 93 million rabbits
Exponential growth occurs when a population is not limited by space, predators, or food
The maximum carrying capacity of an environment limits how large a population can grow
As the population approaches the carrying capacity, exponential growth no longer accurately models the growth
The population growth will asymptote towards the carrying capacity but not exceed it
Logistic growth is a better model for population growth once the population approaches the carrying capacity
Logistic growth is described by the logistic function, which produces an S-shaped curve
The logistic function accounts for the carrying capacity and slows population growth as it approaches that limit
Khan Academy has videos that go into more detail on logistic and exponential growth
In reality, factors like limited food and space prevent a population from growing indefinitely
Exponential growth is only a good model for population growth when the population is well below the carrying capacity
As the population grows and resources become scarce, the growth rate will naturally slow down
The hockey stick shape of the exponential growth curve illustrates rapid growth followed by a leveling off
The logistic growth curve more accurately represents how real-world populations grow and stabilize
Logistic growth accounts for environmental factors that limit population size, unlike exponential growth
Modeling population growth is important for understanding and managing natural resources and ecosystems
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: