What is Calculus in Math? Simple Explanation with Examples
TLDRCalculus, a branch of mathematics focusing on minute changes, is explored through an imaginative example of a snail's movement under a magnifying lens. The script explains that calculus is divided into differential and integral calculus, with the former examining the rate of change and the latter accumulating smaller quantities for a comprehensive view. The analogy of a car's speedometer illustrates differential calculus, while the calculation of average speed over a trip represents integral calculus. The historical development of calculus is mentioned, highlighting the contributions of Isaac Newton and Gottfried Leibniz, despite the controversy over their discovery. The script emphasizes the practical applications of calculus in various fields, including medicine, business, economics, and engineering, showcasing its significance in diagnosing diseases, setting payment structures, and making critical structural decisions. Despite its reputation for complexity, calculus is portrayed as an essential tool for understanding and quantifying the world around us.
Takeaways
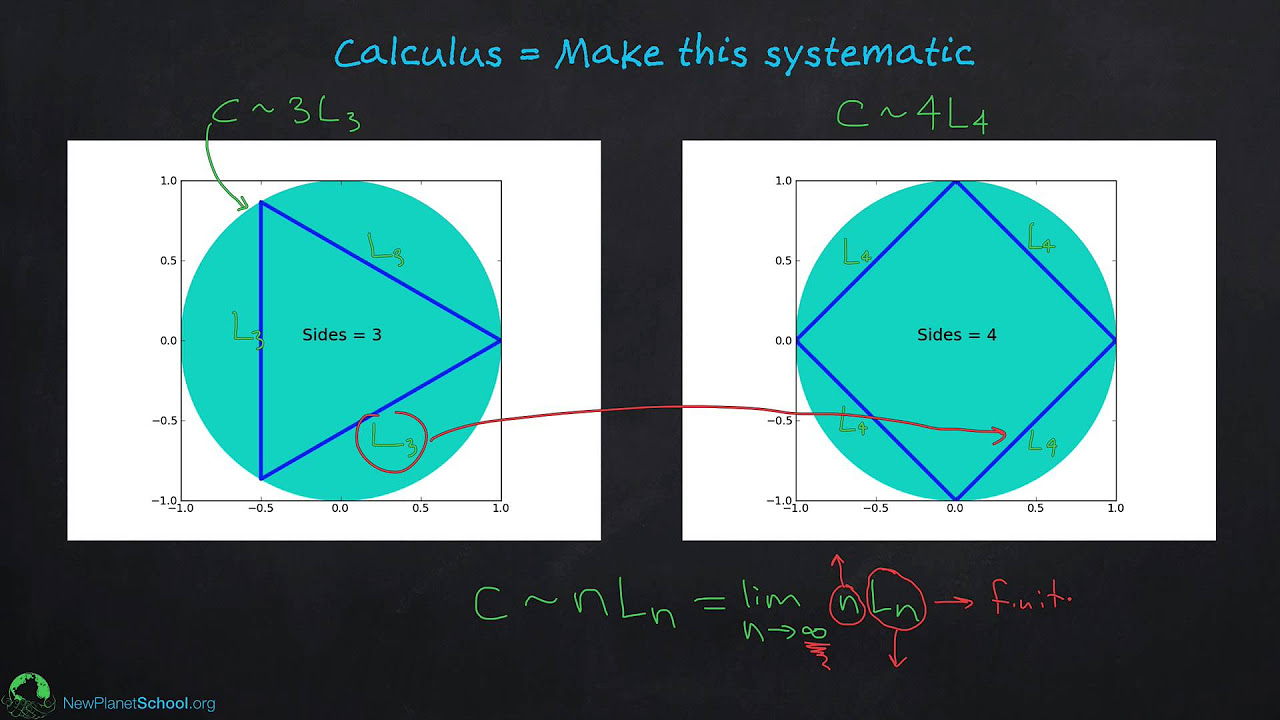
- 📐 **Calculus Definition**: Calculus is the branch of mathematics that deals with small changes and motion.
- 🔍 **Magnifying Lens Analogy**: Calculus allows us to see the small, non-smooth movements that make up what appears to be smooth motion.
- 📈 **Differential Calculus**: This segment focuses on the rate of change, such as speed or the slope of a curve.
- 🧩 **Integral Calculus**: Integral calculus is concerned with the accumulation of small quantities to see the whole picture, like total distance traveled.
- 🚗 **Speedometer Example**: Differential calculus helps determine the speed of a car at a specific instant, whereas integral calculus gives the average speed over a trip.
- 🏆 **Historical Discovery**: Isaac Newton and Gottfried Leibniz are widely recognized for developing calculus, but elements were known to ancient mathematicians.
- 🤝 **Leibniz-Newton Controversy**: There was a significant debate over who discovered calculus first, highlighting the importance of the discovery.
- 🌐 **Applications in Science**: Calculus is used in medical sciences to understand the spread of diseases and the effects of medications.
- 💼 **Business and Economics**: It is essential for setting payment structures in the finance industry and for economic policy-making.
- 🏢 **Engineering Use**: Civil engineers and architects use calculus for critical decisions regarding building design and material selection.
- 📉 **Perception of Difficulty**: Calculus is often seen as challenging, but it provides the tools to measure the complexity of problems, including the 'steepness' of learning curves.
Q & A
What is calculus and what does it deal with?
-Calculus is a branch of mathematics that deals with very small changes and is divided into differential calculus, which primarily deals with the rate of change of things, and integral calculus, which is concerned with the accumulation of smaller quantities to see the 'big picture'.
How does the example of a snail's movement illustrate the concept of calculus?
-The example of a snail's movement illustrates calculus by showing that what appears to be smooth motion is actually a combination of many small, non-smooth movements when viewed through a magnifying lens. This is similar to how calculus examines tiny, moment-by-moment changes.
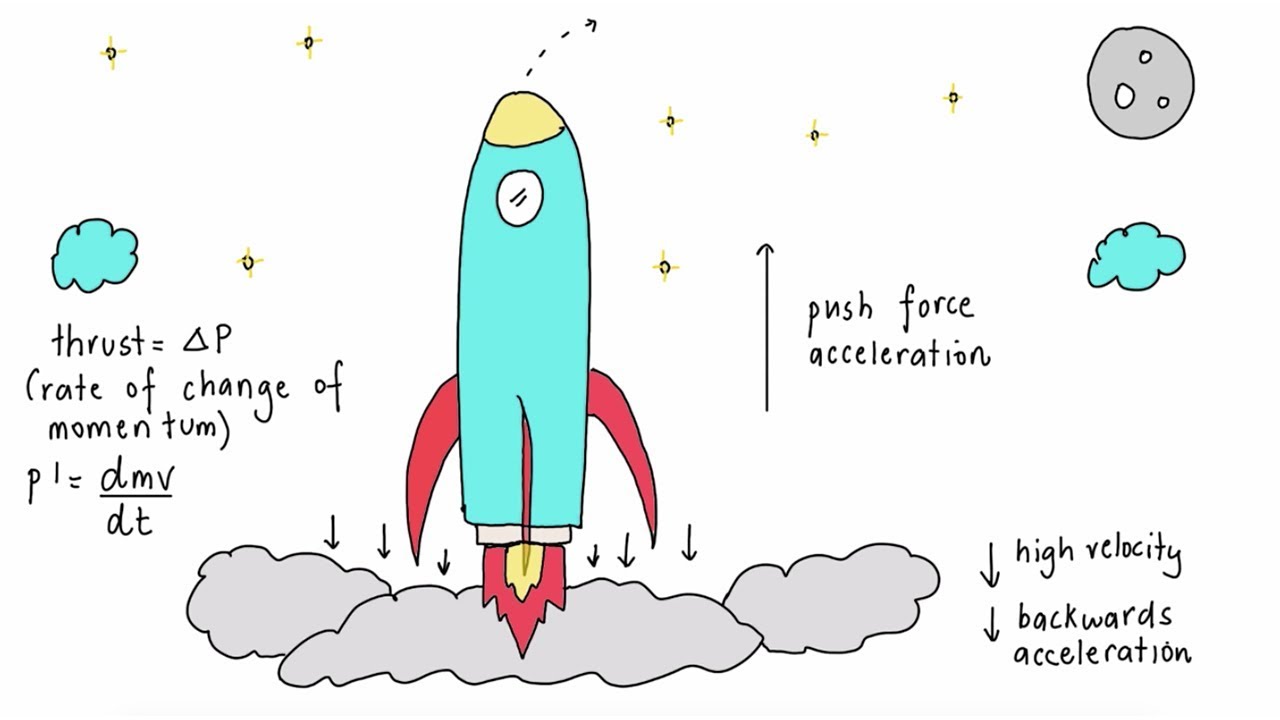
What is the role of differential calculus in understanding the speed of a car?
-Differential calculus allows us to determine the speed of a car at a particular instant during a trip. It's like being able to pause a race and know exactly how fast a car is going at that specific moment.
How does integral calculus differ from differential calculus in its application?
-Integral calculus is used to determine the total distance a car travels throughout an entire trip by putting together small, moment-to-moment snapshots to see the entire picture. It is also used to determine the total size of something, such as area and volume.
Who are the two mathematicians credited with the discovery of calculus, and what is the controversy surrounding their discovery?
-Isaac Newton and Gottfried Leibniz are credited with the discovery of calculus in the late 17th century. The controversy, known as the 'Leibniz-Newton calculus controversy,' revolves around who discovered calculus first, with both mathematicians claiming credit.
How has calculus been applied in medical sciences?
-Calculus is used in medical sciences to diagnose and treat medical conditions. Doctors use it to understand the spread rate of infectious diseases, determine the area where an infection is likely to occur, and compute the side effects of medicine due to minute external factors.
What role does calculus play in business and economics?
-Calculus is essential for business and economics. Credit card companies use it to set payment structures, and policymakers use calculus-based supply-demand graphs to make economic policy decisions.
How is calculus used by civil engineers, architects, and structural engineers?
-These professionals use calculus to make critical decisions regarding the height of buildings and the materials to use in order to withstand natural forces.
Why is calculus often considered difficult to understand by students?
-Calculus is often considered difficult due to its steep learning curve, which involves understanding complex concepts and performing intricate mathematical operations.
What is the historical context of calculus development before Newton and Leibniz?
-Elements of calculus were developed by mathematicians from ancient India, Greece, Egypt, and some Middle Eastern countries many years before Newton and Leibniz claimed credit, indicating that groundbreaking scientific discoveries build upon previous knowledge.
How does the script use the analogy of a race to explain the application of differential calculus?
-The script uses the analogy of a car race where you can hit pause at any time to understand the instantaneous speed of a car, illustrating how differential calculus allows for the examination of moment-by-moment changes.
What is the significance of the 'average speed' concept in the context of the script?
-The concept of 'average speed' is used to contrast with the instantaneous speed, which requires differential calculus. It demonstrates the difference between a general overview (average speed over a trip) and a detailed, precise measurement (instantaneous speed at a specific moment).
Outlines
🔍 Introduction to Calculus
Calculus is introduced as the branch of mathematics that studies very small changes, using the analogy of a magnifying lens to observe a snail's movement. It is divided into differential calculus, which focuses on the rate of change, and integral calculus, which deals with the accumulation of quantities. The example of a car's speedometer is used to illustrate the concept of instantaneous speed versus average speed over a trip. Differential calculus is likened to pausing a race to know a car's exact speed, while integral calculus is needed to calculate the total distance traveled. The segment also touches on the historical development of calculus, mentioning contributions from ancient civilizations and the famous controversy between Isaac Newton and Gottfried Leibniz.
Mindmap
Keywords
💡Calculus
💡Differential Calculus
💡Integral Calculus
💡Rate of Change
💡Accumulation
💡Speedometer
💡Average Speed
💡Slope of a Curve
💡Area and Volume
💡Leibniz-Newton Calculus Controversy
💡Applications of Calculus
Highlights
Calculus deals with very small changes and is divided into differential and integral calculus.
Differential calculus focuses on the rate of change, such as speed and the slope of a curve.
Integral calculus is concerned with the accumulation of smaller quantities to see the 'big picture'.
The speedometer in a car is an example of how calculus can be used to measure instantaneous speed.
Calculating the average speed of a car over a trip is an application of integral calculus.
Differential calculus allows for the precise measurement of speed at any given moment.
Integral calculus is used to determine the total distance traveled by combining small, moment-to-moment changes.
The discovery of calculus is attributed to Isaac Newton and Gottfried Leibniz, but its elements were developed by ancient mathematicians.
The Leibniz-Newton calculus controversy was a significant debate over who discovered calculus first.
Both Newton and Leibniz made unprecedented contributions to the development of calculus.
Calculus is used in medical sciences to diagnose and treat conditions, including the spread of infectious diseases.
Doctors use calculus to compute side effects of medicine influenced by external factors.
Calculus is essential for business and economics, such as setting credit card payment structures.
Policymakers use calculus to make informed economic decisions based on supply-demand graphs.
Civil engineers and architects use calculus for critical decisions regarding building heights and material choices.
Calculus is often considered difficult, but it allows for the precise determination of a curve's steepness.
Calculus has a steep learning curve, but it is an integral part of civilization with countless applications.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: