History of Calculus - Animated

CodeEmporium

28 Oct 201806:43

EducationalLearning

32 Likes 10 Comments

TLDRThis video provides an engaging overview of the history and development of calculus. It highlights the contributions of Isaac Newton and Gottfried Leibniz, who are credited with its foundations, while also exploring the earlier influences from ancient Babylonia, Greece, and medieval India. The video explains key concepts like differential and integral calculus, the method of exhaustion, and the development of infinite series. It underscores that calculus evolved over thousands of years, with significant contributions from various cultures, and continues to be essential in fields like machine learning and AI.

Takeaways

📚 Calculus is the mathematical study of change, encompassing differential calculus for rates of change and integral calculus for quantities like areas and volumes.
🕵️‍♂️ Isaac Newton and Gottfried Leibniz are credited with independently developing the foundational concepts of calculus we use today.
📜 Ancient Babylonians had an early intuition on the infinite process, using a sexagesimal (base 60) number system to represent real numbers with high precision.
📐 In 300 BC, Babylonian astronomers used geometry to study planetary motion, which was foundational to integral calculus.
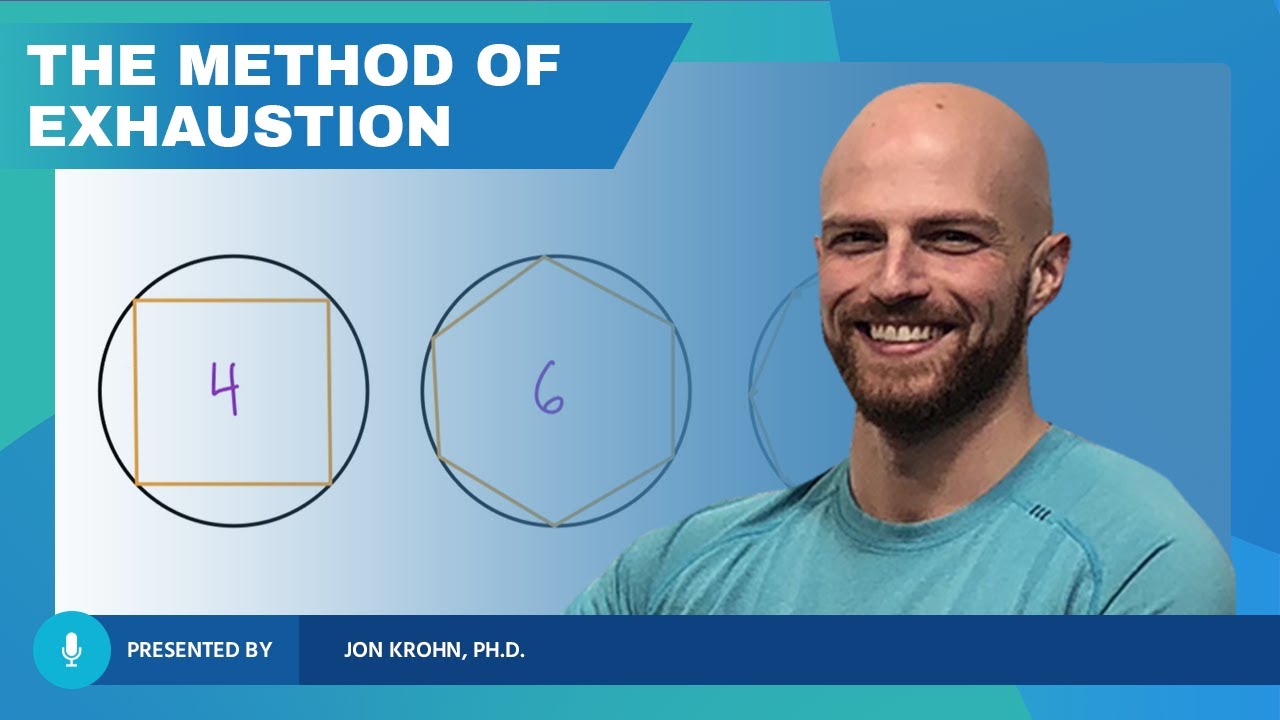
📚 Ancient Greek mathematicians like Eudoxus and Archimedes used the method of exhaustion to calculate areas of shapes, introducing the concept of limits.
🌐 The concept of infinite series was linked with geometry and trigonometry by the Indian mathematician and astronomer Madhava in the 14th century.
🌟 Madhava formulated infinite series expansions for trigonometric functions and pi, known as power series expansions, predating Newton and Leibniz.
📝 Newton's calculus was defined out of necessity for physics, particularly for the laws of motion and gravitation, and was called the method of fluxions.
📘 Leibniz had a more mathematical interpretation of calculus, focusing on sums of infinitesimal distances, which influenced the notation we use today.
🤝 Both Newton and Leibniz are now recognized as co-inventors of calculus, despite initial disputes over who conceived the ideas first.
🚀 Calculus has a rich history with contributions from various cultures and continues to be integral to modern fields such as machine learning and AI.

Q & A

What is the main focus of calculus?
-Calculus is the mathematical study of how things change, focusing on two main branches: differential calculus, which deals with the rate of change using slope as a function, and integral calculus, which is concerned with determining quantities like areas and volumes under changing conditions.
Who are the two individuals credited with the foundations of calculus?
-Isaac Newton and Gottfried Leibniz are the two individuals independently responsible for the foundations of calculus as we know it today.
What is the fundamental theorem of calculus?
-The fundamental theorem of calculus links the concept of differentiation and integration, showing that they are essentially inverse operations.

Outlines

00:00

📚 The Origins and Evolution of Calculus

This paragraph delves into the history of calculus, a branch of mathematics focused on change and motion. It credits Isaac Newton and Gottfried Wilhelm Leibnitz for laying the foundations of modern calculus, but also acknowledges the significant contributions from ancient civilizations like the Babylonians, who developed early concepts of infinite processes and precise measurements. The paragraph highlights the Babylonian sexagesimal number system, their use of clay tablets for recording mathematical observations, and their geometric studies of planetary motion. It also mentions the method of exhaustion used by ancient Greek mathematicians Eudoxus and Archimedes, the contributions of the 12th-century Indian mathematician Bhaskaracharya, and the 14th-century Indian mathematician Madhava, who formulated infinite series expansions for trigonometric functions and pi. The paragraph emphasizes that calculus has a rich and diverse history, with contributions from various cultures and time periods.

05:02

🌐 The Global Development of Calculus and Its Impact

The second paragraph explores the global development of calculus and its impact on modern fields such as machine learning and AI. It discusses how different countries developed their own methods of calculus, with Newton and Leibnitz being key figures who synthesized these methods into a cohesive field. Newton's approach, termed 'method of fluxions,' was rooted in physics and motion, while Leibnitz offered a more mathematical perspective, focusing on sums of infinitesimal distances, which is reflected in the notation we use today. The paragraph also touches on the historical debate over who should be credited with the invention of calculus, noting that both Newton and Leibnitz are now recognized as its co-inventors. The summary concludes by emphasizing the importance of calculus in powering new fields and encouraging viewers to subscribe for more content on data science.

Mindmap

Keywords

💡Calculus

Calculus is the mathematical study of change, encompassing two main branches: differential calculus, which deals with the rate of change and is often represented by the slope of a function, and integral calculus, which is concerned with accumulating quantities such as areas and volumes. In the video, calculus is presented as a foundational tool in understanding the dynamics of the universe, with historical roots tracing back to ancient civilizations and significant contributions from figures like Isaac Newton and Gottfried Leibniz.

💡Differential Calculus

Differential calculus is a subfield of calculus that focuses on the rate at which quantities change. It uses the concept of the derivative to find the slope of a function at a given point, which can be thought of as the instantaneous rate of change. The script mentions differential calculus in the context of using slope as a function to understand how things change over time, such as the motion of planets.

💡Integral Calculus

Integral calculus is concerned with accumulation, summing up small changes to find a total quantity, such as the area under a curve or the volume of a shape. The video script relates integral calculus to the historical practices of the Babylonians, who used a method similar to the trapezoid rule to determine distances traveled by planets, which is analogous to finding areas under curves.

💡Isaac Newton

Isaac Newton is one of the key figures in the development of calculus, known for his work on the laws of motion and universal gravitation. In the script, Newton is humorously referred to as 'the guy behind the laws of cartoons' and is credited with laying the groundwork for calculus, particularly in terms of motion, which he called the 'method of fluxions.'

💡Gottfried Leibniz

Gottfried Leibniz is another foundational figure in calculus, known for his mathematical interpretations and notation that are widely used today. The script contrasts Newton's and Leibniz's approaches, with Leibniz focusing on sums of infinitesimal distances, which aligns with the modern notation for calculus.

💡Babylonians

The Babylonians, from ancient Mesopotamia, contributed to early mathematical concepts that are related to calculus. They had an advanced understanding of the infinite process, as evidenced by their sexagesimal (base 60) number system, which allowed for precise calculations, such as determining the square root of a number to any number of decimal places. The script highlights their use of geometry to study planetary motion, which is foundational to integral calculus.

💡Sexagesimal Number System

The sexagesimal number system, used by the Babylonians, is a base-60 system that enabled them to represent all real numbers using sixty symbols. This system facilitated compact notation and precise calculations, as mentioned in the script when discussing how the Babylonians determined the square root of a rational number to any desired precision.

💡Cuneiforms

Cuneiforms are clay tablets inscribed with cuneiform script, which was used by the Babylonians to record their mathematical research and observations. The script refers to a famous cuneiform that demonstrates the Babylonians' understanding of the relationship between the diagonal of a square and its side, which is a concept related to the Pythagorean theorem.

💡Eudoxus of Cnidus

Eudoxus of Cnidus was an ancient Greek mathematician who contributed to the understanding of areas of shapes through the method of exhaustion. The script mentions his work in proving the areas of polygons, including circles, by inscribing them with polygons and gradually increasing the number of sides, which is a precursor to the concept of limits in calculus.

💡Archimedes

Archimedes, another prominent ancient Greek mathematician, is known for his work on calculating the area and volume of objects using the method of exhaustion. The script refers to his contributions to the understanding of areas of shapes, particularly circles, which is foundational to integral calculus.

💡Bhaskara II

Bhaskara II was a 12th-century Indian mathematician and astronomer who made significant contributions to calculus, including the concept of instantaneous speed of a planet being zero. The script notes that his work was referenced by later Western mathematicians, even though it predates Newton and Leibniz by several centuries.

💡Madhava

Madhava was a 14th-century Indian mathematician who made substantial contributions to the field of calculus by formulating infinite series expansions for trigonometric functions and pi. The script highlights his work on what are now known as power series expansions, which are integral to modern calculus.

Highlights

Calculus is the mathematical study of change, encompassing differential and integral calculus.

Differential calculus focuses on the rate of change using slope as a function.

Integral calculus is concerned with determining quantities like areas and volumes under varying conditions.

Isaac Newton and Gottfried Leibniz are credited with the foundations of calculus.

Calculus has roots dating back to ancient Babylonia, with early intuitions on the infinite process.

Babylonians used a sexagesimal number system, allowing for compact notation of real numbers.

Cuneiform tablets recorded Babylonian mathematical observations, including the value of pi.

Ancient Greek mathematicians like Eudoxus and Archimedes used the method of exhaustion to prove areas of shapes.

The concept of limits and infinite processes was introduced through the method of exhaustion.

12th-century Indian mathematician Bhaskaracharya used calculus in astronomy, predating Newton and Leibniz.

Madhava of 14th-century India formulated infinite series expansions for trigonometric functions and pi.

Madhava's work on infinite series was not widely recognized due to limited documentation.

Newton's calculus, called the method of fluxions, was developed for understanding motion and gravitation.

Leibniz viewed calculus as sums of infinitesimal distances, influencing modern notation.

The credit for calculus is shared between Newton and Leibniz, despite earlier contributions.

Calculus has evolved from multiple roots and continues to influence fields like machine learning and AI.

The history of calculus is complex, with contributions from various cultures and time periods.

Calculus has practical applications.

Transcripts

Browse More Related Video

The Method of Exhaustion – Topic 44 of Machine Learning Foundations

What is Calculus in Math? Simple Explanation with Examples

The Calculus Controversy

Newton versus Leibniz: Who Invented Calculus? - Tony Weathers - April 30, 2015

Newton and Leibniz: Crash Course History of Science #17

Sir Isaac Newton: Unhappy Scientific Genius | Full Documentary | Biography