Inverse Functions

Professor Dave Explains
10 Nov 201706:29
EducationalLearning
32 Likes 10 Comments

TLDRThe video explains the concept of inverse functions in mathematics. It starts by defining inverse functions - if you plug a number into a function and then into the inverse function, you should get back the original number. It then explains how to find the inverse function algebraically - swap the variables X and Y, solve for Y. Some key properties are noted like the domain and range swap between a function and its inverse. Examples are shown step-by-step, like inverting linear and cubic functions. Finally, it's noted graphically that the inverse function reflects the original function over the line y=x.

Takeaways
  • 😀 Inverse functions undo what the original function does. Plugging a number into a function then into its inverse gets you back the original number.
  • 🧮 To find the inverse function, swap f(x) and x in the original equation, then solve for the new f(x).
  • 💡 The domain of the original function equals the range of the inverse function.
  • 📐 Graphing an inverse function reflects the original function over the line y=x.
  • 🔢 Checking f(f-1(x))=x and f-1(f(x))=x verifies inverse functions.
  • 🎯 The inverse reverses the input and output values of all points on the graph.
  • ⛓ Inverse functions systematically undo each step done by the original function.
  • 🔭 Finding inverse functions involves simple algebra like subtracting, dividing, or taking roots.
  • 📈 The domain and range swap places between a function and its inverse.
  • ♾ A function won't have an inverse if you can't solve for f(x) when swapping x and f(x).
Q & A

  • What is the key difference between an inverse function and the reciprocal of a function?

    -The reciprocal of a function is just its output values inverted (1/y), while an inverse function systematically undoes each operation done by the original function. So inverse functions have a specific mathematical relationship, beyond just inverting outputs.

  • If you plug a number into a function and then plug the output into the inverse function, what should you get back?

    -You should get back the original number you plugged into the first function. The inverse function undoes what the original function did.

  • What does it mean when we say the domain of F is equal to the range of F inverse?

    -It means that the set of valid inputs for F becomes the set of possible outputs for F inverse. And vice versa - the outputs of F become the valid inputs for F inverse. The functions essentially swap input and output values.

  • Why do we switch the positions of X and Y when finding an inverse function?

    -We switch them because for an inverse function, the outputs become the inputs and vice versa. So X and Y need to swap positions in the equation to reflect that reversal.

  • What does it mean if you try to find an inverse function but are unable to solve for Y?

    -It means the original function does not have an inverse function. Being able to solve for Y is a requirement for a function to have an invertible inverse.

  • How can graphing inverse functions on the same axes help visualize their relationship?

    -Graphing them shows that inverse functions are reflections across the line y=x. So you can visually see how swapping inputs and outputs makes the functions mirrors of each other.

  • What are some ways you can check that two functions are truly inverses of each other?

    -You can plug one function into the other and see that you get back the original input value. Or you can graph them and see that they are reflections across y=x. Evaluating them at various points is also a good check.

  • If a function is not one-to-one, can it have an inverse function? Why or why not?

    -No, it cannot have an inverse function. For a function to have an inverse, it must pass the horizontal line test - each input must correspond to exactly one output value. Non one-to-one functions fail this test.

  • What is a practical example of using inverse functions in the real world?

    -Inverse functions allow you to undo operations and solve problems working backwards. For example, economists use inverse supply/demand functions to calculate the market effects of price changes.

  • What is one limitation or assumption made when working with inverse functions in math?

    -A key assumption is that the original function must be one-to-one to have an invertible inverse. Many real-world relationships (like squaring numbers) lose one-to-one correspondence and cannot be inverted.

Outlines
00:00
📚 Understanding Inverse Functions

This paragraph explains what inverse functions are, how they undo the operations of the original function. It provides an example of finding the inverse of Y=X+2 by swapping X and Y, then solving for Y to get Y=X-2. It discusses key properties like inverse functions swapping the domain and range. It shows how to prove functions are inverses using composition.

05:05
📐 Using Graphs to Understand Inverse Functions

This paragraph explains how graphing a function and its inverse shows they are reflections across the line Y=X. So graphically, inverse functions simply swap the X and Y coordinates. This visually demonstrates why domain and range are swapped between a function and its inverse.

Mindmap
Keywords
💡Function
A function is a relation between inputs and outputs where each input has a single associated output. In the context of this video on inverse functions, functions are mathematical mappings that take in a number and output some other number.
💡Inverse Function
An inverse function reverses or undoes the operation of the original function. If f(x) is a function, then the inverse function f−1(x) takes the output of f(x) and returns the original input x. A main theme of the video is defining inverse functions and explaining how to find them.
💡Domain and Range
The domain and range describe the set of possible inputs and outputs of a function. As explained in the video, the domain of a function f(x) corresponds to the range of its inverse f−1(x), since the outputs of f(x) become the inputs of f−1(x).
💡Mapping
A function represents a mapping between inputs x and outputs f(x). The video explains that an inverse function reverses this mapping, with f(x) and x switching places.
💡Ordered Pairs
An ordered pair (x, f(x)) represents an input x and its associated output f(x) in a function. For an inverse function, the ordered pairs are reversed as (f(x), x), meaning the outputs become the inputs.
💡Solving for y
The method described in the video for finding inverse functions involves setting y = f(x), switching x and y, and then solving for y. This allows you to express the inverse as a function of x.
💡Reflecting over y = x
Graphically, inverse functions can be formed by reflecting the original function over the line y = x. This switches all (x, y) ordered pairs to (y, x) pairs.
💡Plugging In
As demonstrated in examples, you can check if two functions f(x) and g(x) are inverses by plugging the output of one into the input of the other to see if you get back the original input.
💡Undoes
A key property of inverse functions is that the inverse undoes the operations performed by the original function. So f−1(f(x)) = x, meaning plugging x into f(x) and then into f−1(x) brings you back to the original x.
💡Algebra
As stated in the video, finding inverse functions typically involves simple algebra like switching variables, solving for y, and applying inverse operations (add/subtract, divide/multiply, exponentiate/take roots).
Highlights

Inverse functions undo operations done by the original function

To find the inverse function, swap X and Y variables and solve for Y

If unable to solve for Y after swapping, the function has no inverse

The domain of the original function equals the range of the inverse function

Can check if functions are inverses by composing them to get X back

To get the inverse graph, reflect original function across the line y=x

Finding inverse functions involves simple algebra

Every point XY on the original becomes YX on the inverse

Cubing a function, take cube root of both sides to undo it

Addition is undone by subtracting the same amount

Multiplication is undone by dividing by same factor

Inverses systematically undo each operation done by the original

Can pick value to plug into original and inverse to check if valid

Inverse context different than inverse of a fraction

Use same approach to find inverse function each time

Transcripts

Browse More Related Video

Inverse Functions - Domain & range- With Fractions, Square Roots, & Graphs

Introduction to function inverses | Functions and their graphs | Algebra II | Khan Academy

Function inverse example 1 | Functions and their graphs | Algebra II | Khan Academy

Derivative of Inverse Functions | Calculus 1

Introduction to Inverse Functions

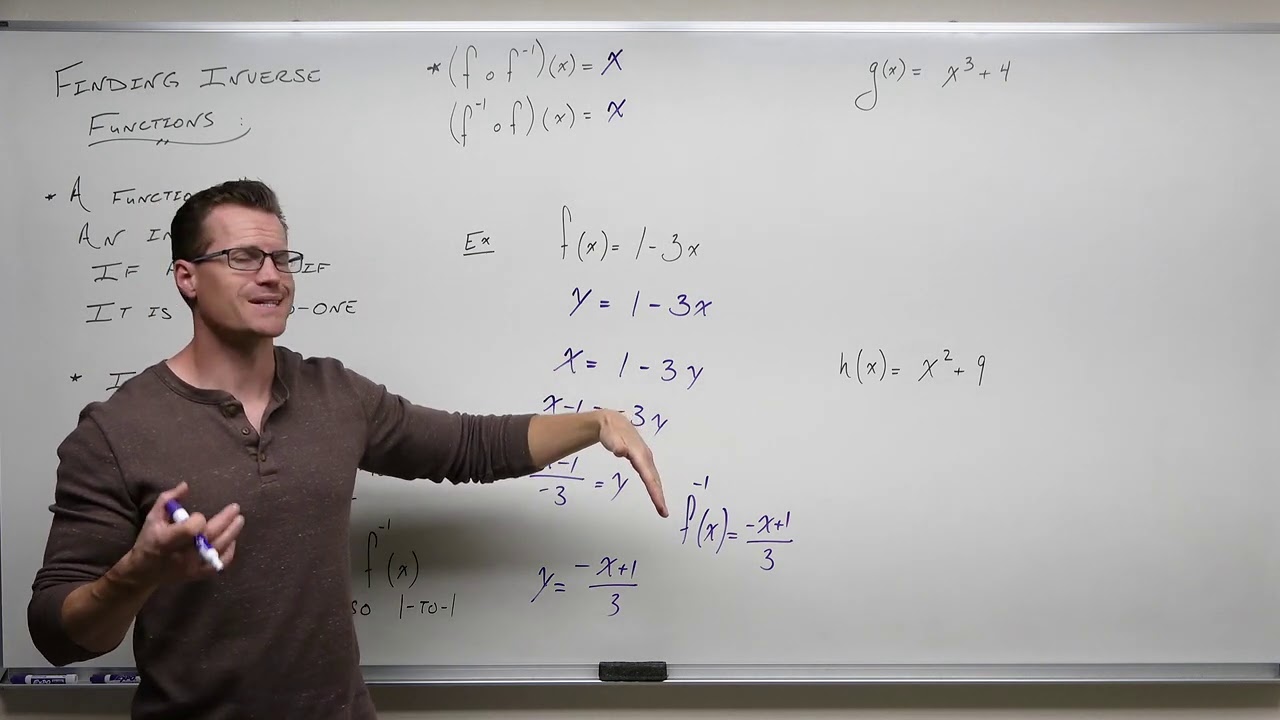
Finding Inverse Functions (Precalculus - College Algebra 51)

Rate This

5.0 / 5 (0 votes)

Thanks for rating: