Three-Dimensional Shapes Part 1: Types, Calculating Surface Area
TLDRThe video introduces polyhedrons, which are three-dimensional shapes with flat polygon faces that meet at edges and vertices. It describes various types of polyhedrons like prisms, cylinders, pyramids, and cones. Formulas are provided to calculate the surface area of these shapes. For example, the surface area of a prism equals the sum of the areas of its rectangular faces, while that of a pyramid equals the area of its base plus the combined area of its triangular faces. The surface areas of basic shapes like spheres and cylinders are also covered. Understanding surface areas of three-dimensional shapes is important as they represent real-world objects.
Takeaways
- ๐ A polyhedron is a 3D shape with flat polygon faces that meet at edges and vertices
- ๐ฏ Prisms have two parallel & congruent polygon bases connected by parallelogram faces
- ๐ Cylinders have two circular bases but are not polyhedra since the faces are not polygons
- ๐บ Pyramids have one polygon base and triangle faces meeting at a point
- โ We can calculate surface area of polyhedra by summing the areas of all their faces
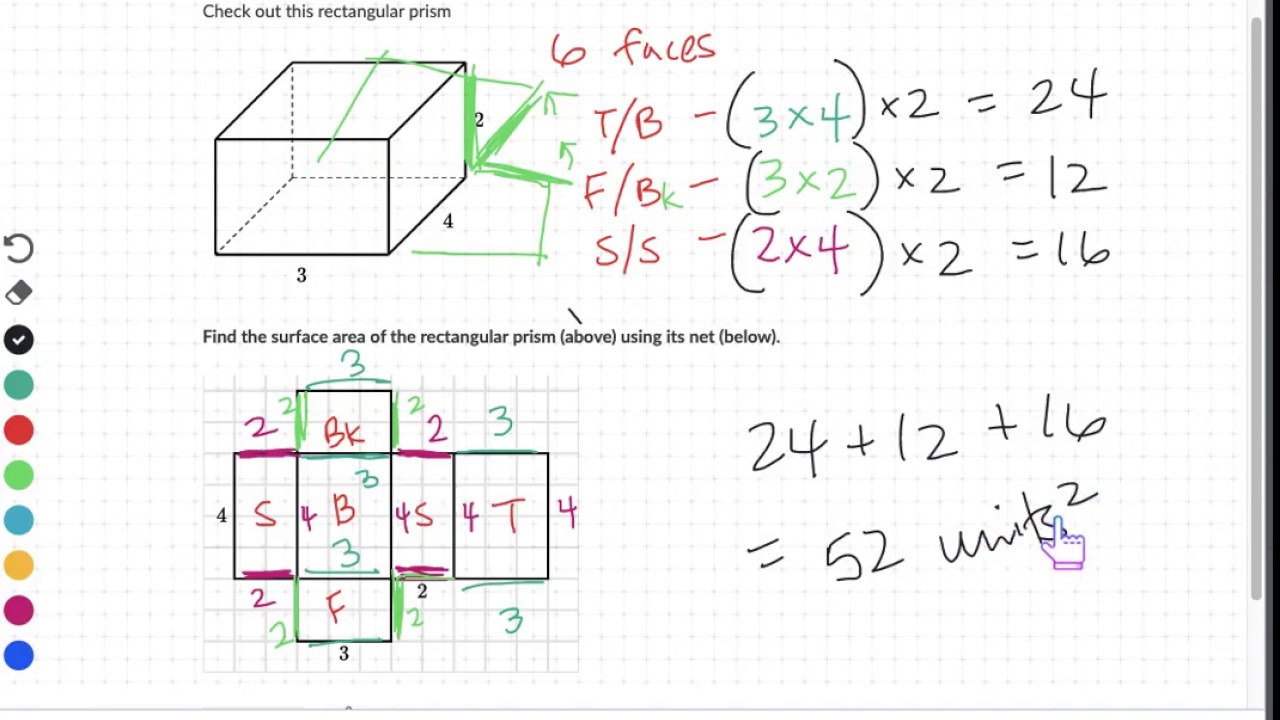
- ๐ The surface area formula for a rectangular prism sums areas of all 6 rectangle faces
- โบ A square pyramid's surface area includes the base plus 4 triangle face areas
- ๐ฏ A cylinder's surface area includes areas of the two circular bases plus a 'wrapped' rectangle
- โก The surface area formula for a sphere with radius R is 4ฯR2
- ๐งฎ Checking comprehension on calculating surface areas of various 3D shapes
Q & A
What is a polyhedron?
-A polyhedron is a three-dimensional object with flat surfaces called faces, where each face is a polygon.
How do prisms differ from pyramids in terms of their bases?
-Prisms have two congruent parallel bases that are polygons, whereas pyramids have only one polygonal base.
Why are cylinders and cones not considered polyhedra?
-Cylinders and cones are not considered polyhedra because their surfaces are not polygons.
How is the surface area of a rectangular prism calculated?
-The surface area of a rectangular prism is calculated by adding up the areas of all its rectangular sides.
What is the surface area formula for a cylinder?
-The surface area of a cylinder is calculated as twice the area of the circle (for the top and bottom) plus the area of the rectangle formed by the side, which is the height times the circumference of the base.
How is the surface area of a sphere calculated?
-The surface area of a sphere is given by the formula 4ฯRยฒ, where R is the radius of the sphere.
What is the significance of calculating the surface area of a 3D shape?
-Calculating the surface area of a 3D shape is important for determining the amount of material needed to cover it, such as wrapping paper for a gift.
What distinguishes a prism named for its base?
-A prism is named after the shape of its bases, such as a rectangular prism for rectangular bases or a hexagonal prism for hexagonal bases.
How do the faces of a pyramid come together?
-In a pyramid, the triangular faces come together at a point, unlike in prisms where the faces are parallelograms connecting two bases.
What is the formula for calculating the surface area of a square pyramid?
-The surface area of a square pyramid is calculated by adding the area of the square base to four times the area of one of the triangles forming its sides.
Outlines
๐ Introducing 3D Shapes and Polyhedrons
This paragraph introduces the concept of 3D shapes or polyhedrons. It defines key properties like faces, edges, vertices. It then introduces some common types of polyhedrons like prisms, pyramids, cones and distinguishes them from cylinders and spheres which are not polyhedrons.
๐ Calculating Surface Area of Polyhedrons
This paragraph explains how to calculate the surface area of different polyhedrons. It provides examples of calculating surface area for a rectangular prism, square pyramid, cylinder and sphere given their dimensions. The formulas highlight using the areas of constituent polygons/circles and accounting for all exposed faces.
Mindmap
Keywords
๐กpolyhedron
๐กsurface area
๐กprism
๐กpyramid
๐กcylinder
๐กsphere
๐กbase
๐กedge
๐กvertex
๐กface
Highlights
A polyhedron is a three-dimensional object with flat surfaces called faces.
Where two faces meet and share a side, this is called an edge.
Any point where three or more edges meet is called a vertex.
A prism is named for the shape of its bases.
Cylinders have two circular bases, but they are not considered polyhedra.
Pyramids have only one base, which is a polygon, and triangles that come together at a point.
We can calculate the total area of all the faces of a polyhedron called the surface area.
Surface area is the amount of wrapping paper needed to wrap a shape.
The area of a cylinder is twice the area of the circle bases plus the area of the curved rectangle.
The surface area of a sphere is 4ฯr^2.
That's quite a lot of shapes and ways to calculate surface area.
Prisms have parallel bases of some polygon connected by parallelograms.
Cones have a circular base and are like pyramids but not polyhedra.
The surface area of a pyramid is the base area plus the areas of the triangles.
Unwrapping a cylinder makes a rectangle with height and circumference.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: