Parametric Equations

Professor Dave Explains
13 Feb 201804:36
EducationalLearning
32 Likes 10 Comments

TLDRThe script discusses parametric equations, where X and Y are calculated separately based on a third parameter T, often time. This is useful for modeling projectile motion, where horizontal and vertical velocities change independently. An example is given using X=2T and Y=T^2. By plugging in T values, plotting points, and eliminating T, we can graph and derive the equation of the resulting parabola. Parametric equations can be easier to visualize or graph, but converting to rectangular coordinates helps connect the approaches. The goal is comprehending translations between coordinate system types.

Takeaways
  • 😀 Parametric equations express X and Y in terms of another variable (usually time)
  • 😲 They are useful for modeling motion, where X and Y change independently
  • 💡 Example is projectile motion, where horizontal and vertical velocities are independent
  • 📏 Set up parametric equations as X=f(T) and Y=g(T) for some parameter T
  • 📊 Plug in values for T to generate x,y coordinate pairs to plot the curve
  • 🔢 Can eliminate the parameter to get a standard equation for the curve too
  • 🖥 Parametric equations can be easier to graph on a calculator
  • 🤔 Choosing between parametric and rectangular depends on the situation
  • ✏️ Key is understanding how to move between the two forms
  • 🧠 Check comprehension on using both types of equations
Q & A

  • What are parametric equations?

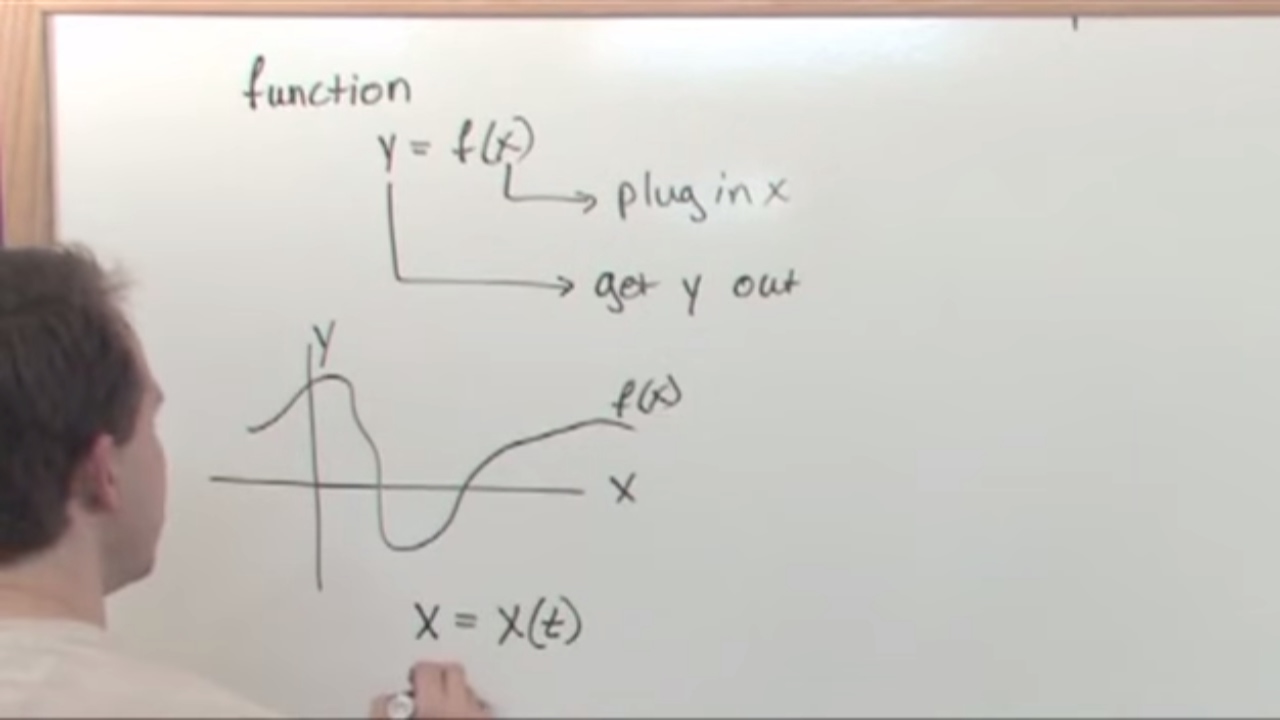
    -Parametric equations are sets of equations in which the X and Y values are calculated in separate equations, and each dependent on some other variable, usually time.

  • Why are parametric equations useful for modeling projectile motion?

    -In projectile motion, the horizontal and vertical positions change independently over time due to constant horizontal velocity and vertically accelerating motion under gravity. Parametric equations allow separate equations for X and Y positions in terms of time.

  • How do you graph a plane curve from a set of parametric equations?

    -Plug in some values for the parameter T, calculate the corresponding X and Y values to get points, plot those points, and connect them to get the curve.

  • What is eliminating the variable in parametric equations?

    -It means solving one parametric equation for the parameter T and substituting it into the other equation to eliminate T and get an equation relating only X and Y.

  • When might parametric equations be easier to use than rectangular equations?

    -Graphing calculators can handle parametric equations for some curves like ellipses more easily. Parametric equations can also be easier when X and Y motion need to be modeled separately.

  • If X = 2T and Y = T^2, what are the parametric equations for the resulting parabola after eliminating T?

    -Solving the first equation for T = X/2 and substituting into the second gives Y = (X/2)^2 = X^2/4. So the single equation is Y = X^2/4.

  • What is the key difference between rectangular and parametric equations of curves?

    -Rectangular equations directly express Y as a function of X. Parametric equations express both X and Y as functions of an independent parameter like time.

  • Why does eliminating the parameter sometimes help in graphing parametric curves?

    -After eliminating the parameter, you have a single equation y=f(x) that can be graphed easily using typical rectangular coordinate methods.

  • What are some examples of real-world applications of parametric equations?

    -Modeling projectile motion, orbits of planets, modeling biological growth rates, mixing chemicals at varying rates, etc. Any system with interdependent variable rates of change.

  • What are the main advantages of the parametric equation representation over rectangular coordinates?

    -The ability to model coupled variable motions separately, ease of graphing some curves, and insight into rate of change relationships between variables.

Outlines
00:00
😀 Introducing Parametric Equations

This paragraph introduces the concept of parametric equations, where X and Y values are calculated separately using different equations that depend on a third parameter T, often representing time. Common applications include modeling projectile motion, where horizontal and vertical velocities change independently. An example is provided using equations X=2T and Y=T^2, which are plotted and then eliminated to find the single equation for the resulting parabola.

Mindmap
Keywords
💡parametric equations
Parametric equations are a set of equations where x and y are calculated separately, each dependent on some other variable (usually time). They are useful for modeling motion where the x and y coordinates change independently over time. For example, the professor discusses using parametric equations to model the motion of a ball that is thrown at an angle - its horizontal velocity is constant while its vertical velocity changes due to gravity.
💡projectile motion
Projectile motion refers to the motion of objects that are given an initial velocity or force and then move under the influence of gravity alone. The professor mentions that parametric equations are commonly used to model projectile motion, as the x and y motion of a launched object like a ball are independent.
💡eliminating the variable
This refers to the process of solving one parametric equation for the parameter (like time) and substituting it into the other parametric equation to get an equation for y in terms of x. The professor shows an example of eliminating time from the sample parametric equations to get the equation of the parabola in rectangular form.
💡graphing calculator
A graphing calculator is a specialized calculator that can graph equations and perform other more advanced mathematical and scientific functions. The professor notes that parametric equations can sometimes be easier to enter and graph on a graphing calculator compared to the equivalent rectangular equation of a shape like an ellipse.
💡ellipse
An ellipse is a type of geometrical shape that looks like an oval. The professor mentions that parametric equations can provide an easier way to define and graph an ellipse on a graphing calculator compared to the standard rectangular equation.
💡parameter
A parameter is a variable in an equation that is kept constant or acts as an arbitrary input to define a family of solutions. In parametric equations, time is usually the parameter that x and y are calculated from.
💡rectangular form
The rectangular or Cartesian form of an equation defines y explicitly as a function of x. By eliminating the parameter from a set of parametric equations, you can find the equivalent rectangular equation. But sometimes the parametric form is more useful.
💡horizontal velocity
Horizontal velocity refers to the rate of change of the x-coordinate over time. The professor explains that when analyzing projectile motion, the horizontal velocity is often treated as constant, while the vertical velocity changes due to gravity.
💡vertical velocity
Vertical velocity refers to the rate of change of the y-coordinate over time. Unlike horizontal velocity, the professor notes that vertical velocity will be accelerating downward due to gravity when analyzing projectile motion.
💡wind resistance
Wind resistance refers to the drag force exerted by air pushing against a moving object. The professor mentions that when modeling projectile motion, wind resistance is often ignored so that the horizontal velocity can be treated as constant.
Highlights

Parametric equations express X and Y in terms of another variable, often time

Parametric equations are useful for modeling projectile motion, where horizontal and vertical velocities change independently

With parametric equations for projectile motion, X position depends on time differently than Y position does

Parametric equations let you model X and Y independently as functions of a parameter like time

To graph parametric equations, make a table of parameter values and plot the corresponding X and Y points

Example parametric equations for a parabola, with parameter T: X=2T, Y=T^2

Can eliminate the parameter to get a regular cartesian equation from parametric equations

Parametric equations can be easier to graph on a calculator compared to cartesian form

Parametric equations are useful for representing some curves, like ellipses

Need to understand both parametric and cartesian forms of equations

X and Y motion in projectiles is independent, so parametric equations make sense

Parametric equations have X and Y as separate functions of a parameter like time

Plot parametric equations by making a table of parameter values and finding X and Y

Can eliminate parameter from parametric equations to get cartesian equation

Parametric equations can simplify graphing some curves on a calculator

Transcripts

Browse More Related Video

Ch. 8.4 Plane Curves and Parametric Equations

AP Calculus BC Lesson 9.1

Parametric equations 3 | Parametric equations and polar coordinates | Precalculus | Khan Academy

Parametric equations 2 | Parametric equations and polar coordinates | Precalculus | Khan Academy

Lesson 10 - Parametric Equations (Calculus 2 Tutor)

Parametric Arclength | MIT 18.01SC Single Variable Calculus, Fall 2010

Rate This

5.0 / 5 (0 votes)

Thanks for rating: