Verifying Trigonometric Identities

Professor Dave Explains
22 Jan 201809:13
EducationalLearning
32 Likes 10 Comments

TLDRThe video explains techniques for verifying trigonometric identities. It starts with simple examples, showing step-by-step how to manipulate expressions using basic trig identities until both sides are equal. More complex examples are tackled later using strategies like rewriting trig functions as fractions, combining fractions, applying trig identities to transform squared functions into 1 or other terms, and more. The narrator emphasizes that while daunting at first, with practice it becomes very satisfying, as you just need to keep trying valid algebraic moves on one or both sides until the identity is proven.

Takeaways
  • 😀 Verifying trig identities involves simplifying equations with trig functions until both sides are equal
  • 👍🏻 Strategies: rewrite trig functions as other identities, combine/split fractions, use Pythagorean identities
  • 🤓 Start by rewriting individual trig functions as other expressions like tangent = sine/cosine
  • 😊 Combine fractions by getting a common denominator if needed to simplify
  • 🔢 Use identities like sine^2 + cosine^2 = 1 strategically to simplify
  • 📐 Split fractions with sums in denominators using conjugates to eliminate the sums
  • ⚙️ Valid strategies include: working with one side, the other side, both sides - whatever makes progress!
  • 🧠 Practice is key to get good at verifying trig identities and using the right strategies
  • ✅ An identity is verified when both sides simplify to the same exact expression
  • 🏁 As long as you make algebraically valid steps, you will likely reach the solution eventually
Q & A

  • What is the purpose of verifying trig identities?

    -The purpose is to simplify trigonometric expressions by repeatedly applying known trig identities until an equivalent expression is reached. This allows you to demonstrate that two seemingly different trig expressions are actually equal.

  • What is the first step to verify a trig identity?

    -The first step is to rewrite any trig functions in the identity using basic definitions. For example, rewrite secant as 1/cosine, tangent as sine/cosine, etc.

  • What trig identity allows you to rewrite sine squared + cosine squared?

    -The trig identity that states: sine squared + cosine squared = 1. This allows you to substitute 1 for sine squared + cosine squared.

  • What are some good strategies when verifying trig identities?

    -Some good strategies include: rewriting trig functions using identities, combining or separating fractions, using trig identities like sine squared + cosine squared = 1, and working algebraically with both sides of the equation.

  • Why multiply cosine x by cosine/cosine in one of the examples?

    -This step is done so that the denominator matches the other fraction, allowing the two fractions to be combined. It does not change the value but sets up for a later step.

  • What is a way to simplify a fraction with a sum or difference in the denominator?

    -Multiply the fraction by a version of the denominator that eliminates the sum/difference through cancellation. This is analogous to using a complex conjugate.

  • What should you do if you get stuck while verifying an identity?

    -Keep trying valid algebraic manipulations on both sides of the equation. Go back and leverage trig identities you know. There are often multiple paths, so persist in exploring workarounds.

  • Why practice verifying trig identities?

    -Practice builds familiarity with strategies and identities, develops persistence, and results in greater ease manipulating trig expressions. More exposure leads to more tricks up your sleeve.

  • When would you need to verify a trig identity in the real world?

    -Trig identities arise frequently in calculus, physics, engineering, and other technical fields. Being able to fluently verify them allows simplification of complex problems into accessible math.

  • What is the key to becoming skilled at verifying trig identities?

    -Repeated practice to build intuition and pattern recognition. Trying many examples trains you to spot productive manipulations. Skills develop through struggling on a volume of identities.

Outlines
00:00
😊 Understanding and Verifying Trig Identities

This paragraph introduces the concept of verifying trig identities. It explains that we can have equations with trig functions on both sides, and we need to simplify the terms by applying identities until both sides are equal. Some strategies are provided, like rewriting individual trig functions, using the sine squared plus cosine squared equals one identity, and combining or splitting fractions.

05:04
😃 Strategies for Verifying Challenging Trig Identities

This paragraph demonstrates strategies for verifying more complex trig identities. It shows how to manipulate fractions by using common denominators or conjugate multiplication. Several examples are worked through, highlighting techniques like expressions trig functions in terms of sines and cosines, combining/separating fractions, and using identities like sine squared plus cosine squared equals one.

Mindmap
Keywords
💡Identities
Refers to equations or relationships between trigonometric functions that are always true. Verifying trig identities involves manipulating expressions with trig functions until both sides are equal, thus proving the identity relationship.
💡Cosecant
The cosecant function, defined as 1/sin(x). It is one of the basic trigonometric functions that appears commonly in trig identity equations.
💡Tangent
The tangent trigonometric function, defined as sin(x)/cos(x). It represents the ratio of the sine and cosine functions and is used frequently in examples of verifying trig identities.
💡Secant
The secant trigonometric function, defined as 1/cos(x). It represents the reciprocal of cosine and is commonly manipulated into equivalent expressions when verifying trig identities.
💡Common denominator
A strategy for combining multiple fractions by finding a denominator that is shared between all the fractions. This allows you to add or equate the numerators.
💡FOIL method
Stands for "First, Outer, Inner, Last" - a process for multiplying two binomial expressions. Used in one example to eliminate a difference in a denominator when verifying an identity.
💡Conjugate
A complex number formed by only changing the sign between the real and imaginary parts. Used similarly as in the video to eliminate a difference between two denominators.
💡Reciprocal
The multiplicative inverse of a number or expression - that is, 1 divided by that value. Used to simplify fractions by multiplying numerators and denominators in verifying identities.
💡Multiple ways
The video emphasizes you can verify identities through different valid algebraic approaches. As long as steps are justified, different pathways can reach the same verified equation.
💡Practice
Doing many examples of verifying trig identities is the best way to improve skills in this area according to the video. Practice helps develop familiarity with strategies.
Highlights

Verifying trig identities involves simplifying equations with trig functions until both sides are equal

Strategies include rewriting trig functions as other identities and using trig function equations like sin^2(x) + cos^2(x) = 1

Combining fractions into one fraction and separating a fraction into multiple fractions are useful techniques

Multiplying a fraction by a complex conjugate is a way to eliminate a difference of terms in the denominator

There are often multiple valid approaches, so persistently applying algebraically sound steps tends to lead to the solution

Expressing complex trig functions as sines and cosines, combining and separating fractions, and using trig identities are key strategies

Practice is the best way to get good at verifying trig identities

1 + tan^2(x) = sec^2(x) can be useful for simplifying some identities

1 + cot^2(x) = csc^2(x) is another handy identity

When there are sums or differences in a denominator, eliminating them can simplify matters

Multiplying fractions by their reciprocal to flip them is a way to quickly simplify some expressions

Don't panic when faced with a messy trig identity - break things down step-by-step

The easiest thing to do is often rewriting individual trig functions as other identities

Clever tricks like multiplying by cosine/cosine can help combine fractions

Identities with squared trig functions are extremely useful for simplifying expressions

Transcripts

Browse More Related Video

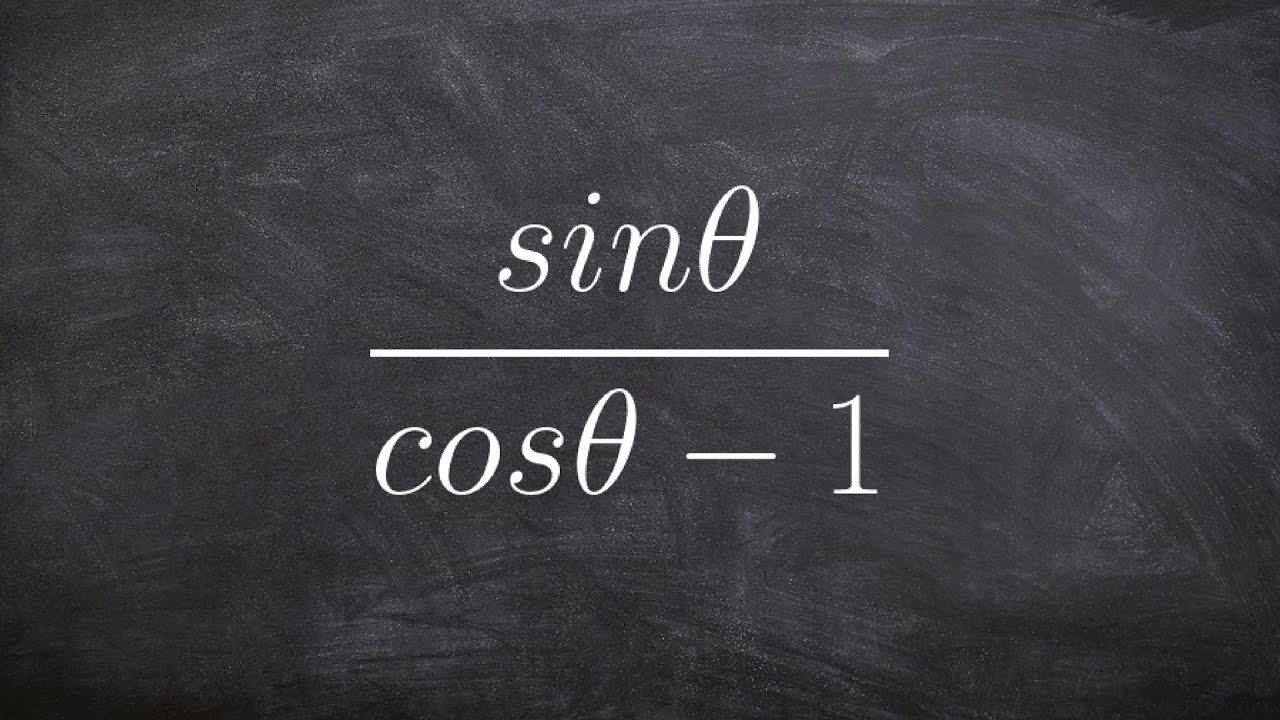
How do you simplify trigonometric expressions

Solving Trigonometric Equations

Ex 2: Simplify Trigonometric Expressions

Proving Trigonometric Identities (Part 2) (5.5)

Reciprocal Identities in Trigonometry (Precalculus - Trigonometry 9)

Basic Trigonometric Identities: Pythagorean Identities and Cofunction Identities

Rate This

5.0 / 5 (0 votes)

Thanks for rating: