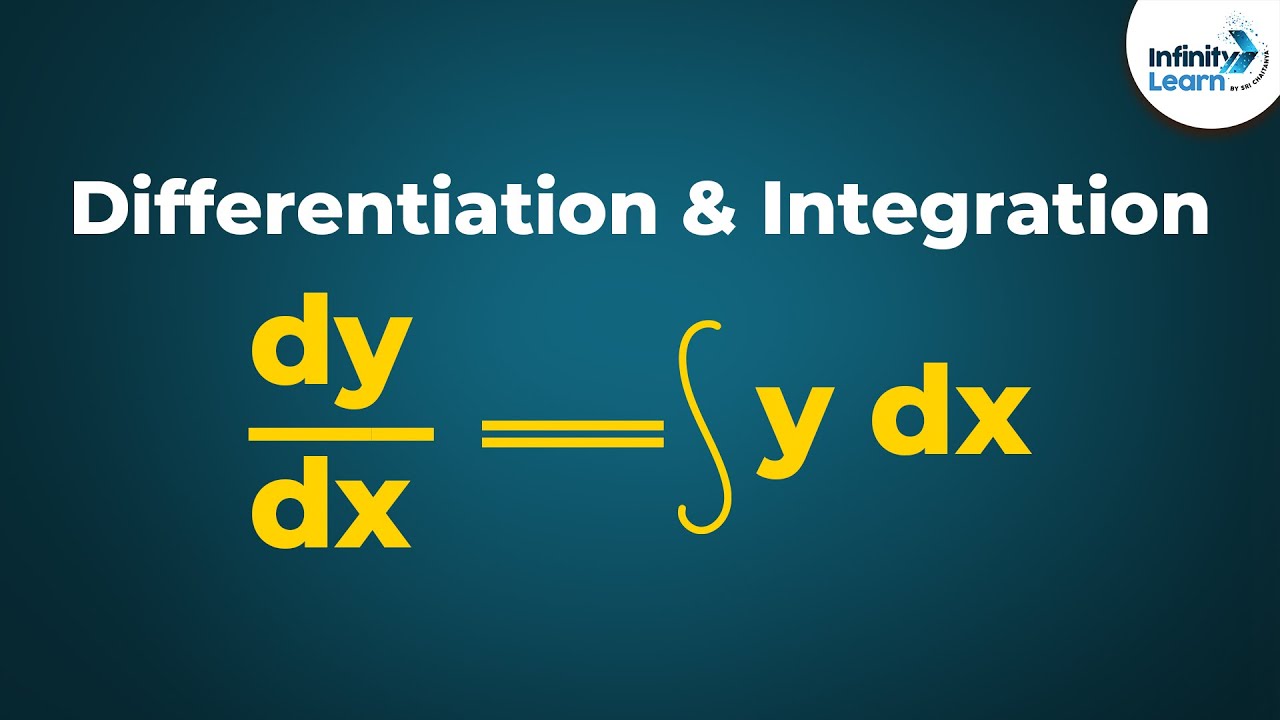Introduction to Calculus: The Greeks, Newton, and Leibniz
TLDRThe video explores the historical origins and mathematical necessity behind the development of calculus. Beginning with the ancient Greeks' attempts to find the area of a circle, it traces the evolution of more and more sophisticated techniques over time. Ultimately Newton and Leibniz formally developed calculus out of a need to describe instantaneous rates of change and finite sums of infinite processes. The video argues that while calculus may seem intimidating, its core concepts involving limits and new operations like differentiation and integration are graspable with diligent study.
Takeaways
- 😲 Calculus was developed out of necessity to solve problems related to areas, velocities, and rates of change that existing math at the time couldn't handle.
- 😎 Newton and Leibniz independently developed calculus in the 17th century, formalizing many of the concepts the Ancient Greeks had begun exploring.
- 📏 Integral calculus focuses on areas under curves, while differential calculus focuses on rates of change and instantaneous velocities.
- 🔢 Calculus involves taking a limit as something approaches infinity - a core paradox since Ancient Greek times.
- 🖥 Newton invented calculus to help understand physics and celestial motion.
- 📈 Finding instantaneous velocities at each moment required new mathematics that eventually became differential calculus.
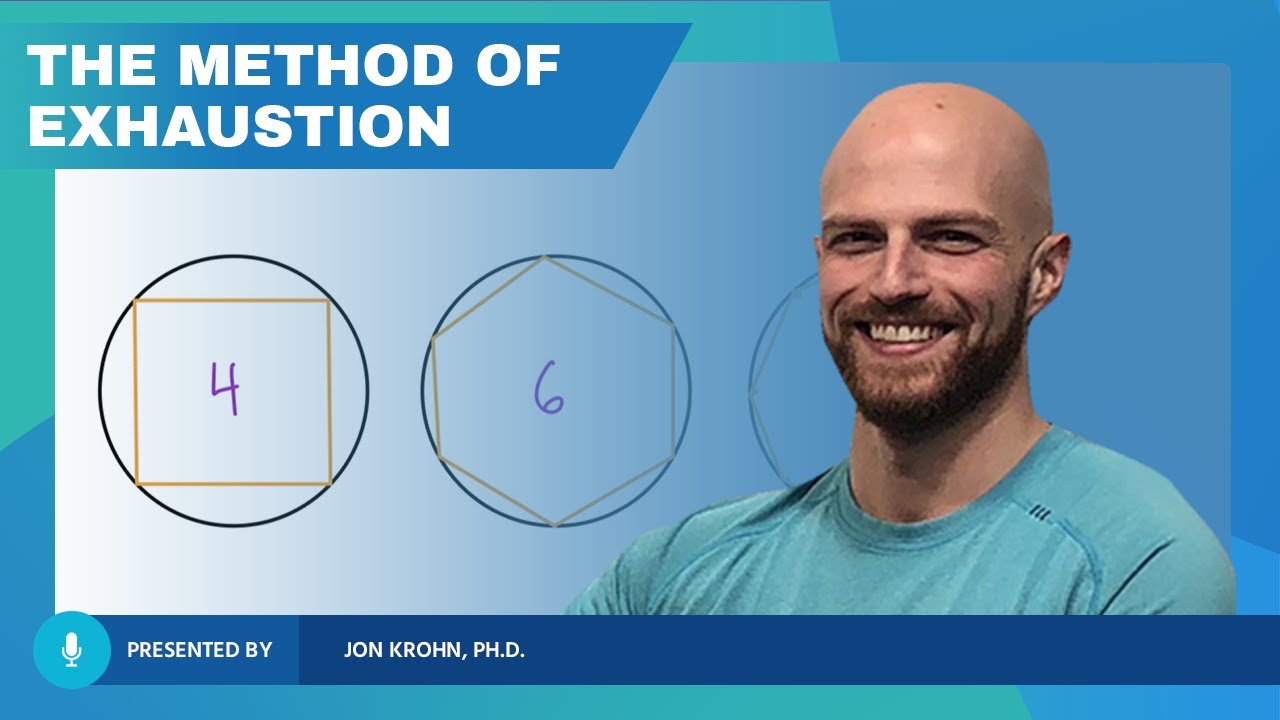
- �prefixlen Rectangle approximation and 'method of exhaustion' were early ideas similar to integral calculus.
- ☑️ Infinite summation series and areas under curves involve doing something infinitely many times but getting a finite, useful answer.
- ⏳ Zeno's paradoxes pondered infinitely dividing distances, foreshadowing modern calculus ideas about limits.
- 🙌 Calculus introduces new operations like differentiation and integration that seem scary at first but just take practice.
Q & A
Why was calculus developed historically?
-Calculus was developed out of the need to calculate areas and volumes of curved shapes, like circles, as well as to analyze rates of change and instantaneous velocities of moving objects. The techniques of geometry and algebra were insufficient for these problems.
How did the ancient Greeks attempt to calculate the area of a circle?
-The Greeks used a method called the method of exhaustion where they would inscribe polygons with more and more sides into a circle. As the number of sides approached infinity, the area of the polygons would get closer and closer to the area of the circle.
Who are credited with developing modern calculus?
-Isaac Newton and Gottfried Leibniz are jointly credited with developing calculus in the 17th century. Newton created concepts needed to solve physics problems regarding motion, while Leibniz systematically developed a notational system still used today.
What is the concept of a limit?
-A limit describes what a function does as the input approaches some value. Limits allow us to evaluate what happens in calculus operations applied infinitely many times, rather than getting stuck in paradoxes about infinity.
What are the two main branches of calculus?
-The two main branches of calculus are differential calculus concerning rates of change, and integral calculus concerning areas under curves.
What does differential calculus allow us to calculate?
-Differential calculus allows us to determine instantaneous rates of change and velocities by calculating the difference between function values versus change in input.
What problem did Isaac Newton have that existing math couldn't solve?
-Newton needed to calculate instantaneous velocities of falling objects, but existing techniques only allowed calculating average velocities over intervals rather than velocities at precise moments.
What are some examples of doing something infinitely many times but getting a finite answer?
-Some infinite series have finite sums, and integrals allow calculating precise area under curves by conceptually using an infinite number of thin rectangles.
What is a paradox that foreshadowed ideas of calculus?
-Zeno's paradox stated that someone could never reach a wall because the remaining distance could be split infinitely many times. This concept of limits resolved this paradox.
What are the major new operations we will learn in calculus?
-The major new operations of calculus are differentiation and integration. Understanding these operations and their associated symbolic notation is key to learning calculus.
Outlines
😊 A Brief History Behind the Origins of Calculus
This paragraph provides background on what necessitated the development of calculus. It starts by explaining how the ancient Greeks struggled to calculate the area of curved shapes like circles using their existing geometric techniques. This led to the method of exhaustion where they would inscribe polygons with more and more sides into the circle to approximate its area. It then explains how a similar logic of drawing rectangles under a curve with more rectangles to better approximate the area is used in integral calculus. The paragraph then transitions to discussing Isaac Newton and Gottfried Leibniz who formally developed calculus out of a need to solve physics problems regarding motion and velocity.
💡 Understanding Instantaneous Velocities and Rates of Change
This paragraph dives deeper into the specific concepts that were not able to be described using existing mathematics, necessitating the development of calculus. It focuses on Newton's exploration of falling bodies, and how he realized that at any instant, the body has a definite velocity, but there was no way to calculate such instantaneous values. This required developing the concept of rate of change and differential calculus. The paragraph then comes full circle, relating this back to the method of exhaustion used by ancient Greeks which illustrated early thinking about doing something infinitely many times to get a useful finite result.
Mindmap
Keywords
💡calculus
💡rate of change
💡area under a curve
💡limits
💡differentiation
💡integration
💡Isaac Newton
💡Gottfried Leibniz
💡physics
💡notation
Highlights
Calculus was developed out of necessity to solve problems in physics regarding celestial motion
Newton and Leibniz independently developed calculus in the 17th century, with Leibniz's notation still used today
Two key ideas of calculus: rates of change (differential calculus) and areas under curves (integral calculus)
Involves doing something infinitely many times to get a useful, finite answer
Related to Zeno's paradoxes about motion and infinity from ancient Greece
Used to find instantaneous velocities and areas of curved shapes
Ancient Greeks developed the method of exhaustion to approximate areas of circles
In the limit as the number of sides approaches infinity, the polygon's area equals the circle's area
Approximate area under curves by sums of narrowing rectangles
No existing math could describe instantaneous rates of change - necessitating calculus
Central idea is determining behavior in the limit as something approaches infinity
Involves new operations like differentiation and integration
Builds on ideas like infinite series and logarithms from previous math studies
Once the operations and symbols are learned, calculus is understandable
Fear of calculus deters students, but with application it can be learned
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: