Solving Trigonometric Equations

Professor Dave Explains

29 Jan 201808:27

EducationalLearning

32 Likes 10 Comments

TLDRThe script provides guidance on solving trigonometric equations, first explaining how to calculate angles of elevation based on triangle dimensions using tangent. It then demonstrates solving basic equations like sine X = 1/2 and more complex quadratic equations using factoring. Other strategies covered include finding solutions on the unit circle, manipulating trig functions directly, and applying trig identities when needed. The overall message is that trigonometric equations can have zero, one, multiple, or infinitely many solutions depending on the form.

Takeaways

😀 Trigonometry allows us to calculate angles and distances in triangles using functions like sine, cosine, and tangent
😎 We can find the angle of elevation of an object by setting up a diagram and using trig ratios
📐 Trig functions relate the sides of a triangle to its angles, enabling calculation of one if we know the others
📏 We can calculate the height of a building if we know the distance away and angle of elevation
🔢 To solve trig equations, we manipulate them algebraically and use inverse trig functions
🌀 Trig equations often have multiple or infinitely many solutions
🖥 Factoring and trig identities can help solve more complex trig equations
❓ Check comprehension on strategies for solving various types of trig equations
✔️ Demonstrated solving linear, quadratic, and more complex trig equations step-by-step
🧮 Trigonometry provides powerful techniques for calculating distances and angles

Q & A

What is the first example problem in the transcript?
-The first example problem is finding the angle of elevation of the sun given that a 30 meter tall building casts a 16 meter long shadow.
What trigonometric function is used to relate the sides of a right triangle to an angle?
-The tangent function relates the sides of a right triangle to an angle.
How can you use trigonometry to calculate the height of a building if you know the distance away and angle of elevation?
-Use the tangent of the angle of elevation, which equals the building height divided by the distance. Then multiply both sides by the distance to solve for the building height.
What does it mean to solve a trigonometric equation?
-Solving a trigonometric equation means finding the value(s) of the variable that satisfy the equation, which often contains trigonometric functions like sine, cosine, and tangent.
Why do trigonometric equations often have multiple or infinitely many solutions?
-Because the trig functions are periodic, repeating their values every 2π radians. So any angle c + 2πn will have the same trig value as c, for any integer n.
What strategy is demonstrated for solving a quadratic trigonometric equation?
-Factoring the quadratic into binomials, setting each binomial equal to 0, and solving each of those simplified trig equations.
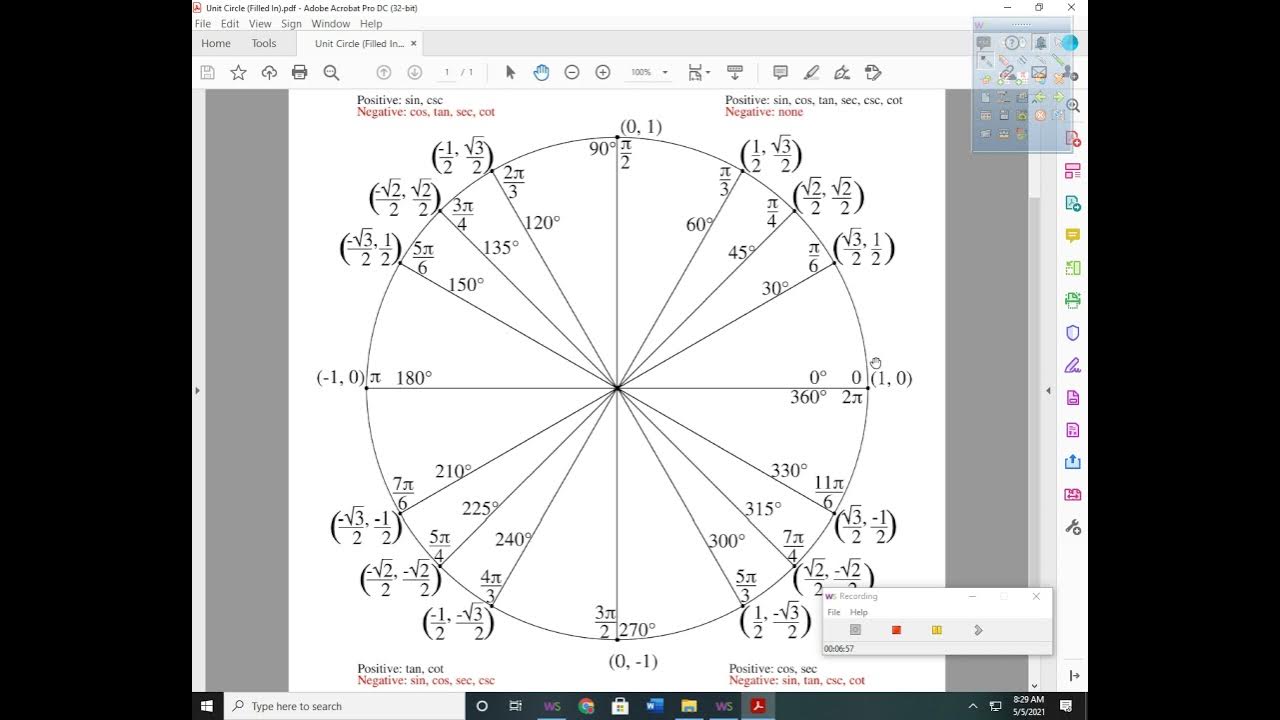
Where in the interval from 0 to 2π does the cosine function equal 1/2?
-The cosine function equals 1/2 at π/3 and 5π/3 in the interval from 0 to 2π.
What trigonometric identities can be used when solving trig equations?
-Trig identities like sin^2(x) + cos^2(x) = 1 can be used to substitute and manipulate the trig expressions while solving equations.
What are some common solutions to trig equations in the interval from 0 to 2π?
-Common solutions are 0, π/2, π, 3π/2, and 2π, as the trig functions take on common values at those points.
What strategies are mentioned for solving trig equations?
-Strategies include: using inverse trig functions, factoring and setting binomials equal to 0, using trig identities, and understanding periodic nature of solutions.

Outlines

00:00

😀 Solving Trigonometric Equations and Word Problems

This paragraph explains how to solve trigonometric equations and apply them to practical word problems. It shows examples of finding the angle of elevation to the sun given the height of a building and length of its shadow. It also demonstrates solving equations with multiple trig function solutions using the unit circle, as well as more complex equations with quadratic and factored forms.

05:02

😀 Using Identities and Other Strategies to Solve Trig Equations

This paragraph discusses additional techniques for solving trigonometric equations over an interval. It shows factoring equations into binomials and using trig identities to manipulate terms. It also explains how sine and cosine values of 0 and π can deduce solutions when factors equal 0.

Mindmap

Keywords

💡trigonometric equations

Trigonometric equations contain trigonometric functions like sine, cosine, tangent, etc. Solving them allows us to find angles or lengths of sides of triangles. The video demonstrates how to solve various types of trigonometric equations using strategies like factoring, inverse trig functions, and trig identities.

💡angle of elevation

The angle of elevation refers to the angle between the horizontal plane and the line of sight to an object above it. In the example, using the tangent function and known heights/distances, the angle of elevation of the sun is calculated to be just under 62 degrees.

💡inverse trig functions

Inverse trig functions allow you to find an angle given a trig ratio. They are used to solve trig equations by taking the inverse function of a known trig ratio to find the angle measure. For example, taking inverse sine of 0.5 gives 30 degrees or π/6.

💡factoring

Factoring involves rewriting an expression as a product of factors. It is used to solve quadratic and other polynomial trig equations. The video shows factoring a quadratic trig equation into binomials and setting each factor equal to 0.

💡trig identities

Trig identities are equality relationships between trig functions that allow you to transform and rewrite expressions. They are useful for solving complex trig equations. The video mentions using identities to transform sine squared and cosine squared terms into each other.

💡unit circle

The unit circle relates trig function values to angle measures in radians. It is used to visualize and determine trig ratios for common angle measures. In the video, it allows finding angles with trig ratios of 0.5 and 1 without a calculator.

💡multiple solutions

Due to the periodic nature of trig functions, trig equations often have multiple valid solutions. The solutions differ by multiples of 2π corresponding to cycles around the unit circle. For example, the solutions for sinX = 0.5 are expressed as π/6 + 2nπ and 5π/6 + 2nπ.

💡interval notation

Interval notation like [0, 2π] specifies the domain over which to solve trig equations. Because trig functions repeat every 2π radians, solutions are only unique within a 2π interval. The video solves several sample equations over the interval from 0 to 2π.

💡radian measure

Radians are used as the angle measure when working with trig functions rather than degrees. The unit circle relations and trig function values rely on radian measures. The video examples emphasize solving trig equations using radian values rather than converting between degrees and radians.

💡trig ratios

Trig ratios refer to the sinusoidal functions sine, cosine, tangent, cotangent, secant, and cosecant. They give ratios between angle measures and side lengths in right triangles. The video shows using tangent, sine, and cosine ratios to relate angles and lengths in applied problems.

Highlights

We can use trigonometry to calculate angles of elevation and building heights based on shadows or distance.

Tangent relates opposite and adjacent side lengths to an angle in a right triangle.

To solve trig equations, we can take inverse trig functions or visualize solutions on the unit circle.

Trig equations can have multiple or infinitely many solutions.

When manipulating trig functions in equations, we may need to account for positive and negative solutions.

Some trig equations take a quadratic form but can still be factored and solved similarly.

The sine and cosine of 0 and π are common solutions for trig equations.

Strategies like factoring and using trig identities help solve complicated trig equations.

Tangent equals 1 at π/4 and 5π/4 due to positive/negative slope ratios.

Cosine equals 1 at 0 and cosine equals 1/2 at π/3 and 5π/3.

Sine equals 0 at 0 and π, useful for factoring trig equations.

Can change sine squared to cosine squared terms using trig identity formulas.

Multiple strategies needed for solving different forms of trig equations.

Trig functions relate triangle side lengths to angles, enabling calculation of unknowns.

Trigonometric equations have wide applications but can be challenging to solve fully.

Transcripts

Browse More Related Video

Solving a trigonometric equation by factoring

Precalc 5.3 Solving Trig Equations

Solving Trigonometric Equations I

How to Solve Basic Inverse Trigonometric Functions (Precalculus - Trigonometry 20)

5.5 Multiple Angle and Product to Sum Formulas (Part 1)

Introduction to Sum and Difference Formulas in Trigonometry (Precalculus - Trigonometry 25)

Solving Trigonometric Equations

Takeaways

Q & A

What is the first example problem in the transcript?

What trigonometric function is used to relate the sides of a right triangle to an angle?

How can you use trigonometry to calculate the height of a building if you know the distance away and angle of elevation?

What does it mean to solve a trigonometric equation?

Why do trigonometric equations often have multiple or infinitely many solutions?

What strategy is demonstrated for solving a quadratic trigonometric equation?

Where in the interval from 0 to 2π does the cosine function equal 1/2?

What trigonometric identities can be used when solving trig equations?

What are some common solutions to trig equations in the interval from 0 to 2π?

What strategies are mentioned for solving trig equations?