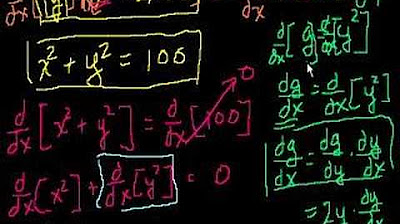Implicit Differentiation

Professor Monte
16 Apr 202107:04
EducationalLearning
32 Likes 10 Comments

TLDRProfessor Manny's video script provides an insightful exploration into the concept of implicit differentiation, a method used to find derivatives of equations that are not explicitly in terms of x. The script begins with a basic example of differentiating an equation with respect to x, highlighting the use of the chain rule when dealing with variables other than x. It then delves into implicit differentiation, emphasizing the importance of treating y as a function and applying the chain rule accordingly. The video offers two examples: differentiating the equation of a circle and a more complex equation involving x and y. Each example demonstrates the process of taking derivatives implicitly, showing how to isolate and solve for dy/dx. The key takeaway is that when differentiating with respect to x, treat x normally but use the chain rule for y, factor out dy/dx when necessary, and simplify the expression. The script encourages practice to master the technique, and ends with a call to action for viewers to like and subscribe for more educational content.

Takeaways
  • 📚 Implicit differentiation is used when you can't express y in terms of x directly.
  • 🔑 The chain rule is crucial in implicit differentiation, especially when dealing with y as a function of x.
  • 📈 When differentiating with respect to x, if the expression is just x, the derivative is straightforward.
  • 📉 If the expression involves y (a function of x), use the chain rule and multiply by dy/dx.
  • 🔍 In implicit differentiation, you take the derivative of both sides of the equation with respect to x.
  • 🧩 For terms involving both x and y, use the product rule to find their derivatives.
  • 🌀 Isolate and factor out dy/dx terms to simplify the resulting equation.
  • ⚖️ The goal is to express dy/dx in terms of x and y, without explicitly solving for y.
  • 🔢 Practice is key to mastering implicit differentiation, as it can be a complex concept.
  • 📐 Examples provided in the script demonstrate the process of differentiating equations like x^2 + y^2 = 25 and x^2 + 3xy = 5y^2.
  • 📝 Implicit differentiation is particularly useful when the equation does not easily allow for explicit expression of y in terms of x.
Q & A

  • What is implicit differentiation?

    -Implicit differentiation is a method used to find the derivative of an equation when it is not explicitly expressed in terms of one variable. It involves differentiating both sides of an equation with respect to a variable, typically 'x', and then solving for the derivative of the function 'y' with respect to 'x'.

  • Why is the chain rule used in implicit differentiation?

    -The chain rule is used in implicit differentiation because when differentiating a term that involves 'y', which is a function of 'x', we need to account for the rate of change of 'y' with respect to 'x'. This is done by multiplying the derivative of the term inside by 'dy/dx'.

  • How do you differentiate the term '8x + 2' with respect to 'x' using implicit differentiation?

    -In implicit differentiation, you would treat '8x + 2' as 'y', which is a function of 'x'. The derivative would then be '4y^3 * dy/dx' for 'y^4', and '8 * dy/dx' for '8x', since the derivative of 'x' with respect to 'x' is '1'.

  • What is the derivative of x^2 + y^2 = 25 with respect to x using implicit differentiation?

    -The derivative is found by differentiating both sides with respect to 'x'. This gives '2x + 2y * dy/dx = 0'. After rearranging, we get 'dy/dx = -x/y'.

  • In the equation x^2 + 3xy = 5y^2, how do you handle the term '3xy' when differentiating with respect to x?

    -The term '3xy' involves both 'x' and 'y', so you use the product rule. The derivative of '3xy' with respect to 'x' is '3y + 3x * dy/dx'.

  • What is the final form of the derivative for the equation x^2 + 3xy = 5y^2 after using implicit differentiation?

    -After rearranging and factoring out 'dy/dx', the final form of the derivative is '(2x + 3y) / (10y - 3x)'.

  • What is the key to solving problems using implicit differentiation?

    -The key is to differentiate with respect to 'x'. For terms involving only 'x', use the standard derivative. For terms involving 'y', apply the chain rule and multiply by 'dy/dx'. If there are multiple 'dy/dx' terms, get them on the same side, factor them out, and then simplify the equation.

  • Why might you not solve for 'y' explicitly in an implicit differentiation problem?

    -You might not solve for 'y' explicitly because it may not be possible to express 'y' in terms of 'x' in a simple or useful way. Implicit differentiation allows you to find the derivative of 'y' with respect to 'x' without needing to isolate 'y'.

  • How does practice help in understanding implicit differentiation?

    -Practice helps in understanding implicit differentiation by reinforcing the method's steps and allowing you to become familiar with the various forms and structures of equations that can be differentiated implicitly.

  • What is the role of 'dy/dx' in implicit differentiation?

    -'dy/dx' represents the derivative of 'y' with respect to 'x'. It is used to denote the rate of change of the function 'y' as 'x' changes, which is crucial when differentiating terms involving 'y'.

  • Can implicit differentiation be used for any equation involving 'y' as a function of 'x'?

    -Implicit differentiation can be used for any equation where 'y' is a function of 'x', especially when it is not straightforward or possible to express 'y' explicitly in terms of 'x'.

  • What is the general approach to solving an equation using implicit differentiation?

    -The general approach involves differentiating both sides of the given equation with respect to 'x', treating 'y' as a function of 'x', and then solving for 'dy/dx', which represents the derivative of 'y' with respect to 'x'.

Outlines
00:00
📚 Introduction to Implicit Differentiation

Professor Manny introduces the concept of implicit differentiation, explaining how it differs from explicit differentiation. He uses an example involving a function of 'y' in terms of 'x' and demonstrates the need to apply the chain rule when differentiating with respect to 'x'. The key insight is that while the derivative of 'x' is straightforward, the derivative of 'y' requires multiplying by the derivative of 'y' with respect to 'x', denoted as dy/dx. The professor then illustrates this with a simple example of a circle's equation, x^2 + y^2 = 25, and shows how to rearrange terms to solve for dy/dx.

05:01
🔍 Applying Implicit Differentiation to a More Complex Problem

The professor moves on to a more complex example, x^2 + 3xy = 5y^2, to further illustrate the process of implicit differentiation. He explains the use of the product rule for terms involving both 'x' and 'y', and emphasizes the strategy of gathering all dy/dx terms on one side to facilitate factorization. The goal is to isolate and solve for dy/dx. The professor concludes by reminding viewers of the importance of practice in mastering implicit differentiation and encourages them to like and subscribe for more educational content.

Mindmap
Keywords
💡Implicit Differentiation
Implicit differentiation is a method used in calculus to find the derivative of an equation that does not explicitly express one variable in terms of another. It is central to the video's theme, as the professor uses it to solve equations where 'y' is not isolated. For example, in the equation 'x^2 + y^2 = 25', the professor differentiates both sides with respect to 'x', applying the chain rule to 'y^2' to get '2y * dy/dx'.
💡Chain Rule
The chain rule is a fundamental principle in calculus for differentiating composite functions. It states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function. In the context of the video, the chain rule is used when differentiating 'y' terms, as seen when differentiating '8x + 2' represented as 'y', resulting in '4y^3 * dy/dx'.
💡Derivative
A derivative in calculus represents the rate at which a quantity changes with respect to another quantity. It is a key concept in the video, as the professor demonstrates how to find derivatives of equations using implicit differentiation. For instance, the derivative of '5x' with respect to 'x' is simply '5', as stated by the professor.
💡Product Rule
The product rule is a formula used to find the derivative of a product of two functions. It is used in the video when the professor encounters the term '3xy', which requires differentiating both '3x' and 'y' separately and then combining them. The rule is expressed as (fg)' = f'g + fg', and in the script, it is applied to get '3x * (1) + 3 * dy/dx'.
💡dy/dx
The notation 'dy/dx' represents the derivative of 'y' with respect to 'x'. It is a recurring concept in the video, used to denote the rate of change of 'y' as 'x' changes. The professor emphasizes that when differentiating 'y' terms, one must multiply by 'dy/dx', as seen when differentiating 'y^4' to get '4y^3 * dy/dx'.
💡Variable
In mathematics, a variable is a symbol that represents a quantity that can change or vary. In the video, 'x' and 'y' are used as variables in the equations. The professor explains that when differentiating with respect to 'x', one must consider 'y' as a function of 'x', denoted by 'dy/dx', which is crucial for implicit differentiation.
💡Function
A function in mathematics is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. In the context of the video, 'y' stands for a function of 'x', which may not be explicitly solvable but is represented in the equations. The concept is central to understanding how implicit differentiation deals with 'y' as a dependent variable.
💡Constant
A constant is a value that does not change its value in a given context. In the video, when the professor differentiates the equation 'x^2 + y^2 = 25', the constant '25' remains unchanged when taking the derivative, resulting in '0', as constants differentiate to zero.
💡Simplify
Simplifying an equation or expression means to reduce it to a more straightforward or standard form. The professor demonstrates simplification when he reduces '2x + 3y * dy/dx' by dividing both sides by '2y', resulting in '-x/y'. Simplification is a common step in solving differential equations.
💡Practice
Practice is the act of performing or rehearsing an activity to improve or maintain one's skill in it. The professor emphasizes the importance of practice in understanding and mastering implicit differentiation, as it is a less intuitive method compared to explicit differentiation.
💡Composite Functions
Composite functions are functions that are made by combining two or more functions. In the video, when the professor differentiates 'y' represented as '8x + 2', it is treated as a composite function, which is why the chain rule is applied to find its derivative.
Highlights

Introduction to implicit differentiation and its derivation process.

Explanation of using the chain rule when differentiating with respect to x.

Differentiating an equation where y is not explicitly in terms of x.

The concept of treating y as a function and using dy/dx in the differentiation process.

Demonstration of implicit differentiation on a simple equation: x^2 + y^2 = 25.

Technique to isolate dy/dx and simplify the derivative expression.

Approach to a more complex equation: x^2 + 3xy = 5y^2.

Use of the product rule in implicit differentiation for terms involving both x and y.

Strategy to get all dy/dx terms on the same side of the equation.

Factoring out dy/dx to simplify the equation and solve for it.

Final step of dividing by the coefficient to isolate dy/dx.

Emphasis on the importance of practice to master implicit differentiation.

Encouragement for viewers to like and subscribe for more educational content.

Summary of the key steps in implicit differentiation: normal differentiation for x, and chain rule application for y.

Explanation of how to handle multiple dy/dx terms in an equation.

The process of moving towards a final simplified form of the derivative.

Advice on how to approach and solve implicit differentiation problems effectively.

The significance of understanding the underlying principles of implicit differentiation for problem-solving.

Transcripts

Browse More Related Video

Implicit Differentiation

Implicit Differentiation Method

Implicit Differentiation for Calculus - More Examples, #1

Implicit Differentiation

Math 11 - Section 3.8

Implicit Differentiation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Implicit DifferentiationMathematicsDerivativesEducationChain RuleProduct RuleProfessor MannyLearningCalculusEducational ContentMath Tutorial