Universal Gravitational Potential Energy Introduction

Flipping Physics
4 Feb 201808:46
EducationalLearning
32 Likes 10 Comments

TLDRThe video script introduces the concept of universal gravitational potential energy, differentiating it from the standard gravitational potential energy equation. It explains that universal gravitational potential energy is always negative and is given by the equation involving the universal gravitational constant, masses of two objects, and the distance between their centers of mass. The script emphasizes the importance of the negative sign, the requirement of two objects for gravitational potential energy, and the absence of squaring the distance variable 'r' in this equation. The video also draws parallels and distinctions between universal gravitational potential energy and Newton's Universal Law of Gravitation.

Takeaways
  • 📚 Gravitational potential energy is the product of an object's mass, acceleration due to gravity (g), and its height (h) above a chosen reference level.
  • 🌍 The standard equation for gravitational potential energy is applicable when the object is on the surface of a planet and the gravitational field is constant.
  • 🌐 Universal Gravitational Potential Energy is represented by the equation U = -(G * m1 * m2) / r, where G is the universal gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between their centers of mass.
  • 🔄 Newton's Universal Law of Gravitation and the equation for Universal Gravitational Potential Energy are similar but not identical; the latter is always negative and does not have a squared term for the distance (r).
  • 📈 The negative sign in the Universal Gravitational Potential Energy equation is due to the chosen zero point, which is at infinite separation between two objects.
  • 🚀 When an object is on the surface of a planet, the Universal Gravitational Potential Energy can be related to the standard gravitational potential energy equation by substituting the expression for gravitational acceleration (g) derived from the universal constant and the planet's radius.
  • 🌌 The concept of Universal Gravitational Potential Energy is useful for understanding interactions between any two objects, not just those near the Earth's surface.
  • 📊 A graph of Universal Gravitational Potential Energy versus the distance between two objects shows a concave downward curve, indicating that potential energy decreases as the distance increases.
  • 🔴 It is crucial to remember the negative sign when using the equation for Universal Gravitational Potential Energy, as it is often forgotten.
  • 🔵 Gravitational potential energy requires two objects and cannot exist with just a single object in isolation.
  • 🔢 The variable 'r' should not be squared in the calculation of Universal Gravitational Potential Energy, which is a common mistake made by students who might erroneously include it based on familiarity with Newton's Law of Gravitation.
Q & A

  • What is the formula for gravitational potential energy in a constant gravitational field?

    -The formula for gravitational potential energy in a constant gravitational field is given by PE = mgh, where m is the mass of the object, g is the acceleration due to gravity, and h is the vertical height above the reference zero level.

  • How do you determine the location of the zero level for gravitational potential energy?

    -The location of the zero level for gravitational potential energy is determined by the specific problem or context. It is the point where the potential energy is considered to be zero, often chosen as the reference level where the object is at a certain distance from the influencing body, such as on the surface of a planet.

  • What is the significance of the negative sign in the equation for universal gravitational potential energy?

    -The negative sign in the equation for universal gravitational potential energy indicates that the potential energy is always negative when the objects are closer than infinity. This is because the zero point of potential energy is defined at an infinite distance between two objects, where the potential energy is zero.

  • How does the value of the universal gravitational constant (G) affect the calculation of potential energy?

    -The universal gravitational constant (G) is a factor in the equation for universal gravitational potential energy, which is given by U = -G * (m1 * m2) / r. A larger (or smaller) value of G would result in a proportionally larger (or smaller) value of potential energy between two objects.

  • What is the relationship between the universal gravitational potential energy and Newton's Universal Law of Gravitation?

    -While the equation for universal gravitational potential energy is similar in form to Newton's Universal Law of Gravitation, they are not the same. Newton's Law provides the force of gravity between two masses, whereas the potential energy equation provides the energy associated with the gravitational force.

  • Why is it important to remember that universal gravitational potential energy requires two objects?

    -It is important because potential energy arises from the interaction between two objects, not from a single object in isolation. This means that to calculate gravitational potential energy, one must consider both the object of interest and the other influencing body, such as the Earth.

  • What is the significance of the distance 'r' in the universal gravitational potential energy equation?

    -The distance 'r' represents the distance between the centers of mass of the two objects. It is crucial in determining the magnitude of the gravitational potential energy, as the potential energy is inversely proportional to the distance between the objects.

  • How does the potential energy change when an object is brought closer to the Earth's surface?

    -As an object is brought closer to the Earth's surface, the distance 'r' in the universal gravitational potential energy equation decreases. Since potential energy is inversely proportional to 'r', the potential energy increases as the object gets closer to the Earth.

  • What is the equation for the acceleration due to gravity on the surface of the Earth?

    -The equation for the acceleration due to gravity on the surface of the Earth is derived from the universal gravitational potential energy equation at the Earth's surface (r = Earth's radius). It is given by g = G * MEarth / rEarth^2, where g is the acceleration due to gravity, G is the universal gravitational constant, MEarth is the mass of the Earth, and rEarth is the radius of the Earth.

  • Why is it crucial not to add a square to the variable 'r' in the universal gravitational potential energy equation?

    -It is crucial because the variable 'r' is not squared in the universal gravitational potential energy equation, unlike in Newton's Universal Law of Gravitation. Adding a square to 'r' would incorrectly alter the equation and lead to an erroneous calculation of potential energy.

  • How can the change in universal gravitational potential energy be positive?

    -While the value of universal gravitational potential energy is always negative, the change in potential energy can be positive. This occurs when work is done to bring two objects closer together, which increases the potential energy of the system.

Outlines
00:00
📚 Introduction to Universal Gravitational Potential Energy

This paragraph introduces the concept of universal gravitational potential energy, contrasting it with the previously learned concept of gravitational potential energy. It explains that while the equation for gravitational potential energy involves the mass of an object, the acceleration due to gravity, and a height (h), universal gravitational potential energy involves a formula with the universal gravitational constant (G), two masses (mass1 and mass2), and the distance (r) between their centers. The discussion highlights the applicability of the equation, emphasizing that it is relevant when the gravitational field is constant and can be used for any two objects, not just on the surface of a planet. The negative sign in the equation is also addressed, noting its role in ensuring that the potential energy is zero when objects are infinitely far apart, which is the defined zero point for potential energy.

05:02
🌌 Gravitational Potential Energy at Infinity and its Characteristics

This paragraph delves into the behavior of universal gravitational potential energy when an object is infinitely far away from Earth. It explains that at this point, the potential energy is zero due to the infinite distance (r) in the denominator of the equation. The shape of the potential energy curve is discussed, noting its concave downward shape. The paragraph also clarifies that no zero line needs to be set for universal gravitational potential energy since the zero point is predefined at infinity. It further explains that universal gravitational potential energy can never be positive, but the change in potential energy can be. The relationship between universal gravitational potential energy and the acceleration due to gravity on the surface of Earth is also explored, highlighting the derivation and substitution process. The paragraph concludes with three important points to remember: the significance of the negative sign, the requirement of two objects for gravitational potential energy, and the absence of squaring the variable 'r' in the universal gravitational potential energy equation.

Mindmap
Keywords
💡Gravitational Potential Energy
Gravitational potential energy is the energy an object possesses due to its position in a gravitational field. In the context of the video, it is defined as the mass of the object times the acceleration due to gravity (g) times the height (h) above a chosen reference level. The video emphasizes the importance of selecting an appropriate reference level, typically the Earth's surface, to calculate this energy. The concept is crucial for understanding the energy changes when an object is lifted or lowered in a gravitational field.
💡Universal Gravitational Potential Energy
Universal gravitational potential energy is a more general form of gravitational potential energy that applies to any two objects in a gravitational field, regardless of the field's constancy. It is represented by the equation U = -G * (m1 * m2) / r, where G is the universal gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between their centers of mass. Unlike the standard gravitational potential energy, universal gravitational potential energy has a negative value and does not require setting a reference level, as the zero point is defined at an infinite distance between the two objects.
💡Acceleration Due to Gravity (g)
Acceleration due to gravity (g) is the rate at which an object accelerates towards the Earth's surface when in free fall, ignoring air resistance. On Earth's surface, this value is approximately 9.81 meters per second squared. The video script discusses how this value is used in the calculation of both standard and universal gravitational potential energy, emphasizing its role in determining the force exerted by the Earth on objects in its vicinity.
💡Universal Law of Gravitation
The Universal Law of Gravitation, formulated by Sir Isaac Newton, describes the gravitational force between two objects. It states that every point mass attracts every other point mass by a force acting along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them. The video script contrasts this law with the concept of universal gravitational potential energy, highlighting that while related, they are not the same.
💡Negative Sign
The negative sign in the equation for universal gravitational potential energy indicates that the potential energy is always negative when the objects are within a finite distance of each other. This convention is used so that the potential energy approaches zero as the distance between the objects becomes infinite, which is considered the zero potential energy reference point. The negative sign ensures that work is positive when objects are brought closer together, which is consistent with the conservation of energy principle.
💡Distance (r)
In the context of gravitational potential energy, the distance (r) refers to the distance between the centers of mass of two objects experiencing a gravitational attraction. The video script explains that in the equation for universal gravitational potential energy, r is not squared, unlike in Newton's Universal Law of Gravitation, which is a common mistake students make. The variable r is crucial in determining the magnitude of the gravitational potential energy.
💡Earth's Radius
The Earth's radius is the distance from the center of the Earth to its surface. In the video, it is used to illustrate how the acceleration due to gravity on the Earth's surface can be derived from the universal gravitational constant and the Earth's mass and radius. The Earth's radius also appears in the formula for universal gravitational potential energy for an object on the Earth's surface, showing the relationship between the Earth's size and the gravitational potential energy of objects on its surface.
💡Zero Line
The zero line, or reference level, is a chosen point in a gravitational field where the potential energy is defined to be zero. In the context of the video, it is explained that for universal gravitational potential energy, the zero line is set at an infinite distance between two objects, which means that the potential energy is zero when objects are infinitely far apart. This convention allows for a consistent comparison of potential energies between different systems.
💡Constant Gravitational Field
A constant gravitational field is a field where the magnitude of the gravitational force is the same at every point. In the video, it is mentioned that the standard equation for gravitational potential energy is applicable when the gravitational field is constant, such as on the surface of a planet where the acceleration due to gravity is constant. This is in contrast to the universal gravitational potential energy, which can be used in varying gravitational fields.
💡Change in Gravitational Potential Energy
The change in gravitational potential energy refers to the difference in potential energy between two positions of an object in a gravitational field. While the potential energy itself is always negative, the change in potential energy can be either positive or negative, depending on the direction of the movement. For example, if an object is lifted against gravity, the change in potential energy is positive, indicating work done against the gravitational force. The video script explains that the change in universal gravitational potential energy can be positive, even though the potential energy itself is always negative.
💡Two Objects
The concept of two objects is essential in the discussion of gravitational potential energy, as potential energy exists between two objects interacting through gravity. The video script emphasizes that a single object in isolation cannot possess gravitational potential energy; it is the interaction between two masses that gives rise to this energy form. This is a critical point when considering the universal gravitational potential energy, which applies to any two objects in the universe.
Highlights

Introduction to universal gravitational potential energy.

Gravitational potential energy formula: mgh, where h is the height above the horizontal zero line.

The necessity of deciding the position of the horizontal zero line for using the gravitational potential energy equation.

Applicability of the gravitational potential energy equation when the gravitational field is constant.

The equation for universal gravitational potential energy involves the universal gravitational constant (G) and the masses of two objects divided by the distance between their centers of mass.

Clarification that universal gravitational potential energy is not the same as Newton's Universal Law of Gravitation.

Explanation of the negative sign in the universal gravitational potential energy equation through a graph representing the potential energy between two objects.

The zero line for universal gravitational potential energy is set at an infinite distance between two objects.

Universal gravitational potential energy can never be positive, but the change in potential energy can be.

Derivation of the acceleration due to gravity on the surface of Earth from the universal gravitational potential energy equation.

Similarity between the universal gravitational potential energy equation and the gravitational potential energy equation used in a constant gravitational field.

Three cautionary points: not forgetting the negative sign, the requirement of two objects for gravitational potential energy, and the absence of squaring the variable 'r' in the universal gravitational potential energy equation.

The importance of understanding the context and application of the gravitational potential energy equations in both constant and universal gravitational fields.

The practical application of these concepts in understanding the gravitational potential energy between objects and their interaction with Earth's gravitational field.

The significance of the universal gravitational potential energy concept in explaining the behavior of objects in the gravitational field on a global scale.

Transcripts

Browse More Related Video

AP Physics 1: Universal Gravitation Review

Gravitational Potential is NOT mgh!!!

Gravitation (9 of 17) Gravitational PE Far From Earth, the Negative Sign, An Explanation

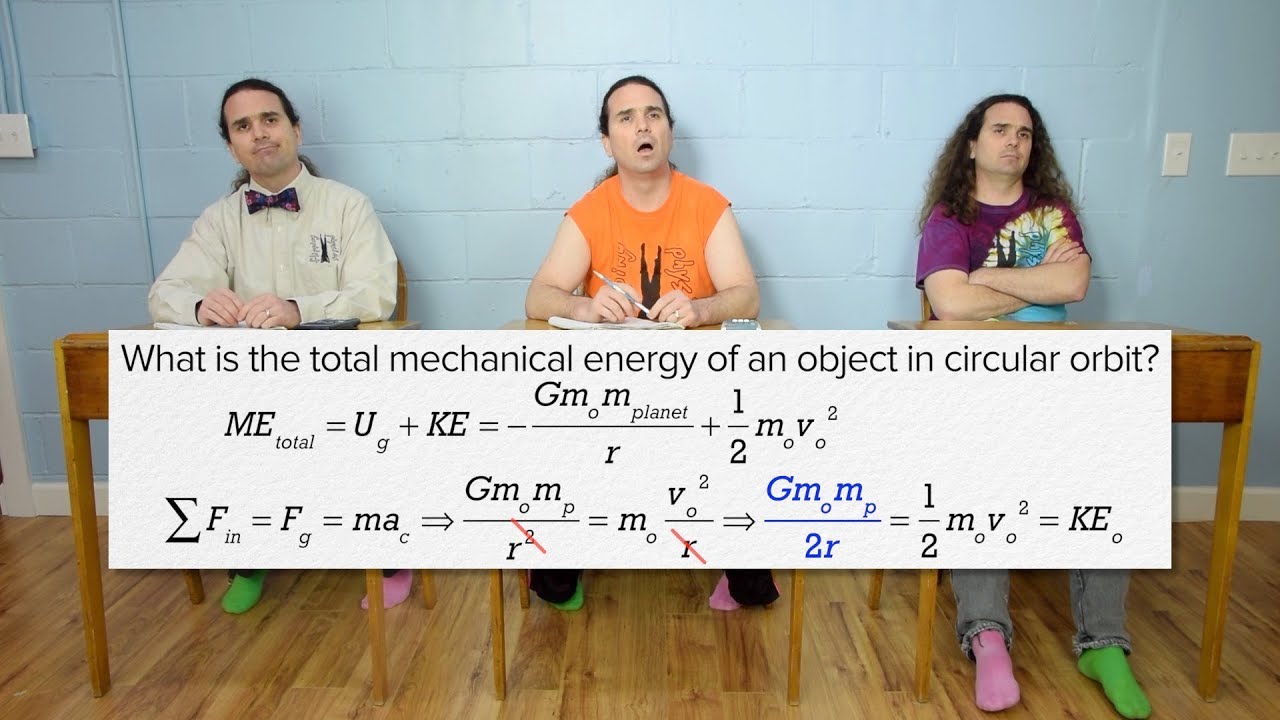
AP Physics C: Universal Gravitation Review (Mechanics) - Also for JEE/NEET

7. Kepler's Laws

13.3a Gravitational Potential Theory | A2 G-Fields | Cambridge A Level Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics EducationGravitational EnergyUniversal LawEarth-Object InteractionNegative SignificanceConstant Gravitational FieldGlobal PerspectiveEquation ComparisonBobby and BillyFlipping Physics