7. Kepler's Laws
TLDRIn this lecture, Professor Ramamurti Shankar discusses the Law of Conservation of Energy and its application to gravitational forces. He explains the concept of potential energy and how it varies with distance from a massive object, highlighting the difference between near-Earth and celestial potential energy calculations. The lecture also covers Newton's Law of Universal Gravitation and its implications for planetary motion, including the critical concept of escape velocity. The discussion emphasizes the importance of understanding fundamental physical laws and their universal applicability.
Takeaways
- 🌌 The Law of Conservation of Energy is a fundamental concept that persists even in the quantum realm, allowing us to ascribe a total energy to a system composed of kinetic and potential energies.
- 🔄 The Work-Energy Theorem is crucial in understanding how the change in kinetic energy of a body is related to the work done by it, which can be expressed as an integral of force over a path.
- 📈 In higher dimensions, the change in kinetic energy as work done is not always path-independent, leading to the concept of conservative and non-conservative forces.
- 🌐 A force is considered conservative if the work done by it is path-independent, and such forces can be derived from a potential function, leading to a conservation of energy.
- 🔄 The potential energy associated with a conservative force is the negative of the potential from which the force is derived, and this relationship holds universally for gravitational interactions.
- 🪐 Kepler's Laws describe the motion of planets around the Sun, with the first law stating that planets move in elliptical orbits with the Sun at one focus, and the second law indicating that a planet sweeps out equal areas in equal times.
- ⏳ Kepler's third law establishes a relationship between the orbital period of a planet and its semi-major axis, which is consistent across all planets in a solar system.
- 🍎 Newton's Law of Universal Gravitation states that every point mass attracts every other point mass with a force proportional to the product of their masses and inversely proportional to the square of the distance between them.
- 📊 The gravitational potential energy for a system can be defined differently based on the chosen reference point, leading to variations in the potential energy expression depending on the context (near Earth or celestial mechanics).
- 🚀 The concept of escape velocity is tied to the total energy of an object; an object with negative total energy is bound to its orbit and cannot reach infinity without gaining energy, whereas positive total energy allows for escape to infinity.
- 🌠 The existence of dark matter is inferred from the observation that the mass enclosed within the orbits of galaxies increases with distance, despite no visible matter being present, indicating the presence of unseen mass.
Q & A
What is the Law of Conservation of Energy mentioned in the lecture?
-The Law of Conservation of Energy is a powerful concept that states that the total energy in a system, which includes kinetic and potential energy, remains constant through time. This law survives even the quantum revolution and is fundamental in understanding various physical phenomena.
How does the Work-Energy Theorem relate to the change in kinetic energy of a body?
-The Work-Energy Theorem states that the change in kinetic energy of a body is equal to the work done on it by external forces. This theorem is a direct application of Newton's laws and is used to calculate the work done by a force as the integral of the force over a path.
What is the significance of the potential energy function U in the context of conservative forces?
-The potential energy function U is crucial in the context of conservative forces because it allows us to define a force whose integral (work done) is independent of the path taken. By choosing a function U and defining a force as the negative derivative of U with respect to position, we ensure that the work done by this force depends only on the initial and final positions, leading to the conservation of energy.
How can you determine if a force is conservative?
-A force is conservative if the work done by it around a closed loop is zero. This also implies that there exists a potential energy function U such that the force is the negative gradient of U. A practical test is to compare the partial derivatives of the force components with respect to each other; if they are equal, the force is conservative.
What are Kepler's three laws of planetary motion?
-Kepler's first law states that planets orbit the Sun in elliptical orbits with the Sun at one focus. The second law, also known as the law of equal areas, states that a line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. The third law establishes that the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
How does Newton's law of universal gravitation describe the force between two masses?
-Newton's law of universal gravitation states that the force between two masses is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. The force is attractive and acts along the line joining the centers of the two masses.
What is the significance of the universal gravitational constant (G)?
-The universal gravitational constant (G) is a proportionality constant in Newton's law of universal gravitation that ensures the units of force are consistent and the numerical values of the force are correct. It is a fundamental constant of nature that applies universally to all gravitational interactions.
How does the potential energy change when a body is moved in a gravitational field?
-The change in potential energy when a body is moved in a gravitational field is given by the negative of the work done by gravity. If the body is moved against the gravitational force (upward), the potential energy increases, and if the body is moved downward, the potential energy decreases.
What is the concept of escape velocity?
-The escape velocity is the minimum speed an object must have to break free from the gravitational pull of a celestial body like Earth, without further propulsion. It ensures that the object's total mechanical energy is positive, allowing it to reach infinity and not be bound by the gravitational field.
How can the energy of an orbiting celestial body be determined?
-The energy of an orbiting celestial body can be determined by considering its kinetic and potential energies. For a body in a circular orbit, the kinetic energy is exactly half the magnitude of the potential energy, and the total energy is negative. The body is bound to its orbit if the total energy is negative, can escape to infinity if the total energy is positive, and is at the borderline if the total energy is zero.
What is the implication of a negative total energy in celestial mechanics?
-A negative total energy in celestial mechanics implies that the celestial body is bound to its orbit and cannot escape to infinity. This is because at infinity, the potential energy is zero, and the kinetic energy would have to be positive, which contradicts the initial negative energy state of the body.
Outlines
📚 Recap of Previous Lecture
Professor Ramamurti Shankar begins by summarizing the previous lecture's key points, focusing on the Law of Conservation of Energy and its significance in quantum mechanics. He emphasizes the importance of understanding the relationship between kinetic and potential energy, and how this ties into the concept of work done by a force. The discussion also touches on the Work Energy Theorem and its application to various physical scenarios, including frictional forces and higher dimensions. The professor highlights the challenge of path-dependent integrals and the conditions under which the conservation of energy holds true.
🌟 Hope for Conservative Forces
The lecture continues with the exploration of conservative forces, which are integral to the conservation of energy. Professor Shankar explains how one can construct a force that ensures energy conservation by defining a potential function U and deriving the force from its negative derivatives. He asserts that every conservative force can be traced back to such a potential function, and provides a method to determine if a given force is conservative. The lecture also touches on the remarkable fact that all fundamental forces in nature are conservative, despite the complexities introduced by friction.
🪐 Historical Context of Celestial Mechanics
Professor Shankar delves into the historical context of celestial mechanics, discussing the revolutionary ideas of Copernicus and the meticulous work of Tycho Brahe and Kepler. He highlights Kepler's three laws of planetary motion, which were groundbreaking in understanding the elliptical orbits of planets and their orbital periods. The professor also reflects on the scientific process and the importance of long-term, in-depth research, contrasting the modern scientific landscape with the patience and dedication of historical figures.
📐 Understanding Elliptical Orbits
The lecture provides a detailed explanation of elliptical orbits, emphasizing the importance of understanding what an ellipse is and how it relates to planetary motion. Professor Shankar uses the concept of two thumbtacks and a string to visually describe an ellipse and its focal points. He also discusses the mathematical representation of an ellipse, differentiating between a circle and an ellipse, and how the Greeks studied these shapes. The lecture sets the stage for understanding Kepler's first law of planetary motion.
🌍 Kepler's Laws and Their Implications
Professor Shankar continues the discussion on Kepler's laws, focusing on the second law which describes the constant rate at which a planet sweeps out area in its orbit. He also addresses the third law, which relates the orbital period of a planet to its orbit size. The lecture acknowledges the existence of deviations from Kepler's laws due to factors such as gravitational interactions between planets and modifications from Einstein's theory of relativity. The professor emphasizes the significance of these laws in the broader context of celestial mechanics and the understanding of planetary motion.
🍎 Newton's Law of Universal Gravitation
The lecture introduces Newton's Law of Universal Gravitation, explaining the relationship between force, mass, and distance. Professor Shankar discusses the derivation of the gravitational force formula and the significance of the universal gravitational constant. He highlights the revolutionary aspect of this law, which posits that the same force that pulls an apple to the ground also governs the motion of celestial bodies. The lecture also touches on the importance of units and dimensional analysis in physical laws.
🌕 Applying Gravitational Law to Lunar Motion
Professor Shankar applies the Law of Universal Gravitation to the specific case of the Moon's orbit around the Earth. He uses the law to calculate the acceleration of the Moon and compares it with the acceleration of an apple falling to Earth. The lecture demonstrates how the gravitational force formula can be used to understand the motion of celestial bodies and how the acceleration of the Moon is related to the radius of its orbit and the mass of the Earth.
🌟 Kepler's Laws and Newton's Gravitational Formula
The lecture connects Kepler's laws of planetary motion with Newton's gravitational formula, showing how the latter can be used to derive the former. Professor Shankar discusses the implications of the gravitational law for planetary orbits, including the elliptical shape and the relationship between the square of the orbital period and the cube of the orbit size. He emphasizes the historical significance of Newton's work in unifying the understanding of motion on Earth and in the heavens.
🚀 Theoretical Physics and Quarks
Professor Shankar discusses the theoretical aspects of physics, using the example of quarks to illustrate the process of developing a theoretical framework and then verifying it through experimental data. He highlights the challenges of solving complex equations in physics and the importance of being able to derive and verify the consequences of a theory. The lecture touches on the historical context of scientific discovery and the process by which theories are developed and tested.
🌍 Balmer's Formula and Atomic Physics
The lecture draws a parallel between Balmer's work on spectral lines and Bohr's theory of the atom, emphasizing the importance of simplifying complex data into a manageable form to facilitate theoretical analysis. Professor Shankar explains how Balmer's formula was a precursor to Bohr's more comprehensive model, which incorporated fundamental constants like π and the electric charge. The discussion underscores the beauty of scientific theories when they successfully integrate empirical observations with mathematical formalism.
🛰️ Geosynchronous Satellites and Gravitational Formula
Professor Shankar applies the gravitational formula to the practical example of geosynchronous satellites, explaining how the formula can be used to determine the correct altitude and velocity for a satellite to maintain a constant position relative to the Earth's surface. He discusses the concept of geosynchronous orbit and the importance of the satellite's position for global communication networks. The lecture demonstrates the power of physical theories in solving real-world problems and making accurate predictions.
🌐 Global Application of Gravitational Potential
The lecture addresses the global application of gravitational potential energy, discussing the challenges of defining potential energy in different contexts. Professor Shankar clarifies the discrepancy between the potential energy formulas used near the Earth's surface and those used in celestial mechanics. He explains the freedom to add a constant to the definition of potential energy and how this reconciles the different expressions. The lecture emphasizes the importance of choosing an appropriate reference point for potential energy in different physical scenarios.
🚀 Escape Velocity and the Energy of Celestial Bodies
The lecture concludes with a discussion on escape velocity, the minimum speed required for an object to break free from a celestial body's gravitational pull. Professor Shankar explains how the escape velocity is derived from the energy considerations of an object at the surface of the Earth. He also touches on the concept of negative total energy indicating that an object is bound to orbit and cannot escape to infinity. The lecture highlights the importance of understanding energy conservation in the context of celestial mechanics and the implications for understanding the universe's structure, including the existence of dark matter.
Mindmap
Keywords
💡Conservation of Energy
💡Work-Energy Theorem
💡Potential Energy
💡Kepler's Laws
💡Newton's Laws of Motion
💡Universal Gravitation
💡Escape Velocity
💡Centrifugal Force
💡Ellipse
💡Frictional Force
Highlights
Professor Ramamurti Shankar summarizes the Law of Conservation of Energy and its importance in understanding the principles of physics.
The discussion emphasizes the significance of the Work-Energy Theorem in relating the work done by a force to the change in kinetic energy of an object.
The concept of potential energy and its dependence on the location of an object in a force field is introduced, with specific reference to gravitational and spring forces.
The integral of force over a path (work done) is explored, highlighting the conditions under which it can be expressed as a difference of two numbers, representing the potential energy at different points.
The lecture introduces the concept of conservative forces and their relationship with potential energy, stating that every conservative force is the derivative of some potential function.
A practical method to determine if a force is conservative is provided, involving the comparison of the derivatives of the force components along different axes.
The historical context of the Copernican Revolution and its impact on the understanding of the Solar System is discussed, emphasizing the role of Tycho Brahe and Kepler.
Kepler's three laws of planetary motion are presented, with an explanation of their significance in describing the orbits of planets around the Sun.
The process of deriving the gravitational force law and its application to celestial bodies is detailed, illustrating the power of Newton's insights.
The universality of the Law of Universal Gravitation is emphasized, highlighting its applicability across the universe despite being derived from Earth-based observations.
The calculation of the gravitational force between two masses is explained, including the introduction of the gravitational constant G.
The potential energy associated with gravitational force is defined and its conservation is discussed, with the total energy being the sum of kinetic and potential energy.
The concept of escape velocity is introduced, explaining the minimum velocity required for an object to break free from a gravitational pull and reach infinity.
The impact of dark matter on our understanding of the universe is briefly mentioned, illustrating the application of gravitational principles beyond visible matter.
The importance of the Law of Conservation of Energy in determining whether celestial bodies are bound to their orbits or can escape to infinity is discussed.
The role of integral calculus in verifying the law of gravitation and the need for Newton to develop it for his calculations is highlighted.
Transcripts
Browse More Related Video

5. Work-Energy Theorem and Law of Conservation of Energy

AP Physics 1: Universal Gravitation Review
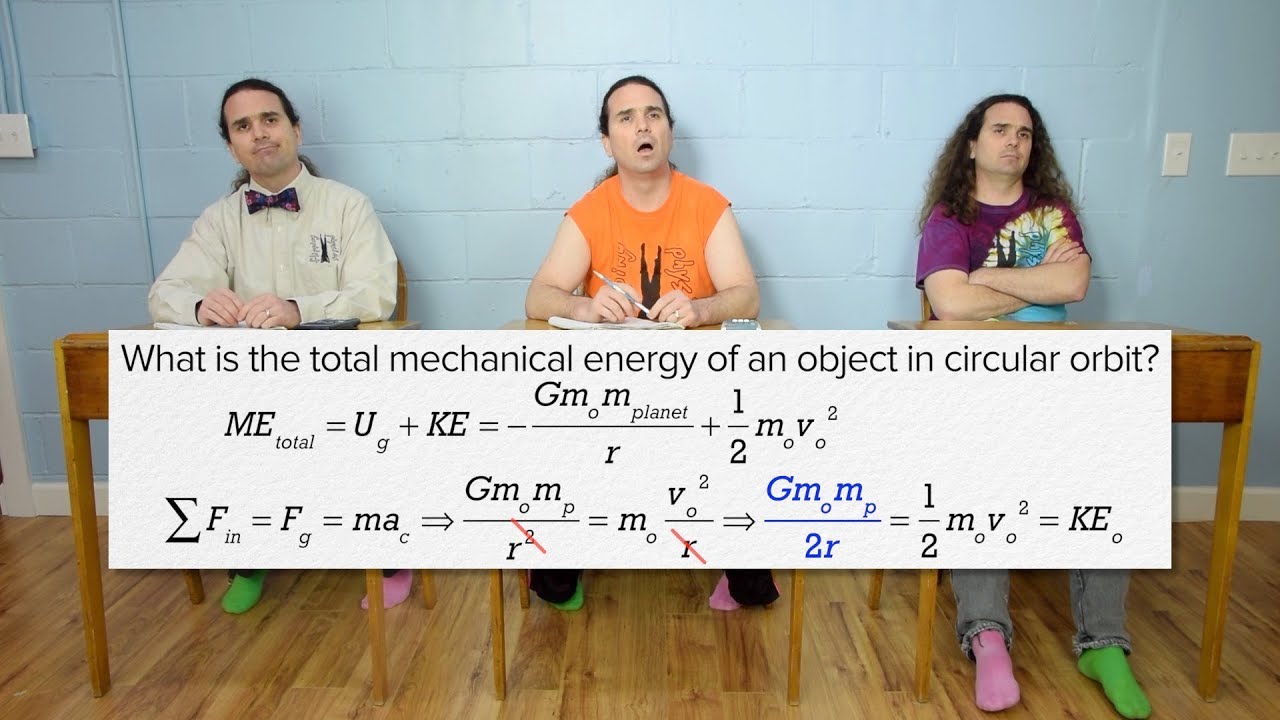
AP Physics C: Universal Gravitation Review (Mechanics) - Also for JEE/NEET

A Level Physics Revision: All of Gravitational Fields (in under 23 minutes)

Universal Gravitational Potential Energy Introduction

Gravitational Potential is NOT mgh!!!
5.0 / 5 (0 votes)
Thanks for rating: