Gravitation (9 of 17) Gravitational PE Far From Earth, the Negative Sign, An Explanation
TLDRThis video delves into the concept of gravitational potential energy, explaining the general equation involving the gravitational constant, masses of two objects, and the distance between them. It highlights the significance of the negative sign in the equation, which relates to defining zero potential energy at infinity. The video contrasts a specific equation used near Earth's surface, where potential energy is defined at the surface and increases with height, to the general equation applicable for large distances from Earth, such as in satellite orbit changes. Through examples and a potential energy graph, the video demonstrates how potential energy changes with the object's position relative to Earth, emphasizing the importance of correctly handling negative values and the consistent outcome between the two equations.
Takeaways
- 🌐 Gravitational potential energy is a measure of the energy an object possesses due to its position in a gravitational field.
- 📉 The general equation for gravitational potential energy is given by PE = -GM1M2/R, where G is the gravitational constant, M1 and M2 are the masses of the objects, and R is the distance between them.
- 🔄 The negative sign in the equation indicates that gravitational potential energy is considered zero at an infinite distance from the object and increases as objects move closer together.
- 🌍 A specific form of the equation is used near the Earth's surface, PE = mgh, where m is the mass of the object, g is the acceleration due to gravity (approximately 9.81 m/s²), and h is the height above the Earth's surface.
- 🚀 For large distances from the Earth, such as launching rockets or satellites, the general equation is preferred as the gravitational constant G varies with distance.
- 📌 The potential energy is lowest (most negative) when the object is infinitely far away from the source of gravity, as there is no gravitational attraction.
- 🔼 Increasing an object's height above the Earth's surface increases its gravitational potential energy.
- 🔽 Decreasing an object's height above the Earth's surface decreases its gravitational potential energy.
- ⚖️ The change in potential energy is calculated as the final potential energy minus the initial potential energy, with attention to the negative sign's impact on the result.
- 🔄 The concept of zero potential energy is defined differently depending on the context: at the Earth's surface for the specific equation and at infinity for the general equation.
- 📈 The relationship between distance and potential energy can be visualized on a graph, with potential energy becoming more negative (lower) as the distance decreases.
Q & A
What is the general formula for gravitational potential energy?
-The general formula for gravitational potential energy is given by PE = -G * (M1 * M2) / R, where G is the gravitational constant, M1 and M2 are the masses of the two objects, and R is the distance between them.
Why is there a negative sign in the formula for gravitational potential energy?
-The negative sign in the formula indicates that as the two objects get closer (R decreases), the potential energy becomes more negative, which means that it requires work to bring the objects closer together against the gravitational force.
What is the specific formula for gravitational potential energy near the Earth's surface?
-The specific formula for gravitational potential energy near the Earth's surface is PE = m * g * h, where m is the mass of the object, g is the acceleration due to gravity (approximately 9.81 m/s^2), and h is the height above the reference point.
How does the reference point for zero potential energy differ between the general and specific formulas?
-In the specific formula, zero potential energy is defined at the Earth's surface or the starting point of the object. In contrast, in the general formula, zero potential energy is defined at an infinite distance from the Earth, where the gravitational force is effectively zero.
What happens to the potential energy when an object is moved closer to the Earth's surface?
-When an object is moved closer to the Earth's surface, its potential energy decreases because it is moving towards the source of the gravitational force, which requires work to be done against gravity.
How does the potential energy change when an object is moved away from the Earth's surface?
-When an object is moved away from the Earth's surface, its potential energy increases. This is because work is done by gravity to move the object against the gravitational pull, storing energy in the form of potential energy.
What is the significance of the point at infinity in the context of gravitational potential energy?
-At infinity, the gravitational force and thus the potential energy between two objects is considered to be zero. This is because at an infinite distance, the objects no longer exert a gravitational force on each other.
How does the change in potential energy relate to the work done by or against gravity?
-The change in potential energy is directly related to the work done by or against gravity. Positive work done against gravity results in an increase in potential energy, while negative work (gravity doing work) results in a decrease in potential energy.
What is the relationship between the general and specific formulas for gravitational potential energy?
-The specific formula is a more straightforward version of the general formula, applicable when the object is near the Earth's surface and the acceleration due to gravity (G) can be considered constant.
How does the potential energy graph look, and what does it represent?
-The potential energy graph is a curve that shows potential energy on the y-axis and distance from the Earth on the x-axis. It typically has a negative value, becoming more negative (lower potential energy) as the distance decreases, reflecting the work done to bring an object closer to the Earth against gravitational force.
What are the key takeaways from the script regarding the calculation and understanding of gravitational potential energy?
-The key takeaways are understanding the general and specific formulas for gravitational potential energy, recognizing the significance of the negative sign, knowing how potential energy changes with the distance between objects, and being able to apply these concepts to calculate changes in potential energy in various scenarios.
Outlines
🌌 Gravitational Potential Energy Explanation
This paragraph introduces the concept of gravitational potential energy and presents the general equation for calculating it, which involves the gravitational constant (G), masses of two objects (M1 and M2), and the distance between them. The explanation focuses on the negative sign in the equation, aiming to clarify its significance and how it's used mathematically. The specific equation for calculating gravitational potential energy near the Earth's surface is also introduced, highlighting the constant value of G (acceleration due to gravity) and the height (H) through which an object is moved. The video aims to demonstrate how both general and specific equations yield the same results, despite being used in different contexts (e.g., launching a rocket or moving a satellite). The difference lies in the reference point for zero potential energy: Earth's surface for the specific equation and an infinite distance for the general one.
📈 Understanding Negative Sign and Potential Energy Changes
This paragraph delves deeper into the implications of the negative sign in the gravitational potential energy equation. It explains how the potential energy changes as an object moves away from or towards the Earth. The explanation uses a graphical representation to illustrate the relationship between distance and potential energy, emphasizing that potential energy becomes more negative (lower) as the distance decreases. The paragraph also provides a qualitative comparison of potential energy changes at different points in space, demonstrating that moving closer to Earth (decreasing distance) results in a decrease in potential energy, while moving away increases it. The importance of accurately calculating changes and being mindful of the negative sign is stressed, as it directly affects the outcome of potential energy calculations.
🚀 Summarizing Gravitational Potential Energy Concepts
In this final paragraph, the video concludes with a summary of the main points discussed regarding gravitational potential energy. It reiterates that increasing height above the Earth's surface increases potential energy, while decreasing height reduces it, regardless of the specific equation used. The key difference between the two equations is the reference point for zero potential energy: Earth's surface for the specific equation and an infinite height for the general one. The video encourages viewers to engage with the content by subscribing to the channel, liking the video, and leaving positive comments. It also prompts viewers to share the video for further educational outreach.
Mindmap
Keywords
💡Gravitational Potential Energy
💡Gravitational Constant (G)
💡Acceleration Due to Gravity
💡Negative Sign
💡Earth's Surface
💡Rocket Launch
💡Satellite Orbits
💡Work Done
💡Zero Potential Energy
💡Distance (R)
💡Change in Potential Energy
Highlights
Gravitational potential energy is a key concept in physics, explained in the video through a general equation involving the gravitational constant, masses of two objects, and the distance between them.
The general form of the gravitational potential energy equation is negative, which is discussed in the video to clarify the mathematical and physical implications of this negative sign.
A more specific equation for gravitational potential energy is provided, which is commonly used near the Earth's surface and involves the mass of an object, the acceleration due to gravity, and the height through which the object is moved.
The difference between the general and specific equations is that the zero potential energy point is defined differently; at the Earth's surface for the specific equation and at infinity for the general one.
The concept of potential energy being zero at infinity is based on the idea that an object infinitely far from the Earth experiences no gravitational attraction, hence no potential energy.
The video provides a clear example of how to use the specific equation to calculate changes in gravitational potential energy when an object is raised to a certain height.
A graphical representation of potential energy versus distance from the Earth's surface is introduced, illustrating how potential energy becomes more negative (lower) as the distance decreases.
The video explains how to calculate the change in potential energy by using the formula final potential energy minus initial potential energy, emphasizing the importance of handling negative signs correctly.
An example is given to show how the change in potential energy is quantified when moving from one point to another, both in terms of the general and specific equations.
The video emphasizes that despite the differences in the equations, the fundamental principle remains the same: moving away from the Earth's surface increases potential energy, while moving towards it decreases potential energy.
The practical applications of understanding gravitational potential energy are highlighted, such as launching rockets or satellites and changing their orbits.
The video concludes with a summary of the key points, reinforcing the understanding of the negative sign's role and the consistent results obtained from both general and specific equations.
The importance of negative signs in calculations is reiterated, as they can significantly affect the interpretation of potential energy changes.
The video encourages viewers to engage with the content by subscribing, liking, commenting, and sharing, promoting a community of learners and enthusiasts.
Transcripts
Browse More Related Video

Universal Gravitational Potential Energy Introduction

Gravitational Potential and Gravitational Potential Energy

Gravitational Potential Questions | A Level Physics | Formulas, Key Words, Graphs
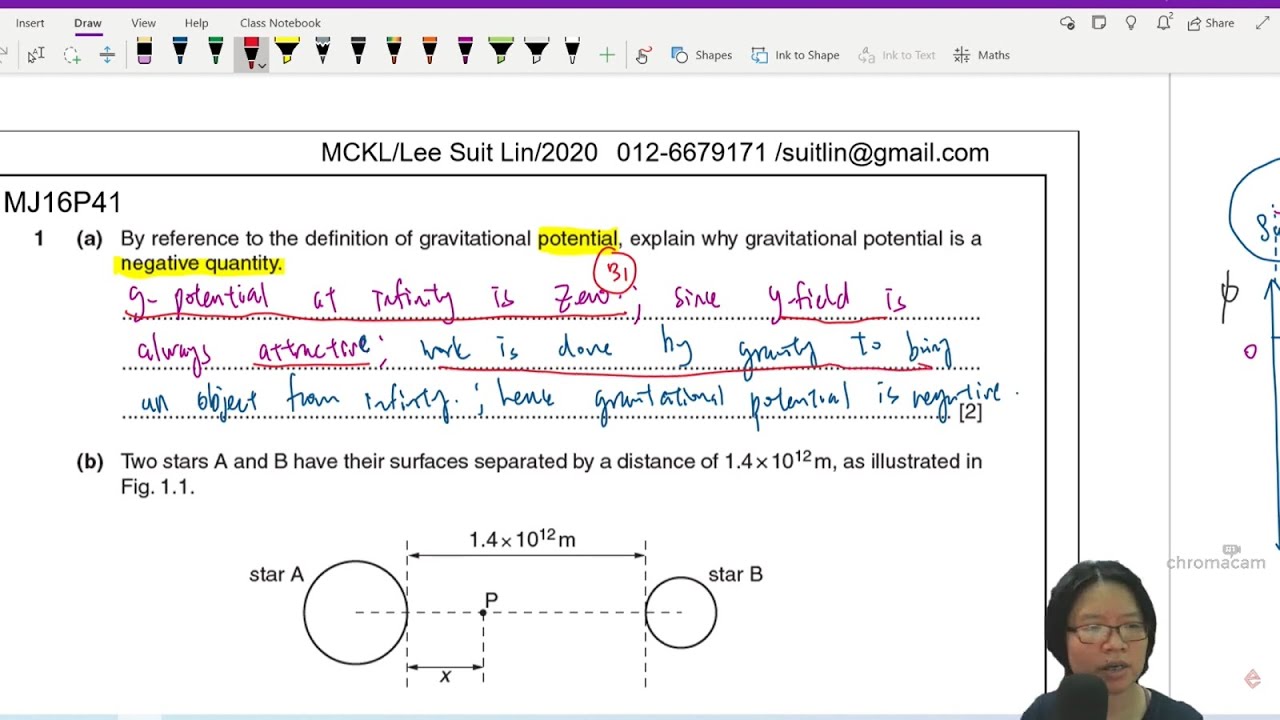
MJ16 P41 Q1 Gravitational Potential Between 2 Stars | A2 G-fields | Cambridge A Level 9702 Physics

AP Physics 1: Universal Gravitation Review

13.3a Gravitational Potential Theory | A2 G-Fields | Cambridge A Level Physics
5.0 / 5 (0 votes)
Thanks for rating: