Gravitational Potential is NOT mgh!!!

INTEGRAL PHYSICS
13 Nov 202014:57
EducationalLearning
32 Likes 10 Comments

TLDRThe video delves into the concept of gravitational potential energy, highlighting the limitations of the classical mgh formula when dealing with large distances compared to the Earth's radius. It introduces Newton's law of universal gravitation to refine the potential energy equation and explains the negative nature of gravitational potential energy. The video also touches on the implications of this understanding, such as the concept of a gravity well and its relevance to orbital mechanics and the potential energy inside and outside of Earth.

Takeaways
  • 🌋 The potential energy of a mass is related to the force of gravity acting on it and the height or displacement of the object.
  • 📉 In the past, the potential energy was simplified as mg*h, where mg is the force by gravity and h is the height.
  • 🌍 The equation mg = force by gravity is only true on the surface of the Earth and needs refinement for large distances or in space.
  • 🔧 Newton's law of universal gravitation refines the equation for force by gravity as F = G*(m1*m2)/r^2, where G is the gravitational constant, m1 and m2 are the masses, and r is the radius between them.
  • 📊 The force by gravity is negative, indicating that it acts inward towards the center of the attracting body.
  • 🔄 To find the work done by gravity, one must integrate the force by gravity over the displacement, which is a more complex calculation than the simplified mgh.
  • 🚀 The change in gravitational potential energy is equal to the work done by gravity, but with opposite signs.
  • 📉 The gravitational potential energy is given by the equation -G*M*m/R, where M is the mass of the Earth, m is the mass of the object, and R is the distance from the center of the Earth.
  • 📈 Graphing the gravitational potential energy as a function of radius shows a curve that can be approximated as linear close to the Earth's surface but must be used in its true form for large distances.
  • 🌌 No matter how high an object is lifted, it will only have a finite amount of potential energy, which approaches zero as the distance from the Earth increases.
  • 🌐 The concept of gravitational potential energy and its relationship with force by gravity has significant implications for orbital mechanics, escape velocity, and the energy of satellites in orbit.
Q & A

  • What is the concept of potential energy in the context of the script?

    -Potential energy, specifically gravitational potential energy, is the energy an object possesses due to its position in a gravitational field. In the script, it is discussed in relation to an object's height above a reference point, such as the Earth's surface, and is given by the formula PE = mgh, where m is the mass of the object, g is the acceleration due to gravity, and h is the height.

  • Why is the formula mg*h not always applicable for calculating gravitational potential energy?

    -The formula mg*h is only accurate on the surface of the Earth or for small distances where the effect of the Earth's curvature is negligible. For large distances or in space, the force of gravity cannot be assumed to be constant and must be calculated using Newton's law of universal gravitation, which takes into account the varying distance between two masses.

  • What is Newton's law of universal gravitation mentioned in the script?

    -Newton's law of universal gravitation states that the force of gravity (F) between two masses (m1 and m2) is directly proportional to the product of their masses and inversely proportional to the square of the distance (r) between their centers. The formula is F = G * (m1*m2) / r^2, where G is the gravitational constant.

  • How does the script illustrate the relationship between gravitational force and potential energy?

    -The script explains that the work done by gravity is equal to the change in gravitational potential energy, but with opposite signs. When an object falls, it loses potential energy, and this loss is equal to the work done by gravity. Conversely, when an object is raised against gravity, work is done against the gravitational force, increasing its potential energy.

  • What is the integral calculus approach used in the script to refine the potential energy calculation?

    -The script uses integral calculus to sum up an infinite number of infinitesimally small works done by gravity as an object moves from an initial radius to a final radius. This approach integrates the changing force of gravity over the distance traveled, leading to a more accurate potential energy calculation for large distances or in space.

  • How does the script explain the concept of a gravity well?

    -A gravity well is a graphical representation of gravitational potential energy as a function of distance from the center of a massive object, like the Earth. The script explains that all objects in the universe have negative potential energy relative to other objects, and we are 'trapped' in the Earth's gravity well, which is why we have negative potential energy on the Earth's surface.

  • What is the significance of the negative values in the gravitational potential energy equation?

    -The negative values indicate that the potential energy is lower than the reference point, which is typically chosen as the potential energy at infinity. In the context of the Earth, negative potential energy means that it would require work to move an object from the Earth's surface to an infinite distance away from the Earth.

  • How does the script relate the concept of potential energy to the force of gravity?

    -The script establishes that the slope of the potential energy curve at any point is equal to the force of gravity at that point. This relationship is fundamental in understanding how the potential energy changes with position and how the force of gravity influences that change.

  • What are some real-world applications of the concepts discussed in the script?

    -The concepts discussed in the script are fundamental to understanding orbital mechanics, escape velocity, satellite motion, and the behavior of objects in gravitational fields. They are also important in calculating the energy required for space travel and in predicting the motion of celestial bodies.

  • How does the script address the concept of finite potential energy?

    -The script explains that no matter how high an object is lifted, it will only ever have a finite amount of potential energy. Even if an object is lifted to an infinite distance from the Earth, the potential energy only approaches zero, which has profound implications for our understanding of the universe and gravitational fields.

  • What happens to the potential energy inside the Earth according to the script?

    -While the script does not provide a detailed explanation, it mentions that there is a whole other video dedicated to this topic. It suggests that the potential energy inside the Earth changes character and looks different from the potential energy curve outside the Earth, which will be explored in future content.

Outlines
00:00
🌋 Gravitational Potential Energy and Newton's Law of Universal Gravitation

This paragraph introduces the concept of gravitational potential energy and its relation to the force of gravity. It explains the traditional approach of calculating potential energy (mg*h) and how it applies on the surface of the Earth. The speaker then discusses the limitations of this model, especially when dealing with large distances relative to the Earth's radius. To address this, the paragraph delves into Newton's law of universal gravitation, highlighting the force of gravity as a function of the masses involved and the distance between them. The importance of considering the negative nature of the gravitational force is emphasized, and the need to refine the potential energy equation for non-surface scenarios is discussed.

05:03
📈 Calculating Work Done by Gravity and Potential Energy

The second paragraph focuses on the calculation of work done by gravity and its relationship with gravitational potential energy. It describes the process of calculating the work done by allowing an object to move through an infinitely small distance (dr) under the influence of gravity. The concept of integrating this work over an initial and final radius to find the total work done is introduced. The speaker then connects the work done by gravity to the loss of potential energy, highlighting that the change in gravitational potential energy is equal to the work done by gravity, but with opposite signs. The conclusion that the gravitational potential energy is given by an integral of the force of gravity with respect to radius is presented, setting the stage for further exploration of these concepts.

10:03
🌌 Implications of Gravitational Potential Energy and the Gravitational Well

This paragraph discusses the implications of the newly derived gravitational potential energy formula. It explains that the potential energy is always negative relative to an infinite distance from the Earth, and that living on the Earth's surface means being in a state of negative potential energy, often referred to as being trapped in a gravity well. The concept is extended to discuss the finite potential energy an object can have, no matter how high it is lifted. The paragraph also touches on the asymptotic behavior of the potential energy curve and its relation to the Earth's mass distribution. The potential energy's derivative relation to the force of gravity is highlighted, leading to discussions on escape velocity, satellite energy, and orbital mechanics. The potential energy inside the Earth is also briefly mentioned, with a promise to explore this topic in more detail in future content.

Mindmap
Keywords
💡Potential Energy
Potential energy, specifically gravitational potential energy, is the energy an object possesses due to its position in a gravitational field. In the video, it is discussed in relation to an object falling a great distance relative to the Earth's radius, emphasizing that the traditional mgh formula is not always applicable. The concept is crucial for understanding the work done by gravity and the energy changes as an object moves within a gravitational field.
💡Gravity
Gravity is the force by which a body is attracted towards the center of mass of an object, such as the Earth. In the video, the concept of gravity is explored through Newton's law of universal gravitation, which states that the force between two masses is proportional to the product of their masses and inversely proportional to the square of the distance between their centers. Gravity is central to the discussion of potential energy and the work done as an object falls or moves within a gravitational field.
💡Work Done
The work done by a force, in the context of the video, refers to the energy transferred when a force causes an object to move along a displacement. Specifically, the work done by gravity is the change in gravitational potential energy as an object falls or moves within a gravitational field. The video emphasizes that this work is the integral of the force by gravity over the displacement, which is a more accurate representation for large distances compared to the traditional mgh approximation.
💡Newton's Law of Universal Gravitation
Newton's law of universal gravitation states that every point mass attracts every other point mass by a force acting along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them. This law is fundamental to understanding the variation in gravitational force with distance, as discussed in the video, and is used to refine the equation for potential energy when dealing with large distances from a massive body like Earth.
💡Displacement
Displacement in the context of the video refers to the change in position of an object. It is a vector quantity that describes the straight-line distance from the initial position to the final position, regardless of the path taken. Displacement is integral to the calculation of work done by a force, as work is the product of the force applied and the displacement in the direction of the force.
💡Integral
An integral in mathematics represents the accumulation of a quantity, often used to calculate areas under curves or to find antiderivatives. In the video, the integral is used to find the total work done by gravity when an object moves from one radius to another in a gravitational field. By integrating the force of gravity with respect to the radius, the video provides a method to calculate the change in gravitational potential energy for large distances.
💡Radius Vector
The radius vector is a vector that points from the center of a sphere to a point on its surface. In the context of the video, the radius vector represents the distance from the center of the Earth to the object experiencing gravity. The direction of the radius vector is considered positive when it points outward from the center of the Earth, and this concept is crucial for understanding the force of gravity as a function of the radius vector.
💡Escape Velocity
Escape velocity is the minimum speed an object must reach to break free from the gravitational pull of a celestial body, like Earth, without further propulsion. It is a concept that arises from the understanding of gravitational potential energy and the work done by gravity. In the video, while not explicitly defined, the concept is implied as part of the broader discussion on the implications of gravitational potential energy and the force of gravity.
💡Orbital Mechanics
Orbital mechanics is the application of Newtonian mechanics to the motion of objects in the presence of forces, particularly gravitational forces, that cause celestial bodies to orbit. The video touches on the implications of gravitational potential energy and the force of gravity for understanding the energy of satellites in orbit and other aspects of orbital mechanics.
💡Gravitational Well
A gravitational well is a region of space where the gravitational potential energy is negative due to the presence of a massive object like Earth. The concept is used to describe the 'trapped' nature of objects within this well, as they possess negative potential energy relative to the object creating the well. In the video, the idea of a gravitational well is introduced to explain that all points in space around Earth have negative potential energy, and thus are in a sense 'trapped' by Earth's gravity.
💡Derivative
In calculus, a derivative represents the rate of change of a function with respect to its independent variable. In the context of the video, taking the derivative of the gravitational potential energy with respect to the radius vector yields the force of gravity at any point. This relationship between potential energy and force is crucial for understanding the dynamics of objects moving under the influence of gravity.
Highlights

The potential energy of a mass is typically calculated as the force of gravity acting on the mass multiplied by the height or displacement of the object (mg*h).

When a mass falls a significant distance compared to the radius of the Earth, the traditional formula for potential energy (mg*h) is no longer accurate and must be refined.

Newton's law of universal gravitation provides a more accurate model for calculating the force of gravity between two masses, taking into account the radius between them.

The force of gravity is negative, indicating that it acts inward towards the center of the attracting mass, and this is important when calculating potential energy.

To calculate the work done by gravity over a distance, one must consider the changing force of gravity as a function of radius, not just a constant value (mg).

The total work done by gravity is the infinite sum of all the tiny amounts of work done over an infinitely small change in radius (dr).

The change in gravitational potential energy is equal to the work done by gravity, with the two having opposite signs (positive work corresponds to negative potential change).

Gravitational potential energy is given by the equation -G*(M*m)/(r), where G is the gravitational constant, M and m are the masses, and r is the radius.

The graph of gravitational potential energy as a function of radius is similar to the force by gravity graph, but with a different power of r (1/r instead of 1/r^2).

Gravitational potential energy is always negative relative to an infinite distance from the attracting mass, and it can never be zero or positive.

At the surface of the Earth, objects have negative gravitational potential energy, and we are all effectively trapped in a gravity well.

The potential energy approaches zero as an object is lifted infinitely far from the Earth, but it never actually reaches zero due to the nature of the 1/r potential function.

The slope of the potential energy curve at any point is equal to the force of gravity at that point, which means that taking the derivative of potential gives us the force.

Understanding the relationship between potential energy and force is crucial for concepts such as escape velocity and orbital mechanics.

The implications of the potential energy function and its relationship to the force of gravity will be explored further in future discussions about satellites, orbits, and falling objects.

The concept of potential energy and its changes will be further examined in scenarios such as dropping an object into a hole towards the center of the Earth.

The discussion of gravitational potential energy and its calculation forms the basis for understanding a wide range of physical phenomena related to gravity.

Transcripts

Browse More Related Video

Gravitational potential energy at large distances | AP Physics 1 | Khan Academy

AP Physics 1: Universal Gravitation Review

Universal Gravitational Potential Energy Introduction

AP Physics C: Universal Gravitation Review (Mechanics) - Also for JEE/NEET

Work Done By Gravity and Gravitational Potential Energy - Physics

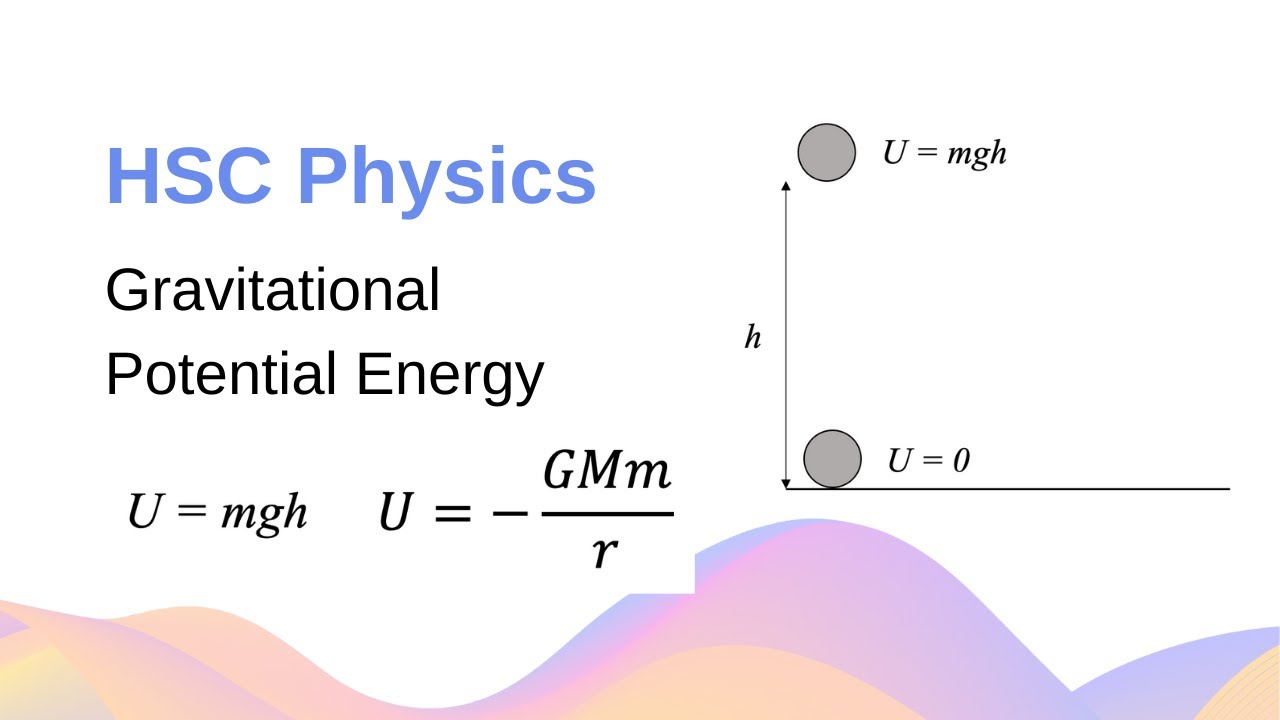
Gravitational Potential Energy & Work Done + Calculation Example // HSC Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
GravitationalPotentialPhysicsConceptsNewtonsLawSpaceOrbitEnergyWorkIntegralCalculusForceGravityPotentialEnergyGraphOrbitalMechanicsEscapeVelocity