AP Physics 1: Universal Gravitation Review

Flipping Physics
3 Apr 201508:56
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, Mr. P and his students delve into the intricacies of universal gravitation, a key topic for the AP Physics 1 exam. They explore Newton's Universal Law of Gravitation, emphasizing the formula involving the gravitational constant (big G), masses of two objects, and the square of the distance between their centers of mass. The video clarifies the difference between planet-specific gravity equations and Newton's universal law, illustrating how to calculate Earth's gravity and a satellite's linear velocity. It also addresses gravitational potential energy, contrasting the constant field equation with the universal formula, highlighting the significance of setting zero potential energy at infinite separation. The lesson concludes with a discussion on the non-existence of single-object universal gravitational potential energy, wrapping up a comprehensive review of the concept.

Takeaways
  • πŸ“š The video script is a review of universal gravitation topics for the AP Physics 1 exam.
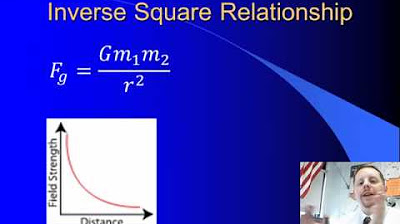
  • 🌌 Newton's Universal Law of Gravitation, also known as the big G equation, states that the force of gravity between two objects is proportional to the product of their masses and inversely proportional to the square of the distance between their centers of mass.
  • πŸ”’ The universal gravitational constant, big G, is given as 6.67 times ten to the negative 11 newtons times meters squared divided by kilograms squared.
  • πŸ“ The variable 'r' in the equation represents the distance between the centers of mass of two objects, not the radius, which can sometimes be confusing.
  • 🌍 The force of gravity equation can be planet-specific, requiring knowledge of the planet's surface gravity (little g), or universal, applicable to any celestial object.
  • 🌐 By equating the two force of gravity equations, one can solve for the acceleration due to gravity on any celestial object, including Earth.
  • πŸš€ To calculate the linear (tangential) velocity of a satellite in orbit, the centripetal force provided by gravity is equated to the mass of the satellite times its centripetal acceleration, leading to the formula for tangential velocity.
  • πŸ“‰ Gravitational potential energy in a constant field is calculated using mass, gravity, and height, but in a non-constant field, the universal gravitational potential energy formula is used, which involves big G, the masses of two objects, and the distance between their centers of mass.
  • β›” The universal gravitational potential energy is always less than or equal to zero, with zero being the potential energy when the objects are infinitely far apart.
  • πŸ’‘ The negative sign in the universal gravitational potential energy equation indicates that energy must be invested to separate two objects against gravity, making it negative when they are close.
  • 🌟 Universal gravitational potential energy is defined between two objects and cannot be attributed to a single object.
Q & A

  • What is Newton's Universal Law of Gravitation also known as?

    -Newton's Universal Law of Gravitation is also referred to as the big G equation.

  • What is the universal gravitational constant, denoted as big G?

    -The universal gravitational constant, denoted as big G, is 6.67 times ten to the negative 11 newtons times meters squared divided by kilograms squared.

  • What is the correct definition of 'r' in the context of Newton's Universal Law of Gravitation?

    -In Newton's Universal Law of Gravitation, 'r' represents the distance between the centers of mass of the two objects, not the radius.

  • How can the acceleration due to gravity (little g) on Earth be determined using the Universal Law of Gravitation?

    -By setting the magnitudes of the two equations for the force of gravity equal to one another, one can solve for the acceleration due to gravity on Earth.

  • What is the formula for linear velocity of a satellite in orbit around Earth?

    -The linear velocity (tangential velocity) of a satellite in orbit can be calculated using the formula: v = √(G * M_e / r), where M_e is the mass of the Earth, and r is the radius of the Earth plus the altitude of the satellite.

  • Why is the gravitational field considered constant on a local level?

    -On a local level, the gravitational field can be considered constant because the height is very small compared to the radius of the Earth.

  • What is the difference between the gravitational potential energy in a constant field and the universal gravitational potential energy?

    -The gravitational potential energy in a constant field is mass times the acceleration due to gravity times the vertical height above the zero line, whereas universal gravitational potential energy is the negative of big G times the mass of one object times the mass of the second object divided by r, and does not require setting a horizontal zero line.

  • Why is universal gravitational potential energy always less than or equal to zero?

    -Universal gravitational potential energy is always less than or equal to zero because it is defined with respect to the two objects being infinitely far apart, where the potential energy is zero. Any finite distance r is less than infinity, making the potential energy negative.

  • Why can't a single object have universal gravitational potential energy?

    -A single object cannot have universal gravitational potential energy because it is defined as the potential energy that exists between two objects, mass one and mass two.

  • What is the significance of the negative sign in the equation for universal gravitational potential energy?

    -The negative sign in the equation for universal gravitational potential energy indicates that the potential energy is always less than or equal to zero, reflecting the fact that it is defined relative to the objects being infinitely far apart.

  • What is the next topic that Mr. P will be reviewing after universal gravitation in his AP Physics one course?

    -The next topic that Mr. P will be reviewing is simple harmonic motion.

  • Where can students find all of Mr. P's AP Physics one review lessons organized with lecture notes?

    -Students can find all of Mr. P's AP Physics one review lessons organized with lecture notes on his website, flippingphysics.com.

Outlines
00:00
πŸš€ Newton's Universal Law of Gravitation

In the first paragraph, Mr. P introduces the concept of universal gravitation, focusing on Newton's Universal Law of Gravitation, often referred to as the 'big G equation.' He explains that the force of gravity between any two objects is proportional to the product of their masses and inversely proportional to the square of the distance between their centers of mass (r squared). Mr. P clarifies that 'big G' is the gravitational constant, approximately 6.67 x 10^-11 N(m^2/kg^2), and emphasizes the importance of understanding that 'r' represents the distance between the centers of mass, not the radius. The paragraph also distinguishes between the planet-specific equation for gravitational force and Newton's universal law, which is applicable in all circumstances. It concludes with a discussion on how to calculate the acceleration due to gravity on Earth and the concept of the gravitational field, including its representation as a vector field and how it varies with altitude and distance from Earth.

05:03
🌌 Gravitational Potential Energy and Satellite Orbits

The second paragraph delves into gravitational potential energy, contrasting it with the universal gravitational potential energy equation, which applies in non-constant gravitational fields. Mr. P points out that the universal gravitational potential energy is always less than or equal to zero, as it is defined with respect to the two objects being infinitely far apart, where the potential energy is zero. He corrects a common misconception about squaring the 'r' value in this equation, emphasizing that it should not be squared. The paragraph also addresses the concept that a single object cannot have universal gravitational potential energy, as it is a measure between two objects. Additionally, Mr. P discusses how to calculate the linear velocity of a satellite in orbit around Earth by using a free body diagram and the centripetal force equation, leading to the formula for tangential velocity based on the satellite's distance from the Earth's center.

Mindmap
Keywords
πŸ’‘Universal Gravitation
Universal Gravitation refers to the force of attraction between all masses in the universe, which is a fundamental concept in physics. In the video, it is the central theme as the script discusses Newton's Universal Law of Gravitation, also known as the 'big G equation', which quantifies this force. The script explains that the force of gravity between any two objects is proportional to the product of their masses and inversely proportional to the square of the distance between their centers of mass.
πŸ’‘Newton's Universal Law of Gravitation
Newton's Universal Law of Gravitation is a law that describes the gravitational attraction between two bodies. Defined in the script as the 'big G equation', it states that the force of gravity is equal to the gravitational constant (big G) multiplied by the product of the masses of the two objects and inversely proportional to the square of the distance between their centers of mass. This law is essential for understanding how gravity works on a universal scale and is a key point in the video's educational content.
πŸ’‘Gravitational Constant (big G)
The gravitational constant, often denoted as 'big G', is a fundamental physical constant that appears in the equations for Newton's Universal Law of Gravitation. In the script, it is given as 6.67 times ten to the negative 11 newtons times meters squared divided by kilograms squared. This constant is crucial for calculating the gravitational force between two objects and is a specific detail provided in the video to help students understand the formula for gravitational force.
πŸ’‘Mass
In the context of the video, mass refers to the amount of matter in an object, typically measured in kilograms. It is a key factor in both Newton's Universal Law of Gravitation and the calculation of gravitational force, as the force is directly proportional to the product of the masses of the two objects involved. The script emphasizes the importance of mass in understanding gravitational interactions, such as the force between the Earth and an object.
πŸ’‘Distance (r)
In the script, 'r' represents the distance between the centers of mass of two objects, which is a critical component in calculating the gravitational force using Newton's Universal Law of Gravitation. The script clarifies that 'r' is not always the radius but the actual distance between the centers of mass, which can sometimes be confusing for students. This distance is crucial in determining the strength of the gravitational force, as it is inversely proportional to the square of 'r'.
πŸ’‘Acceleration Due to Gravity (little g)
Acceleration due to gravity, often referred to as 'little g', is the rate at which an object in free fall accelerates due to the gravitational pull of a planet. In the script, it is mentioned in the context of the planet-specific equation for the force of gravity, where 'little g' is needed to calculate the force on the surface of a planet. The script also explains how to derive 'little g' using the universal gravitation equation, specifically for Earth.
πŸ’‘Centripetal Acceleration
Centripetal acceleration is the acceleration experienced by an object moving in a circular path, directed towards the center of the circle. In the video script, Bo explains how to calculate the linear velocity of a satellite in orbit using the concept of centripetal acceleration. The script illustrates that the centripetal acceleration is equal to the square of the tangential velocity divided by the radius of the orbit, which is used to derive the satellite's velocity.
πŸ’‘Gravitational Field
The gravitational field is a region around a mass where another mass would experience a gravitational force. In the script, it is described using a vector field with arrows representing the field's strength. The script explains that the gravitational field can be considered constant on a local level, such as near the Earth's surface, but it is not constant globally, leading to non-parallel field lines and varying field strengths.
πŸ’‘Gravitational Potential Energy
Gravitational potential energy is the energy an object possesses due to its position in a gravitational field. The script distinguishes between the regular gravitational potential energy, which requires a constant gravitational field, and the universal gravitational potential energy, which applies to non-constant fields. The script also emphasizes that universal gravitational potential energy is always less than or equal to zero, as it is defined relative to the energy state when objects are infinitely far apart.
πŸ’‘Satellite Orbit
A satellite orbit refers to the path a satellite takes as it revolves around a celestial body, such as Earth. In the script, the discussion of a satellite in orbit is used to illustrate how to calculate the satellite's linear velocity using the principles of centripetal acceleration and Newton's Universal Law of Gravitation. The script provides a practical application of the concepts discussed, showing how they apply to real-world scenarios like satellite motion.
Highlights

Introduction to the review of universal gravitation topics for AP Physics One exam.

Explanation of Newton's Universal Law of Gravitation, also known as the big G equation.

Definition of the universal gravitational constant, big G, as 6.67 x 10^-11 N(m^2/kg^2).

Clarification that r represents the distance between the centers of mass of two objects, not the radius.

Differentiation between the planet-specific equation for gravity and Newton's universal law.

Method to solve for the acceleration due to gravity on any celestial object using the two gravity equations.

Calculation of Earth's acceleration due to gravity by setting the two gravity equations equal to each other.

Description of the gravitational field as a vector field and its variation with altitude.

Analysis of a satellite in orbit and how to calculate its linear velocity using gravitational force.

Derivation of the formula for tangential velocity of a satellite in orbit around Earth.

Introduction to gravitational potential energy and its equation in a constant gravitational field.

Explanation of the universal gravitational potential energy equation and its distinction from the law of gravitation.

Emphasis on not squaring the r value in the universal gravitational potential energy equation.

Discussion on why universal gravitational potential energy is always less than or equal to zero.

Explanation that universal gravitational potential energy is defined between two objects and cannot exist for a single object.

Differentiation between universal gravitational potential energy and the equation involving only one mass.

Conclusion of the review lesson and invitation to the next lesson on simple harmonic motion.

Resource sharing: Website flippingphysics.com for organized AP Physics One review lessons and lecture notes.

Transcripts

Browse More Related Video

Universal Gravitational Potential Energy Introduction

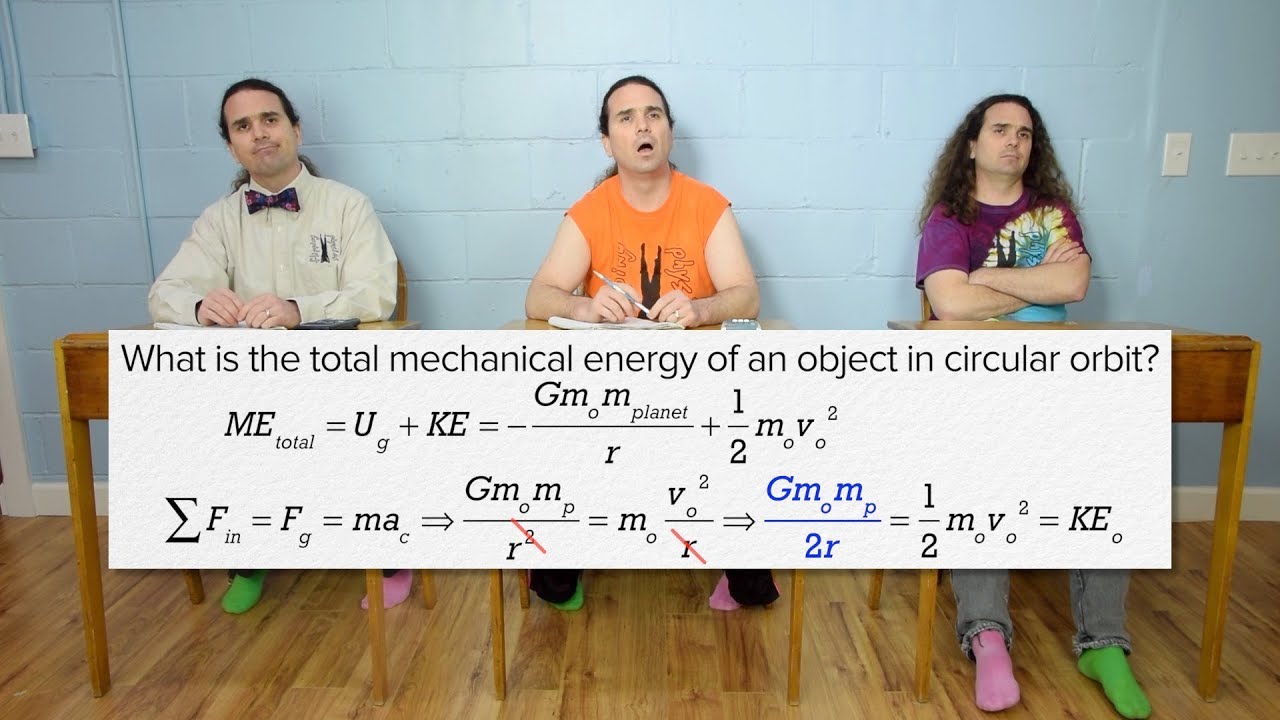
AP Physics C: Universal Gravitation Review (Mechanics) - Also for JEE/NEET

A Level Physics Revision: All of Gravitational Fields (in under 23 minutes)

7. Kepler's Laws

High School Physics - Newton's Law of Universal Gravitation

Gravitational Potential is NOT mgh!!!

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Universal GravitationAP PhysicsNewton's LawGravity EquationCelestial ObjectsSatellite OrbitCentripetal ForceGravitational FieldPotential EnergyEducational Content