AP Physics C: Universal Gravitation Review (Mechanics) - Also for JEE/NEET
TLDRThis video script offers a comprehensive review of universal gravitation for AP Physics C students. It covers the fundamental concepts, including the equations for gravity's force and Newton's Universal Law of Gravitation. The script delves into gravitational potential energy, escape velocity, and the mechanical energy of objects in orbit. It also corrects a common misconception about gravitational potential energy inside a planet and discusses Kepler's laws, emphasizing the derivation of the third law, which relates the orbital period to the radius. The engaging dialogue format helps clarify complex topics, making it an informative resource for students.
Takeaways
- 📚 The script is a review of universal gravitation for the AP Physics C mechanics curriculum.
- 🔍 The equation for the force of gravity acting on an object is mass times acceleration due to gravity, with an assumed subscript 'o' for the mass of the object.
- 🌍 Newton's Universal Law of Gravitation, also known as 'The Big G Equation', describes the gravitational attraction between any two masses, with 'big G' being the Universal Gravitational Constant.
- 📏 The distance 'r' in the gravitational equations is the distance between the centers of mass of two objects, not necessarily the radius.
- ⚖️ The force of gravity can be equated between the two equations, leading to the formula for acceleration due to gravity on Earth involving 'big G', Earth's mass, and Earth's radius.
- 🪢 The concept of gravitational potential energy is discussed, with a constant gravitational field approximation leading to a simple formula involving mass, gravity, and height.
- 📉 The gravitational potential energy inside a planet is not linear and requires a different approach, with an acknowledgment of a previous teaching error.
- 🚀 The minimum work necessary to remove an object from a planet, known as binding energy, is derived using principles of energy conservation.
- 🌌 The escape velocity, which is the minimum velocity needed to launch an object off Earth without it returning, is calculated using conservation of mechanical energy.
- 🛰️ The total mechanical energy of an object in circular orbit is derived, showing a relationship between kinetic and potential energy.
- 📐 Kepler's Laws are briefly mentioned, with an emphasis on deriving Kepler's Third Law, which relates the period of an orbiting object to its radius.
Q & A
What is the equation for the force of gravity acting on an object on Earth?
-The force of gravity acting on an object, or weight, is given by the equation F = m * g, where F is the force, m is the mass of the object, and g is the acceleration due to gravity (approximately 9.81 m/s² on Earth).
What is Newton’s Universal Law of Gravitation?
-Newton's Universal Law of Gravitation states that every point mass attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. The equation is F = G * (m1 * m2) / r², where F is the force, G is the gravitational constant (6.67 x 10⁻¹¹ N m²/kg²), m1 and m2 are the masses of the objects, and r is the distance between the centers of the two masses.
What is the significance of the gravitational constant, G?
-The gravitational constant, G, is a fundamental constant that quantifies the strength of the gravitational force between two objects. It has a value of 6.67 x 10⁻¹¹ N m²/kg².
How does the distance between two objects affect the gravitational force between them?
-The gravitational force between two objects is inversely proportional to the square of the distance between their centers. This means that as the distance (r) increases, the force decreases by the factor of r².
What is the difference between the force of gravity and gravitational potential energy?
-The force of gravity is the attractive force between two masses, while gravitational potential energy is the energy stored in an object due to its position in a gravitational field. The gravitational potential energy in a constant field is given by U = m * g * h, and in a universal context by U = -G * (m1 * m2) / r.
What is meant by 'binding energy' in the context of gravitational potential energy?
-Binding energy is the minimum amount of energy required to completely remove an object from the gravitational influence of another object, effectively taking it to an infinite distance where the gravitational potential energy becomes zero.
What is escape velocity and how is it calculated?
-Escape velocity is the minimum velocity needed for an object to escape the gravitational pull of a planet without further propulsion. It is calculated using the formula v_escape = sqrt(2 * G * M / r), where G is the gravitational constant, M is the mass of the planet, and r is the radius of the planet.
What is the total mechanical energy of an object in circular orbit?
-The total mechanical energy of an object in circular orbit is the sum of its kinetic energy and gravitational potential energy. It is given by the equation E_total = -G * (m * M) / (2 * r), where m is the mass of the orbiting object, M is the mass of the planet, and r is the radius of the orbit.
What is Kepler’s First Law of planetary motion?
-Kepler's First Law, also known as the Law of Orbits, states that all planets move in elliptical orbits with the Sun at one of the two foci of the ellipse.
What does Kepler’s Second Law state about planetary motion?
-Kepler's Second Law, or the Law of Areas, states that a line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. This implies that a planet moves faster when it is closer to the Sun and slower when it is farther from the Sun.
How is Kepler’s Third Law derived and what does it state?
-Kepler's Third Law, the Law of Periods, relates the orbital period of a planet to its orbital radius. It is derived by equating the gravitational force to the centripetal force required for circular motion. The law states that the square of the orbital period (T²) is proportional to the cube of the semi-major axis of the orbit (r³), given by the formula T² = (4π² / G * M) * r³.
Outlines
🌍 Universal Gravitation and Newton's Laws
This paragraph introduces the concept of universal gravitation, focusing on the fundamental equations describing gravitational force. It clarifies the difference between the gravitational force acting on an object near Earth's surface and Newton's Universal Law of Gravitation, which applies to any two masses in the universe. The paragraph emphasizes the importance of understanding the variables involved, such as mass, the gravitational constant (Big G), and the distance between the centers of mass (r). It also touches on the concept of gravitational potential energy, highlighting the difference between a constant gravitational field near Earth's surface and the varying gravitational field at different altitudes or distances from Earth.
🚀 Gravitational Potential Energy and Escape Velocity
The second paragraph delves into the specifics of gravitational potential energy, both in the context of a constant field and the universal formula involving any two masses. It corrects a common mistake regarding the calculation of potential energy inside a planet and introduces the concept of binding energy. The paragraph also discusses the minimum work required to remove an object from a planet entirely, known as binding energy, and introduces the concept of escape velocity, which is the minimum velocity needed for an object to break free from a planet's gravitational pull without further propulsion.
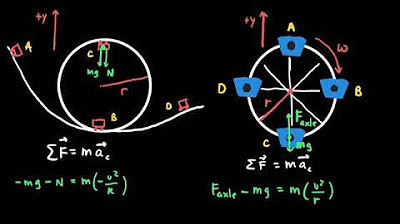
🛰️ Total Mechanical Energy and Circular Orbits
This segment explores the total mechanical energy of an object in a circular orbit, explaining the relationship between kinetic and potential energy in such a scenario. It demonstrates how the velocity of the object can be derived from the gravitational force acting as the centripetal force. The paragraph also discusses Kepler's laws of planetary motion, providing a basic understanding of the first two laws and a detailed derivation of the third law, which relates the orbital period of an object to its radius, showing that the square of the period is proportional to the cube of the radius.
📚 Summary of Universal Gravitation Review
The final paragraph wraps up the review of universal gravitation by summarizing the key points covered in the previous sections. It reiterates the importance of understanding the equations and concepts related to gravitational force, potential energy, and the mechanics of celestial bodies in orbit. The paragraph concludes by encouraging viewers to continue their learning with additional resources provided by the instructor, such as a review of simple harmonic motion or the AP Physics C review webpage.
Mindmap
Keywords
💡Universal Gravitation
💡Acceleration Due to Gravity
💡Newton’s Universal Law of Gravitation
💡Gravitational Potential Energy
💡Binding Energy
💡Escape Velocity
💡Circular Orbit
💡Kepler's Laws
💡Eccentricity
💡Centripetal Acceleration
💡Angular Velocity
Highlights
Introduction to the review of universal gravitation in the context of AP Physics C mechanics curriculum.
Explanation of the basic equation for gravitational force, emphasizing the assumed subscript 'o' for the object's mass.
Introduction to Newton's Universal Law of Gravitation, also known as 'The Big G Equation'.
Clarification of the Universal Gravitational Constant, its value, and its role in gravitational attraction.
Discussion on the importance of understanding the distance 'r' as the distance between the centers of mass of two objects.
Equivalence of the two gravity equations and the derivation of acceleration due to gravity on Earth.
Explanation of how gravity can be considered constant at a local level, with a value of 9.81 m/s².
Introduction to gravitational potential energy in a constant field and its formula.
Differentiation between gravitational potential energy in a constant field and the universal gravitational potential energy formula.
Correction of a common mistake regarding the universal gravitational potential energy formula.
Discussion on the impossibility of positive universal gravitational potential energy and the concept of a zero reference line.
Illustration of the relationship between an object's position relative to Earth and its gravitational potential energy.
Correction of a long-standing error regarding gravitational potential energy inside the planet and acknowledgment of the mistake.
Introduction to the concept of binding energy and its calculation as the minimum work to remove an object from a planet.
Explanation of escape velocity and its derivation as the minimum velocity needed for an object to leave Earth without returning.
Determination of the total mechanical energy of an object in circular orbit and its relation to gravitational potential and kinetic energy.
Introduction to Kepler's Three Laws and their significance in understanding celestial mechanics.
Derivation of Kepler's Third Law, illustrating the relationship between the orbital period and radius.
Conclusion of the universal gravitation review and invitation to further learning resources.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: