2015 AP Physics 1 free response 3c
TLDRThe video script discusses the principles of quantitative reasoning and potential energy in relation to a spring-mass system. It explores two scenarios where a block compresses a spring by varying degrees, leading to different potential and kinetic energies. The script derives expressions for the stopping distance based on the conservation of energy and the work done by friction, concluding that compressing the spring twice as much results in a fourfold increase in potential energy, kinetic energy at the point of release, and the stopping distance, which is calculated to be 12d.
Takeaways
- 📈 The potential energy stored in a compressed spring is proportional to the square of the compression (δx).
- 🔄 When the spring is released, the potential energy is converted into kinetic energy.
- 🚀 The kinetic energy at the point of release (x=0) is equal to the potential energy stored in the spring.
- 🔢 For the given scenarios, compressing the spring by 2d results in four times the potential energy compared to compressing it by d.
- 🏃 The kinetic energy at x=0 dictates the initial force exerted by the spring on the block.
- 🛑 The stopping distance is determined by the work done against friction, which is the conversion of kinetic energy into heat.
- 👎 Friction does negative work as it acts in the opposite direction of the block's motion.
- 📌 The work done by friction is calculated by multiplying the coefficient of friction (μ), mass (m), gravitational field (g), and the distance (3d).
- 📈 The stopping distance increases with the increase in kinetic energy, which is directly related to the potential energy stored in the spring.
- 🔄 The final stopping distance for the block is 12d when the spring is compressed twice as much (2d) as in the initial scenario (d).
- 📋 The expression for the new final position of the block in terms of d is 12d, derived from the analysis of potential and kinetic energy, and the work done by friction.
Q & A
What is the main focus of the video transcript?
-The main focus of the video transcript is to use quantitative reasoning, including equations, to develop an expression for the new final position of a block when a spring is compressed.
How does the potential energy of a compressed spring relate to the amount of compression?
-The potential energy of a compressed spring is proportional to the square of the amount of compression. This means that if the compression is doubled, the potential energy increases by a factor of four.
What is the relationship between potential energy and kinetic energy in the context of the spring and block?
-At the point when the block loses contact with the spring, the potential energy is converted into kinetic energy. The amount of kinetic energy is equal to the potential energy when the spring was compressed.
How does the stopping distance of the block change when the spring compression is doubled?
-When the spring compression is doubled, the stopping distance of the block increases by a factor of four. This is because the potential and kinetic energies are quadrupled, and the work done by friction (which stops the block) is proportional to these energies.
What is the formula for the potential energy of a compressed spring?
-The formula for the potential energy of a compressed spring is given by PE = (1/2) * k * (delta x)^2, where k is the spring constant and delta x is the amount of compression.
What is the work done by friction and how is it related to the kinetic energy?
-The work done by friction is equal to the change in kinetic energy, which is the difference between the initial and final kinetic energies. It is calculated as the product of the friction coefficient, the mass of the block, the gravitational field, and the stopping distance.
How can you calculate the stopping distance of the block?
-The stopping distance can be calculated by dividing the initial kinetic energy by the force of friction. This gives the distance the block travels before coming to a stop due to the work done by friction.
What is the expression for the new final position of the block when the spring is compressed twice as much?
-The new final position of the block, when the spring is compressed twice as much, is given by the expression 12d, where d is the original compression distance.
How does the kinetic energy at x equals zero relate to the potential energy in scenario one?
-The kinetic energy at x equals zero is equal to the potential energy in scenario one. This is because all the potential energy stored in the compressed spring is converted into kinetic energy when the block is released.
What is the role of the coefficient of friction in determining the stopping distance?
-The coefficient of friction plays a crucial role in determining the stopping distance as it affects the force of friction, which is directly involved in the work-energy calculation that gives the stopping distance.
What is the relationship between the kinetic energy in scenario one and scenario two?
-The kinetic energy in scenario two is four times the kinetic energy in scenario one because the potential energy, which is converted into kinetic energy, is also four times greater when the spring is compressed twice as much.
Outlines
📚 Quantitative Analysis of Spring Compression
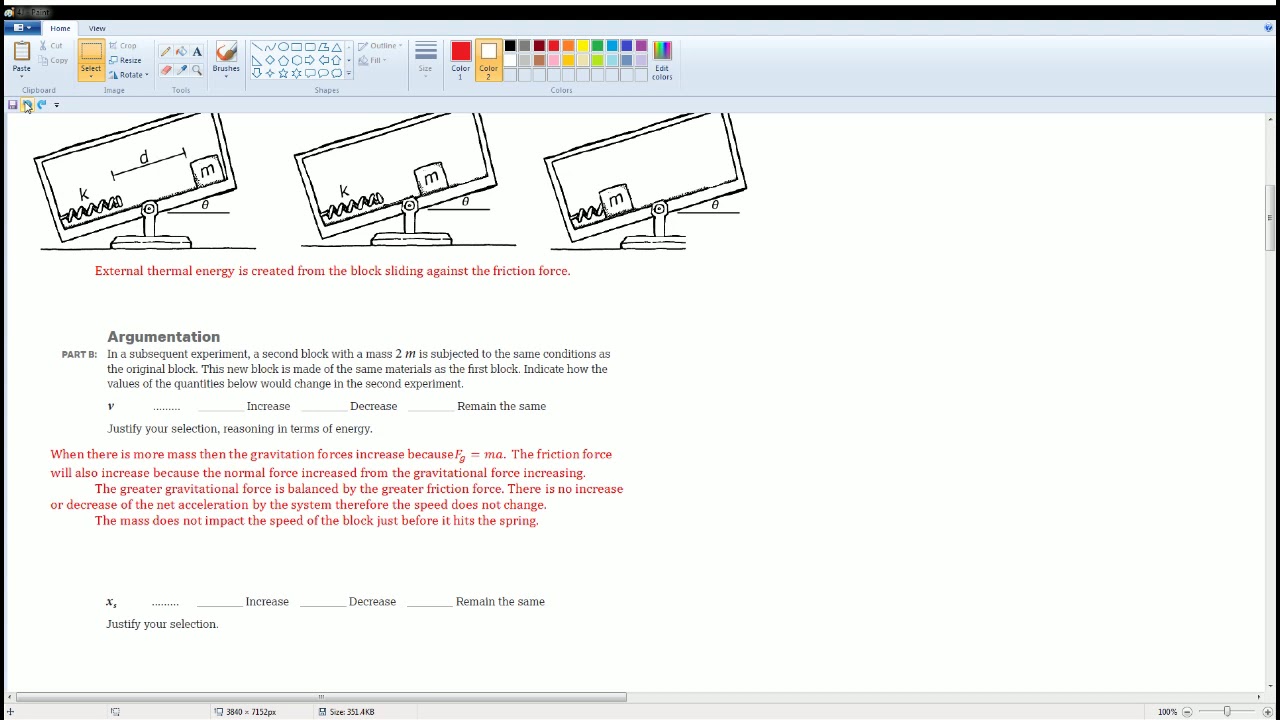
This paragraph introduces the task of using quantitative reasoning to develop an expression for the final position of a block after compressing a spring. The voiceover explains setting up a table to analyze two scenarios of spring compression, one with a compression of 'd' and another with '2d'. The focus is on understanding the potential energy stored in the spring when compressed and how it relates to the kinetic energy when the block is released. The concept is extended to calculate the stopping distance based on the work done against friction, which is found to be three times 'd' for the first scenario. The explanation emphasizes the non-linear relationship between the compression and potential energy, where compressing the spring twice as much results in four times the potential energy and consequently four times the stopping distance.
🔧 Calculating Stopping Distance with Friction in Mind
The second paragraph delves into the calculation of stopping distance when friction is considered. It builds upon the previous analysis by incorporating the work done by friction, which is negative due to the opposing force of friction to the direction of motion. The voiceover provides a formula for the kinetic energy at the point where the block loses contact with the spring and uses this to derive the stopping distance. The explanation shows that the stopping distance is directly proportional to the potential and kinetic energy, thus doubling the compression results in a quadrupling of the stopping distance. The paragraph concludes with a clear statement that instead of stopping at '3d' or '6d' as initially proposed, the block will now stop at '12d', reinforcing the concept that the stopping distance increases with the square of the spring compression.
Mindmap
Keywords
💡Quantitative Reasoning
💡Potential Energy
💡Kinetic Energy
💡Stopping Distance
💡Spring Constant
💡Coefficient of Friction
💡Work Done by Friction
💡Gravitational Field
💡Force of Friction
💡Compression
💡Energy Conversion
Highlights
Developing an expression for the final position of a block using quantitative reasoning and equations.
Setting up a table to organize the scenarios for part c.
Considering two scenarios for spring compression: compressing by d and compressing by 2d.
Exploring the potential energy when the spring is compressed in both scenarios.
Deriving that the potential energy increases with the square of the compression.
Calculating the kinetic energy when the block loses contact with the spring.
Understanding that the potential energy is converted into kinetic energy.
Discussing the relationship between kinetic energy and stopping distance.
Using the work done by friction to determine the stopping distance.
Calculating the work done by friction as a function of the coefficient of friction, mass, gravitational field, and distance.
Deriving the equation for stopping distance in terms of kinetic energy and the force of friction.
Doubling the spring compression results in four times the potential energy and kinetic energy.
The stopping distance increases proportionally to the kinetic energy.
Calculating the new stopping distance as 12d instead of the initially proposed 3d or 6d.
The mathematical approach confirms the relationship between spring compression, potential and kinetic energy, and stopping distance.
The final position of the block is expressed in terms of d, providing a clear and quantifiable result.
The process demonstrates the practical application of quantitative reasoning in physics problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: