2015 AP Physics 1 free response 3a

Khan Academy
12 Apr 201607:45
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses a physics problem involving a block and a spring. Initially at rest, the block compresses a spring by moving from position x=0 to x=-D. Once released, the block oscillates, converting potential energy into kinetic energy until reaching x=0, where the spring is uncompressed. The block's motion continues to x=3D, where it stops due to friction, converting kinetic energy into heat. The script instructs viewers to sketch graphs of the block's kinetic and potential energy versus its position, highlighting the conservation of energy principle and the effects of friction.

Takeaways
  • πŸ“Œ The block starts at position x=0 in contact with an uncompressed spring of negligible mass.
  • πŸ”™ The block is pushed from x=0 to x=-D, compressing the spring by an amount Ξ”x=D.
  • βš™οΈ The work done to compress the spring is stored as potential energy in the spring-block system.
  • πŸš€ Upon release, the potential energy is converted into kinetic energy, accelerating the block.
  • πŸ”„ At x=0, the spring is uncompressed, and the block's kinetic energy is at its peak.
  • πŸ“ˆ The potential energy curve is parabolic, increasing with the square of the spring compression.
  • 🏎️ The block's kinetic energy starts at zero and increases until it reaches x=0, where it equals the initial potential energy.
  • πŸ›‘ Friction, represented by the coefficient ΞΌ, causes the block to eventually stop at x=3D.
  • πŸ”½ Due to friction, the kinetic energy decreases linearly from x=0 to x=3D, converting into heat.
  • πŸ“Š The energy vs. position graph consists of a parabolic potential energy curve and a linear kinetic energy curve.
  • 🌐 The total energy remains constant throughout the motion, transitioning from potential to kinetic and finally to heat due to friction.
Q & A

  • What is the initial position of the block?

    -The block is initially at position x = 0, where it is in contact with the uncompressed spring.

  • What happens to the block when it is pushed back along the surface?

    -The block is pushed from position x = 0 to x = -D, compressing the spring by an amount delta x = D.

  • What type of energy is stored in the spring-block system when the spring is compressed?

    -When the spring is compressed, potential energy is stored in the spring-block system.

  • How is the potential energy of a compressed spring calculated?

    -The potential energy of a compressed spring is calculated as one-half times the spring constant (k) times the square of the compression amount (D^2).

  • What happens to the potential energy when the block is released at x = 0?

    -When the block is released, the potential energy is converted into kinetic energy, which accelerates the block until it reaches x = 0, where the spring is uncompressed.

  • What causes the block to eventually come to rest at position x = 3D?

    -The block comes to rest at x = 3D due to the constant force of friction acting on it as it moves through the rough part of the track.

  • What is the relationship between the kinetic energy of the block and its position between x = -D and x = 3D?

    -The kinetic energy of the block starts at zero when it is stationary and increases as it accelerates due to the released potential energy. It then decreases linearly as friction converts it into heat.

  • How does the friction force affect the block's energy?

    -The friction force does negative work on the block, converting kinetic energy into heat at a constant rate, causing the block to decelerate and eventually come to rest.

  • What is the role of air resistance in this problem?

    -In this problem, air resistance is assumed to be negligible, so it does not affect the block's motion or energy conversion.

  • What is the significance of the graph of potential energy versus position?

    -The graph of potential energy versus position shows the energy stored in the spring-block system as the spring is compressed and then released. It resembles the left side of a parabola, indicating the non-linear relationship between potential energy and the compression of the spring.

  • What can be inferred from the graph of kinetic energy versus position?

    -The graph of kinetic energy versus position indicates the conversion of potential energy into kinetic energy and then its decrease due to friction. It shows a linear decrease in kinetic energy as the block moves from x = 0 to x = 3D, reflecting the constant deceleration caused by friction.

Outlines
00:00
πŸ“ˆ Initial Conditions and Energy Transformation

The video begins by describing a scenario where a block is initially at rest at position x=0 with an uncompressed spring. The block is then pushed back to x=-D, compressing the spring by an amount delta x=D. This action stores potential energy in the spring-block system, which is later converted into kinetic energy when the block is released. The block moves along a frictionless surface and eventually comes to rest at position x=3D due to friction. The video emphasizes the conservation of energy, transitioning from potential to kinetic energy, and finally to heat due to friction. The potential energy of the compressed spring is given by the formula U=(1/2)k*D^2, where k is the spring constant.

05:01
πŸ”„ Conservation of Energy and Frictional Effects

This paragraph discusses the conservation of energy principle, stating that the sum of potential and kinetic energy remains constant from x=-D to x=0. The kinetic energy starts at zero and increases as the block accelerates due to the released spring. The video explains that if there were no friction or air resistance, the block would continue moving indefinitely. However, due to the presence of kinetic friction with a coefficient mu, the block eventually stops at x=3D. The kinetic energy is converted into heat, illustrating the law of conservation of energy where energy transforms from one form to another but is neither created nor destroyed. The frictional force, being constant, causes a linear decrease in kinetic energy as the block moves from x=0 to x=3D.

Mindmap
Keywords
πŸ’‘Block
The 'block' refers to the main object in the video that interacts with the spring and the track. It is initially at rest at position x=zero and is pushed back to compress the spring by an amount D. The block's movement and the resulting kinetic and potential energies are central to the video's theme of energy transformation.
πŸ’‘Spring
The 'spring' is an elastic object that can be compressed or stretched, storing potential energy when deformed. In the video, the spring is initially uncompressed and then compressed by pushing the block, which is a key element in the energy transformation process.
πŸ’‘Potential Energy
Potential energy is the stored energy an object has due to its position or condition. In the video, the potential energy is associated with the compressed spring, calculated as one-half times the spring constant times the square of the compression amount (D).
πŸ’‘Kinetic Energy
Kinetic energy is the energy of motion an object possesses. In the video, as the block moves from x=-D to x=zero, the potential energy is converted into kinetic energy, which propels the block forward.
πŸ’‘Friction
Friction is the resistive force that opposes the relative motion of objects in contact with each other. In the video, friction is the force that eventually stops the block, converting its kinetic energy into heat as it comes to rest at x=3D.
πŸ’‘Energy Conservation
Energy conservation is the principle that the total amount of energy in an isolated system remains constant, though it may change forms. The video demonstrates this principle through the transformation of potential energy to kinetic energy and then to heat due to friction.
πŸ’‘Work
Work is the measure of energy transfer that occurs when an object is moved by a force acting on it. In the video, work is done on the spring when the block is pushed to compress it, storing energy as potential energy.
πŸ’‘Acceleration
Acceleration is the rate of change of velocity of an object with time. In the video, the block experiences acceleration as the spring pushes back after being compressed, converting potential energy into kinetic energy.
πŸ’‘Deceleration
Deceleration is the decrease in the rate of motion of an object, which is the negative acceleration. In the video, the block decelerates as it moves from x=zero to x=3D due to the constant force of friction.
πŸ’‘Coefficient of Kinetic Friction
The coefficient of kinetic friction is a dimensionless scalar value that represents the ratio of the frictional force to the normal force between two bodies in contact. In the video, this coefficient, denoted by mu, determines the magnitude of the frictional force acting on the block as it moves on the rough track.
πŸ’‘Graphs
Graphs are visual representations of data or functions, showing relationships between variables. In the video, the graphs of potential energy and kinetic energy as functions of the block's position are used to illustrate the energy transformations throughout the block's motion.
Highlights

A block is initially at position x=zero in contact with an uncompressed spring of negligible mass.

The block is pushed back along a frictionless surface from x=zero to x=-D, compressing the spring by an amount delta x=D.

The block starts at x=zero and the spring is uncompressed before being pushed to the left to compress it by D.

When the block is released at x=zero, it enters a rough part of the track and comes to rest at position x=3D.

The work done to compress the spring gets stored as potential energy in the spring-block system.

The potential energy of the compressed spring is equal to one-half times the spring constant times the compression squared.

The potential energy curve is parabolic, increasing with the square of the spring compression.

The kinetic energy of the block starts at zero and increases as the spring accelerates the block until x=zero.

The sum of potential and kinetic energy remains constant from x=negative D to x=zero due to the conservation of energy principle.

At x=zero, all potential energy has been converted into kinetic energy.

The block comes to rest at x=3D due to the conversion of kinetic energy into heat caused by friction.

The frictional force is constant and causes a linear decrease in kinetic energy as the block slows down.

The energy lost to friction is an example of energy transformation, not creation or annihilation.

The graph of energy versus position is crucial for understanding the energy dynamics in the system.

The potential energy graph is the left side of a parabola, while the kinetic energy graph decreases linearly.

The problem illustrates fundamental principles of classical mechanics, including energy conservation and frictional forces.

Transcripts

Browse More Related Video

2015 #3 Free Response Question - AP Physics 1 - Exam Solution

2015 AP Physics 1 free response 3c

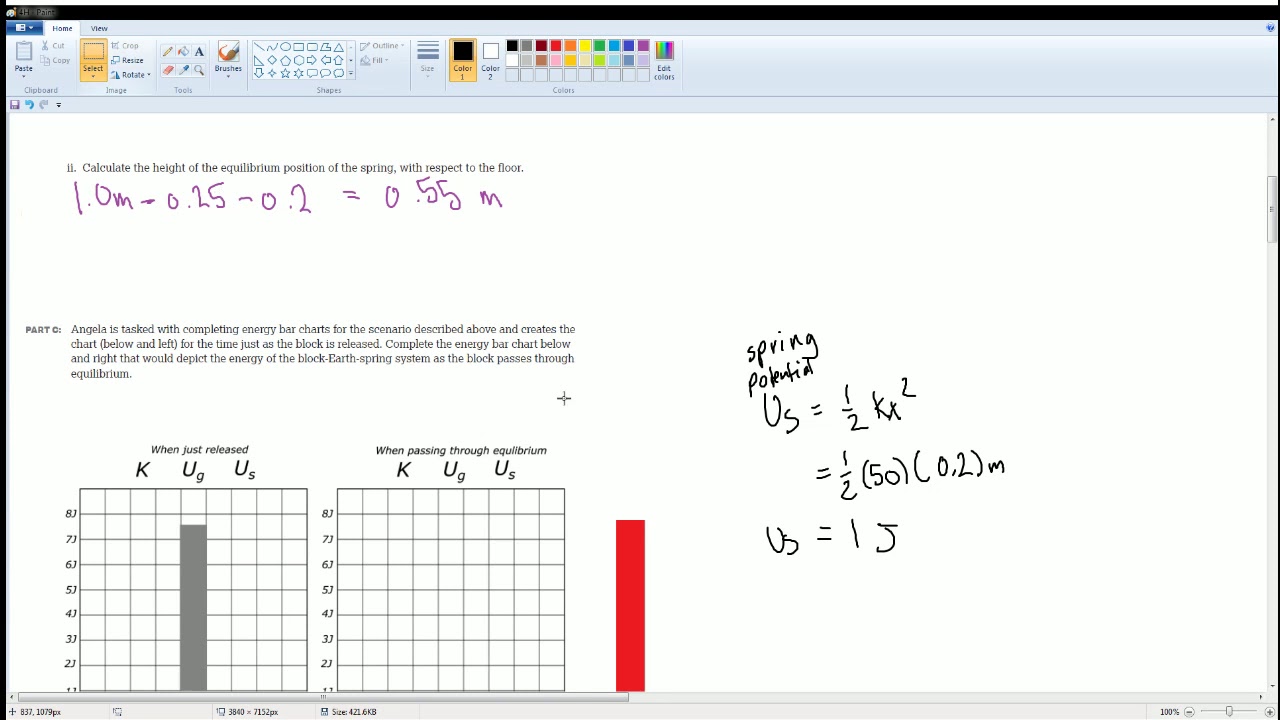
AP Physics Workbook 4.H Potential Energy and Choice of Zero

Conservation of Energy Physics Problems

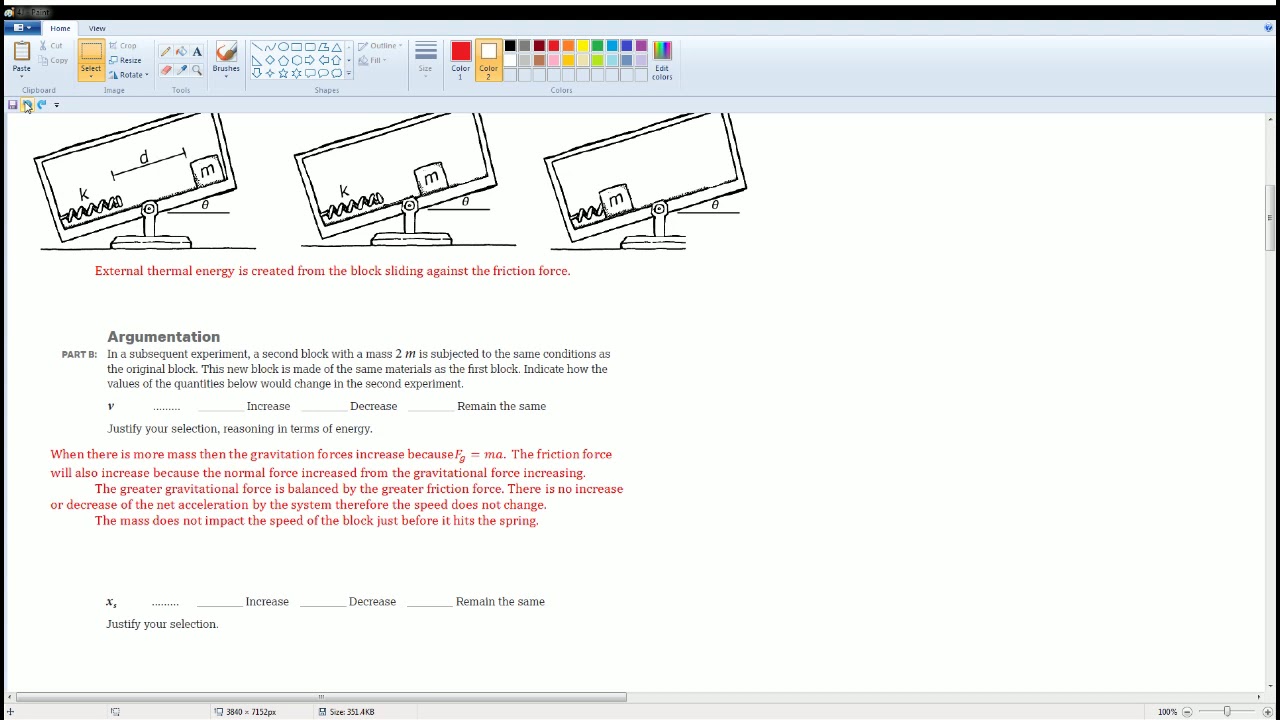
AP Physics Workbook 4.J Impact of Mass on Conservation of Energy

'AP Physics 2023 Exam Solutions|Q1. PART C ( i ) | Complete Step-by-Step Answers and Explanations"

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsEnergy TransformationMechanical SystemsSpring DynamicsKinetic EnergyPotential EnergyFrictional ForcesWork and EnergyConservation LawsEducational Content