2015 #3 Free Response Question - AP Physics 1 - Exam Solution
TLDRIn this engaging physics problem-solving session, the discussion revolves around a block-spring system and its energy transformations. Starting with the block at the equilibrium position, the scenario explores the block's kinetic and potential energies as it moves from a compressed state to a frictionless and then a frictional surface. The session clarifies misconceptions about the relationship between the spring's compression and the block's stopping distance, emphasizing the non-linear nature of elastic potential energy and the work done by friction. The problem culminates in deriving an expression for the block's new final position when the spring is compressed twice as much, highlighting the importance of quantitative reasoning in physics.
Takeaways
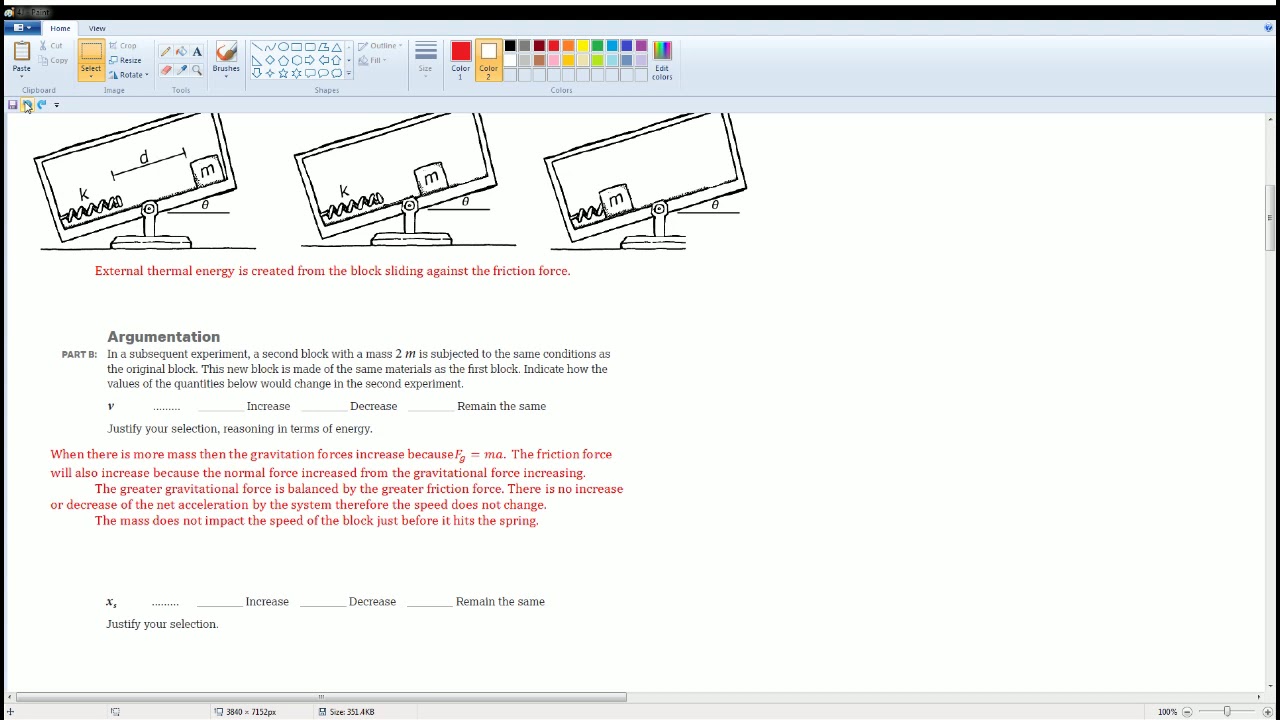
- 📌 The problem involves a block-spring system with a frictionless surface initially, then a frictional section.
- 📈 The task is to sketch graphs of kinetic energy (KE) and potential energy (U) as functions of the block's position from x = -D to x = +3D.
- 🌐 At the start (x = -D), the block has maximum potential energy and zero kinetic energy.
- 🔄 As the block moves from x = -D to x = 0 (equilibrium), potential energy converts to kinetic energy, with the latter peaking at equilibrium.
- 🚫 When the block enters the frictional section, mechanical energy is no longer conserved due to work done by friction.
- 📉 The kinetic energy decreases linearly from equilibrium to the final stop due to the constant force of kinetic friction.
- 🔧 The initial mechanical energy at the start of the frictional section is equal to the initial potential energy (1/2 kD^2).
- 📌 The student's reasoning that more compression leads to a farther slide is correct, but the assumption of a linear relationship (twice the distance) is incorrect.
- 🔢 The mathematical relationship derived shows that the final displacement with twice the compression is four times the original (12D instead of 6D).
- ✅ The correct mathematical model accounts for the non-linear relationship between the spring's potential energy and the displacement.
Q & A
What is the initial condition of the block in the problem?
-The block is initially located at position zero, which is the equilibrium position for the spring, and it is at rest.
How does the block's kinetic energy change as it moves from the compressed spring to the equilibrium position?
-The block's kinetic energy increases as it moves from the compressed spring (x equals negative D) to the equilibrium position (x equals zero) because the elastic potential energy is converted into kinetic energy. At the equilibrium position, the kinetic energy reaches its maximum value, equal to the initial potential energy.
What happens to the mechanical energy of the system when the block encounters friction?
-When the block encounters friction, the mechanical energy of the system is no longer conserved. The kinetic energy is converted into heat and sound due to the work done by the frictional force, until the block comes to a stop.
How does the friction affect the block's motion from the equilibrium position to the final stop?
-The friction causes a linear decrease in the block's kinetic energy as it slides from the equilibrium position to the final stop at three times the distance D from the equilibrium position. The work done by friction is proportional to the displacement, leading to a stop when all the initial mechanical energy is used up.
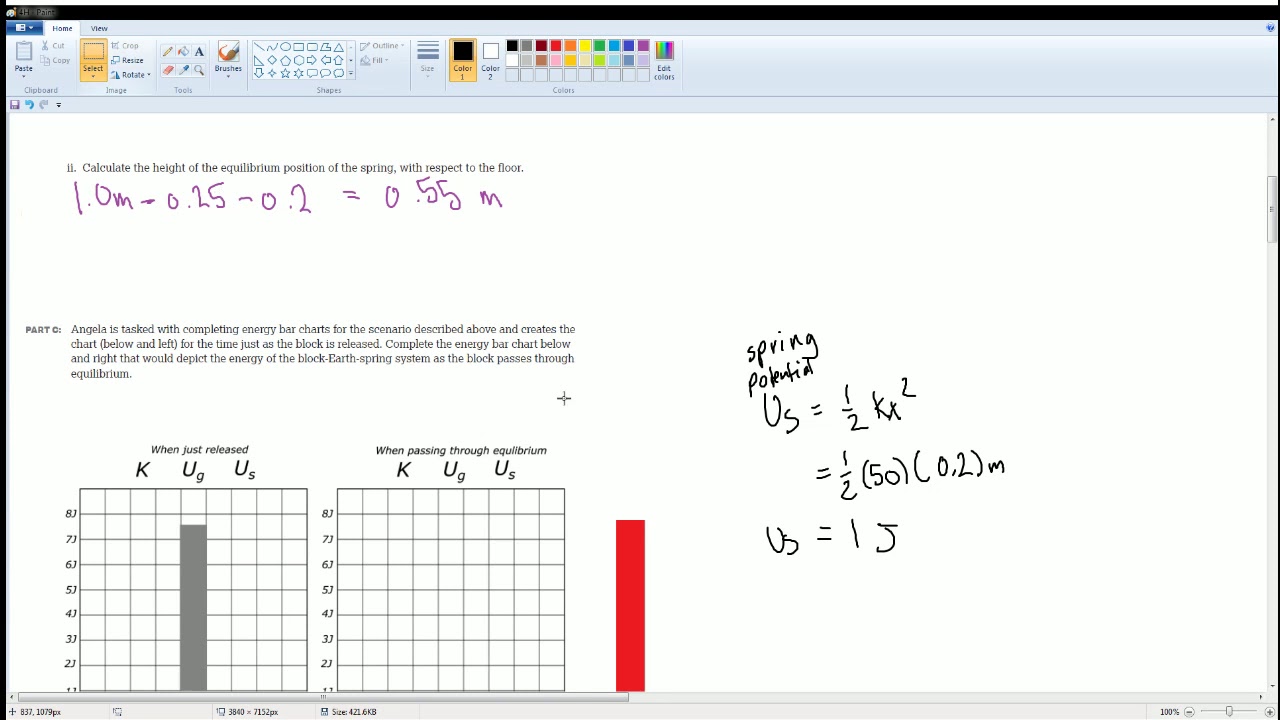
What is the relationship between the spring's compression and the elastic potential energy stored?
-The elastic potential energy stored in the spring follows the equation one-half times the spring constant (k) times the displacement from the equilibrium position (x) squared. So, if the spring is compressed twice as much, the stored potential energy increases by a factor of the square of two, not twofold.
What is the student's prediction regarding the final position of the block when the spring is compressed twice as much?
-The student predicts that the block will stop at a position twice as far (x equals six-D) when the spring is compressed twice as much. However, this prediction does not account for the non-linear relationship between the spring's compression and the potential energy stored.
How does the actual final position of the block compare to the student's prediction?
-The actual final position of the block is not twice as far as the original stop point. Instead, it is four times as far (12 times capital D) due to the non-linear relationship between the spring's compression and the potential energy stored.
What mathematical expression can be used to calculate the new final position of the block?
-The new final position (displacement two) can be calculated using the expression: Displacement two equals four times the spring constant times capital D-squared, divided by the quantity two times the Force of Kinetic Friction.
How does the mathematical reasoning in part c correct the student's incorrect assumption?
-The mathematical reasoning shows that the increase in the stopping distance is not linear but proportional to the square of the increase in the spring's compression. This corrects the student's assumption that the distance would double when the spring's compression doubles.
What is the significance of including zero values on the graph in the problem?
-Including zero values on the graph is important because it accurately represents the state of the system at different points, even if certain quantities like elastic potential energy or kinetic energy are zero at those points. This ensures the graph is a complete representation of the system's energy changes.
How does the work done by friction relate to the change in mechanical energy?
-The work done by friction is equal to the change in mechanical energy. When friction is acting on the block, it does work that is proportional to the displacement and converts the block's kinetic energy into heat and sound, leading to a decrease in mechanical energy until the block stops.
Outlines
📚 Solving AP Physics 1 Free Response Question
The video begins with an introduction to solving Free Response Question number 3 from the 2015 AP Physics 1 exam. The scenario involves a block and a spring, where the block is initially at the equilibrium position and compresses the spring by a distance D. The block then slides on a frictionless surface until it hits a rough part of the track and eventually stops at a distance of 3D from the equilibrium position. The task is to sketch graphs of the kinetic energy (KE) and potential energy (U) of the block-spring system as a function of its position, from x = -D to x = +3D. The video emphasizes the importance of direction in energy calculations and the conservation of mechanical energy on the frictionless surface. The initial maximum potential energy is calculated as (1/2)kD^2, and it is converted into kinetic energy as the block moves towards the equilibrium position. The presence of friction on the rough surface leads to a linear decrease in kinetic energy, with the potential energy being zero from 0 to +3D since the spring is no longer compressed.
🔍 Analyzing Student's Reasoning on Energy Conservation
This section of the video discusses a student's reasoning about the effect of compressing the spring twice as much on the final position of the block. The student believes that the block will stop twice as far due to the increased energy when the spring is released. The video corrects this misconception by explaining that the elastic potential energy stored in the spring follows a quadratic relationship with displacement (1/2kx^2), not a linear one. The new final position is derived quantitatively by equating the work done by friction to the change in mechanical energy. The block's final stoppage is calculated to be at 12D, which is four times the original distance, demonstrating that the increase in distance is proportional to the square of the increase in potential energy, not linearly.
📈 Relating Mathematical Relationships to Student's Reasoning
The final part of the video ties the mathematical relationships developed in the previous section to the student's reasoning. It confirms that the student's intuition about the block having more energy and sliding farther is correct but clarifies that the relationship is not linear. The new elastic potential energy is twice the original, leading to a greater amount of work done by friction to stop the block, thus increasing the displacement. However, this increase is squared, not linear, as the energy stored in the spring is proportional to the square of the displacement. The mathematical reasoning corrects the student's misconception about the linear relationship between the distance compressed and the final stopping position.
Mindmap
Keywords
💡Free Response Question
💡Block
💡Spring
💡Friction
💡Mechanical Energy
💡Kinetic Energy
💡Potential Energy
💡Conservation of Energy
💡Graphs
💡Displacement
💡Work-Energy Theorem
Highlights
The problem involves a block-spring system and its interaction with frictionless and frictionful surfaces.
The block is initially at the equilibrium position of the spring and is then compressed and released.
The block slides back to the equilibrium position where it encounters a rough, frictionful part of the track.
The task is to sketch graphs of kinetic energy and potential energy as a function of
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: