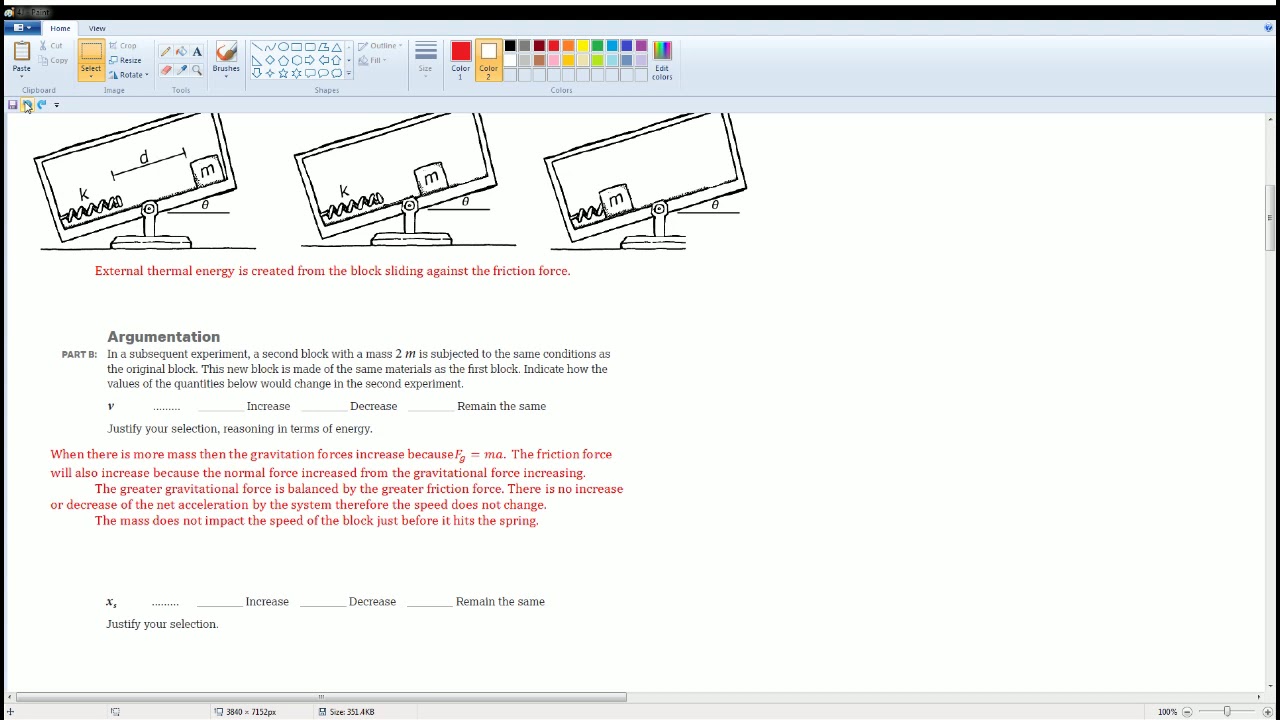
2015 AP Physics 1 free response 3b
TLDRThe video script explores a student's reasoning about the relationship between the compression of a spring and the resulting motion of a block. The student believes that compressing the spring twice as much would double the block's final position, but the correct analysis shows that it would actually result in a quadruple stopping distance due to the square relationship between compression and potential energy.
Takeaways
- 📈 The spring's compression increases from D to 2D, doubling the potential energy stored.
- 🔄 The potential energy is converted into kinetic energy when the spring releases the block.
- 🚫 The student's assumption that the block will stop exactly at 6D is incorrect due to the nature of energy conversion and friction.
- 🔄 In the first scenario, the block's kinetic energy is converted to heat due to friction, stopping it after 3D.
- 🔄 In the second scenario, the block is expected to have more kinetic energy due to the greater compression of the spring.
- 📊 The potential energy (PE) of a spring is given by PE = 1/2 * spring constant * compression^2.
- 🔢 Doubling the spring's compression results in a quadrupling of potential energy (2^2 = 4).
- 🏁 The stopping distance is not simply doubled, but quadrupled due to the increased energy.
- 🧠 The student's reasoning is partially correct; more energy does result in a longer stopping distance, but not exactly doubled.
- 🔄 The process involves energy transformations: potential to kinetic, and kinetic to heat due to friction.
- 📚 The problem illustrates the principles of conservation of energy and the effects of friction on motion.
Q & A
What is the initial condition described in the script?
-The initial condition is that the spring is compressed by a distance D, which is the first scenario the student is asked to consider.
How does the potential energy stored in the spring get converted?
-The potential energy stored in the spring gets converted into kinetic energy as the spring releases and the block accelerates.
What happens to the kinetic energy of the block as it moves along the track?
-The kinetic energy of the block is gradually converted into heat due to the action of friction, which eventually causes the block to stop.
What is the student's prediction for the second scenario where the spring is compressed twice as much?
-The student predicts that the block will slide farther, stopping at a position x equals 6D, because the spring has more potential energy when compressed twice as much.
What is the relationship between the compression of the spring and the potential energy stored?
-The potential energy stored in the spring is proportional to the square of the compression distance, meaning that compressing the spring twice as much results in four times the potential energy.
What is the student's reasoning about the stopping distance in the second scenario?
-The student reasons that since there is more potential energy in the second scenario, the block will travel exactly twice as far, stopping at 6D.
What is the correct relationship between the compression distance and the stopping distance?
-The correct relationship is that compressing the spring twice as much does not result in exactly twice the stopping distance; it actually results in four times the stopping distance due to the square relationship between compression and potential energy.
How does the friction force affect the block's motion?
-The friction force acts against the motion of the block, providing negative work and causing the block to slow down and eventually stop.
What is the role of the spring constant in determining the potential energy?
-The spring constant, denoted as k, is a factor in the formula for potential energy, which is given by 1/2 * k * (compression distance)^2. A larger spring constant would result in more potential energy for a given compression distance.
What is the significance of the block's final position in understanding the scenario?
-The block's final position is significant because it indicates where the balance between the potential and kinetic energy, and the work done by friction, results in the block coming to a stop.
How does the script illustrate the concept of energy conservation?
-The script illustrates energy conservation by showing how potential energy is converted into kinetic energy, and then into heat due to friction, without an external loss or gain of energy in the system.
Outlines
🔍 Analysis of Student's Reasoning on Spring Compression and Block Motion
This paragraph discusses a student's reasoning regarding the effect of spring compression on the motion of a block. The student posits that compressing the spring twice as much would result in the block traveling twice as far. The analysis includes a review of the initial scenario where the spring was compressed by D and the block's subsequent motion due to the conversion of potential energy to kinetic energy, and the role of friction in stopping the block. The student then extrapolates this understanding to predict that a greater compression (2D) would lead to more potential energy, more kinetic energy at the point of release, and thus a greater stopping distance. However, the paragraph ends with a question mark, indicating uncertainty about the accuracy of this prediction.
📈 Correct and Incorrect Aspects of Student's Reasoning on Energy and Stopping Distance
This paragraph evaluates the correctness of the student's reasoning from the previous discussion. It confirms that the student is correct in asserting that compressing the spring more would result in more energy when the block leaves the spring, leading to a longer stopping distance. However, it corrects the misconception that compressing the spring twice as much would result in exactly twice the stopping distance. The explanation is grounded in the mathematical relationship that potential energy is proportional to the square of the compression, suggesting that twice the compression would lead to four times the energy and, consequently, four times the stopping distance. This paragraph provides a clear and detailed analysis of the principles of energy transformation and friction that govern the block's motion.
Mindmap
Keywords
💡spring
💡compressed
💡potential energy
💡kinetic energy
💡block
💡friction
💡work
💡energy conversion
💡stopping distance
💡spring constant
💡negative work
Highlights
The spring is compressed twice as much, to delta x equals 2D.
Student predicts the final position of the block will be twice as far at x equals 6D.
The block has more energy when it leaves the spring, due to increased compression.
The block slides farther along the track before stopping at position x equals 6D.
In the first scenario, the spring is compressed by D and then accelerates the block.
Potential energy is converted into kinetic energy when the spring is compressed and released.
Friction provides negative work, acting against the motion of the block.
The kinetic energy of the block is eventually converted into heat, causing it to stop.
In the new scenario, the spring is compressed twice as far, to x equals negative 2D.
More potential energy results from greater compression of the spring.
The potential energy is converted to kinetic energy upon reaching x equals zero.
The block is expected to travel further due to the increased potential energy.
The student's reasoning is partially correct; more energy does result in a longer stopping distance.
However, the student's assumption that the stopping distance will exactly double is incorrect.
Potential energy is calculated as 1/2 times the spring constant times the compression squared.
Doubling the compression results in four times the potential energy, not double.
The stopping distance increases by a factor of four, not two.
The explanation clarifies both the correctness and the incorrectness of the student's reasoning.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: