Residual Plot on TI-84 Plus

Shawn Burke
11 Feb 202204:28
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial demonstrates how to create a residual plot on a graphing calculator, emphasizing the importance of having data entered and a linear regression model calculated. It guides viewers through the process of checking data in lists L1 and L2, using the calculator's statistical features to perform linear regression and generate residuals. The video then instructs on plotting these residuals against the X values from the data, to evaluate the fit of the linear model. The final step involves adjusting the graph settings to display the residual plot without the line of best fit, allowing for an assessment of the model's appropriateness. The clear and concise explanation is aimed at viewers with a basic understanding of statistics and algebra.

Takeaways
  • ๐Ÿ“Š Familiarize yourself with the stat menu and data entry process on the graphing calculator for statistical analysis.
  • ๐Ÿ“ˆ Ensure your data is correctly entered in lists L1 and L2 before proceeding with residual plot creation.
  • ๐Ÿ” Verify that a stat scatter plot has been created to visualize the data points and their distribution.
  • ๐Ÿ“ Understand the necessity of a linear regression model (using option 8 for the format) for calculating residuals.
  • ๐Ÿ‘๏ธ Use the calculator's summary statistics to obtain the y-intercept, slope, coefficient of determination, and correlation.
  • ๐Ÿ”ข Store the linear regression equation in Y1 for easy reference and analysis using tables and graph menu.
  • ๐Ÿงฉ Access the list of residuals by navigating to the stat menu and selecting option number seven.
  • ๐Ÿ“Š To create a residual plot, adjust the graphing calculator's stat plot menu to use the residuals list (option number seven) instead of the original Y values.
  • ๐Ÿšซ Turn off the line of best fit in the residual plot by editing the Y= equation to simply press enter.
  • ๐Ÿ“Š The residual plot should have a sum of residuals close to zero, which is an indicator of the model's fit.
  • ๐Ÿค” Use the residual plot to assess the appropriateness of the linear fit for the given data set.
Q & A

  • What is the primary purpose of the video?

    -The primary purpose of the video is to demonstrate how to create a residual plot on a graphing calculator.

  • Where should the data for the residual plot be entered on the calculator?

    -The data for the residual plot should be entered in lists L1 and L2 on the calculator.

  • How can you check if your data is correctly entered and plotted?

    -You can check if your data is correctly entered and plotted by hitting 'zoom 9' to view your scatter plot of the data.

  • What is required before creating a residual plot?

    -A linear regression model is required before creating a residual plot, as residuals are calculated based on this model.

  • Which option should be used for the linear regression model in a statistics class?

    -In a statistics class, option 8 should be used for the linear regression model where the constant is placed first followed by the x term.

  • How do you store the linear regression equation on the calculator?

    -The linear regression equation is typically stored in Y1 by using the 'vars' button, going to the right, hitting 'Y vars', and then 'Y equals'.

  • What statistics are provided after calculating the linear regression model?

    -After calculating the linear regression model, you are provided with summary statistics including the Y-intercept, slope, coefficient of determination, and correlation.

  • How can you view the list of residuals on the calculator?

    -You can view the list of residuals on the calculator by hitting the 'second' button, then 'stat', and selecting option number seven.

  • What change needs to be made to the Y list when plotting a residual plot?

    -When plotting a residual plot, the Y list should be changed from the individual values of Y to the residuals.

  • How do you remove the line of best fit from the residual plot?

    -To remove the line of best fit from the residual plot, you can go into the 'Y equals' menu, tap on the equal sign, and hit enter.

  • What can the residual plot help you determine?

    -The residual plot can help you determine whether or not the linear fit is appropriate for the data.

Outlines
00:00
๐Ÿ“Š Creating a Residual Plot on a Graphing Calculator

This paragraph explains the process of creating a residual plot using a graphing calculator. It begins by emphasizing the importance of having data entered in the stat menu and having a stat scatter plot prepared. The speaker then guides the viewer through the steps of performing a linear regression by accessing the calc option and choosing the appropriate settings for the algebra or statistics class. The paragraph further discusses the storage of the regression equation in y1 for easy reference and analysis. The summary statistics obtained from the calculator, including the y-intercept, slope, coefficient of determination, and correlation, are explained. Finally, the paragraph details how to view and plot the list of residuals, and how to adjust the stat plot menu to graph the residual plot, including turning off the line of best fit for clearer analysis.

Mindmap
Keywords
๐Ÿ’กresidual plot
A residual plot is a graphical tool used in statistics to diagnose the appropriateness of a linear regression model by comparing the differences (residuals) between the observed values and the values predicted by the model. In the video, the residual plot is created using a graphing calculator to evaluate the fit of the model, with the residuals being the focus of the plot rather than the original data points. This helps in identifying any patterns or inconsistencies that might suggest a problem with the linear model.
๐Ÿ’กgraphing calculator
A graphing calculator is an electronic device used to perform mathematical calculations, including graphing functions and creating visual representations of data. In the context of the video, it is used to input data, perform linear regression analysis, and generate both scatter plots and residual plots, which are essential tools for statistical analysis.
๐Ÿ’กdata entry
Data entry refers to the process of inputting data into a system or device, such as a graphing calculator or a computer program. In the video, data entry involves entering statistical data into the calculator's memory (L1 and L2) to prepare for the creation of a scatter plot and subsequent residual plot.
๐Ÿ’กlinear regression model
A linear regression model is a statistical method used to model the relationship between a dependent variable and one or more independent variables by fitting a linear equation to the observed data. In the video, the linear regression model is essential for generating residuals, which are the differences between the actual data points and the points predicted by the model.
๐Ÿ’กscatter plot
A scatter plot is a type of graph used to display values for two variables for a set of data. It uses dots to represent each data point, showing the relationship between the variables. In the video, a scatter plot is initially created to visualize the data before generating a residual plot to assess the fit of the linear regression model.
๐Ÿ’กresiduals
Residuals are the differences between the observed values and the values predicted by a statistical model, such as a linear regression. They are a measure of the model's accuracy and can reveal patterns or discrepancies that might indicate a problem with the model's assumptions. In the video, residuals are calculated by the graphing calculator and then plotted to evaluate the linear fit.
๐Ÿ’กy-intercept
The y-intercept is the point at which a line crosses the y-axis in a two-dimensional Cartesian coordinate system. In the context of a linear regression model, it represents the value of the dependent variable when the independent variable is zero. The video mentions the y-intercept as part of the summary statistics provided by the calculator when performing linear regression.
๐Ÿ’กslope
The slope of a line in a two-dimensional Cartesian coordinate system represents the rate of change between the dependent variable and the independent variable. In a linear regression model, the slope indicates the direction and steepness of the line, which describes the relationship between the variables. The video mentions a slope of approximately negative 8.9, which suggests that the dependent variable decreases as the independent variable increases.
๐Ÿ’กcoefficient of determination
The coefficient of determination, often denoted as R-squared (Rยฒ), is a statistical measure that represents the proportion of the variance in the dependent variable that is predictable from the independent variable(s). It provides an indication of how well the observed outcomes are replicated by the model. In the video, a high R-squared value of about 9.94 suggests that the linear model explains a significant portion of the variance in the data.
๐Ÿ’กcorrelation
Correlation is a statistical term that describes the degree to which two or more variables are related or move together. A high positive correlation indicates that as one variable increases, the other also increases, while a high negative correlation indicates that as one variable increases, the other decreases. In the video, a correlation of about negative 0.97 suggests a strong inverse relationship between the variables in the data set.
๐Ÿ’กlist L1 and L2
In the context of the video, list L1 and L2 refer to the specific lists or memory locations on a graphing calculator where the user inputs their data for statistical analysis. L1 typically holds the values for the independent variable (x-values), while L2 holds the values for the dependent variable (y-values). These lists are essential for creating scatter plots, linear regression models, and residual plots.
๐Ÿ’กzoom 9
In the context of a graphing calculator, 'zoom 9' is a command that allows users to view the entire range of their graph or data plot on the screen. This function is useful for getting a comprehensive view of the data or the regression line and is used in the video to quickly inspect the scatter plot and residual plot.
Highlights

The video demonstrates how to create a residual plot on a graphing calculator.

Ensure data is entered in the stat menu, specifically in lists L1 and L2.

Verify that a stat scatter plot has been created for quick data visualization.

A linear regression model is necessary for creating a residual plot.

For a typical algebra class, use the y = mx + b form, while statistics often use the form with the constant first.

Store the linear regression equation in Y1 for easy access and analysis.

The calculator provides summary statistics including the y-intercept, slope, coefficient of determination, and correlation.

The calculator automatically generates a list of residuals based on the entered data.

View the list of residuals by accessing the stat menu and selecting option number seven.

To plot the residuals, change the Y list in the stat plot menu from individual y values to the residuals list.

After plotting, the line of best fit may still appear and can be removed by editing the Y= equation.

The residual plot allows for the assessment of the appropriateness of the linear fit.

The process may seem tedious but is essential for working with graphing calculators in statistical analysis.

The video provides a step-by-step guide, making it accessible for users to follow along and apply to their own data.

The use of the calculator for statistical analysis is a practical application in algebra and statistics classes.

The video concludes by thanking the viewers for their attention, emphasizing the value of the information shared.

Transcripts

Browse More Related Video

Calculating Residuals & Making Residual Plots on TI-84 Plus

How to Calculate the Residual

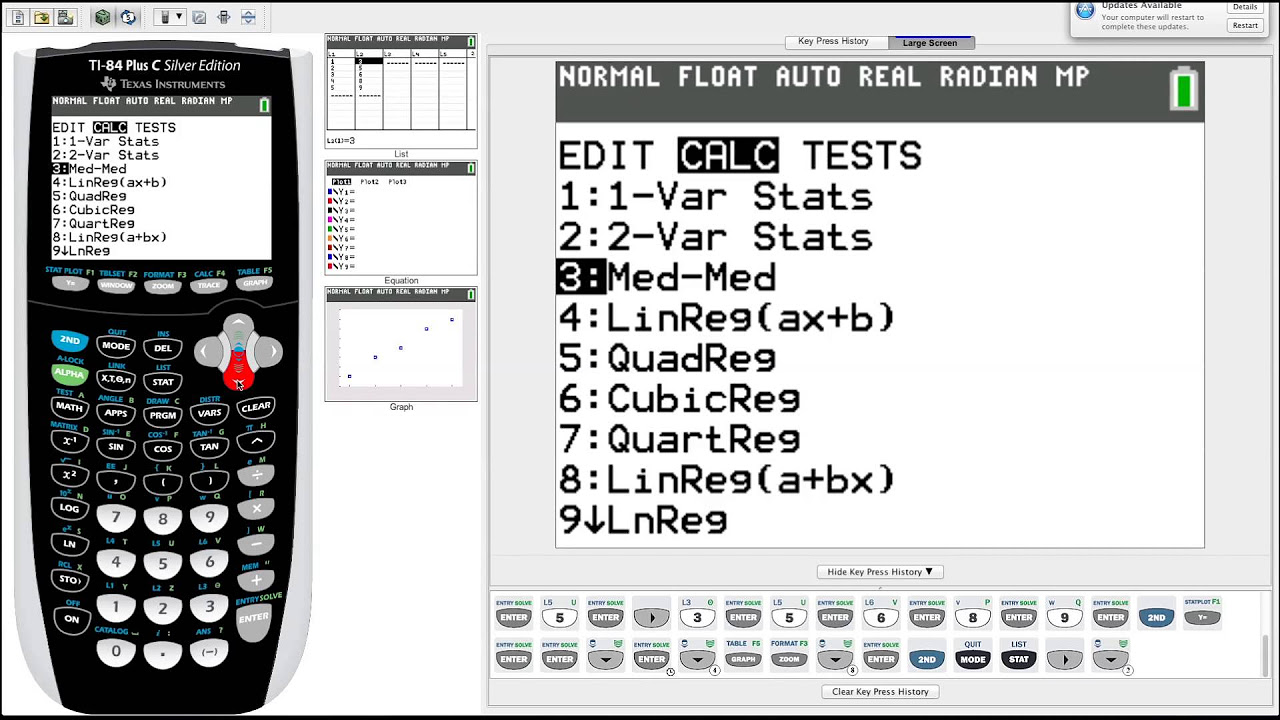
TI-84 Plus Graphing Calculator Guide: Statistics

Residual plots | Exploring bivariate numerical data | AP Statistics | Khan Academy

Pre-Calculus - Find the linear regression line using the TI-83/84 calculator (2)

Statistics 101: Linear Regression, Residual Analysis

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Residual PlotGraphing CalculatorStatistical AnalysisData AccuracyLinear RegressionEducational TutorialMathematics ClassTech GuidePlot InterpretationStatistical Tools