8.01x - Lect 5 - Circular Motion, Centripetal Forces, Perceived Gravity
TLDRIn this engaging lecture, the concept of uniform circular motion is explored, detailing the principles of velocity, centripetal acceleration, and the role of centripetal force in maintaining circular paths. The demonstration of a rotating vacuum cleaner's high acceleration, the separation of particles in a centrifuge, and the illusion of altered gravity through rotation are highlighted. The lecture also touches on the application of these principles in everyday scenarios and scientific experiments, offering a fascinating insight into the physics governing motion in a circle.
Takeaways
- 🌀 Uniform circular motion involves an object moving in a circle with a constant speed, but changing velocity due to direction change.
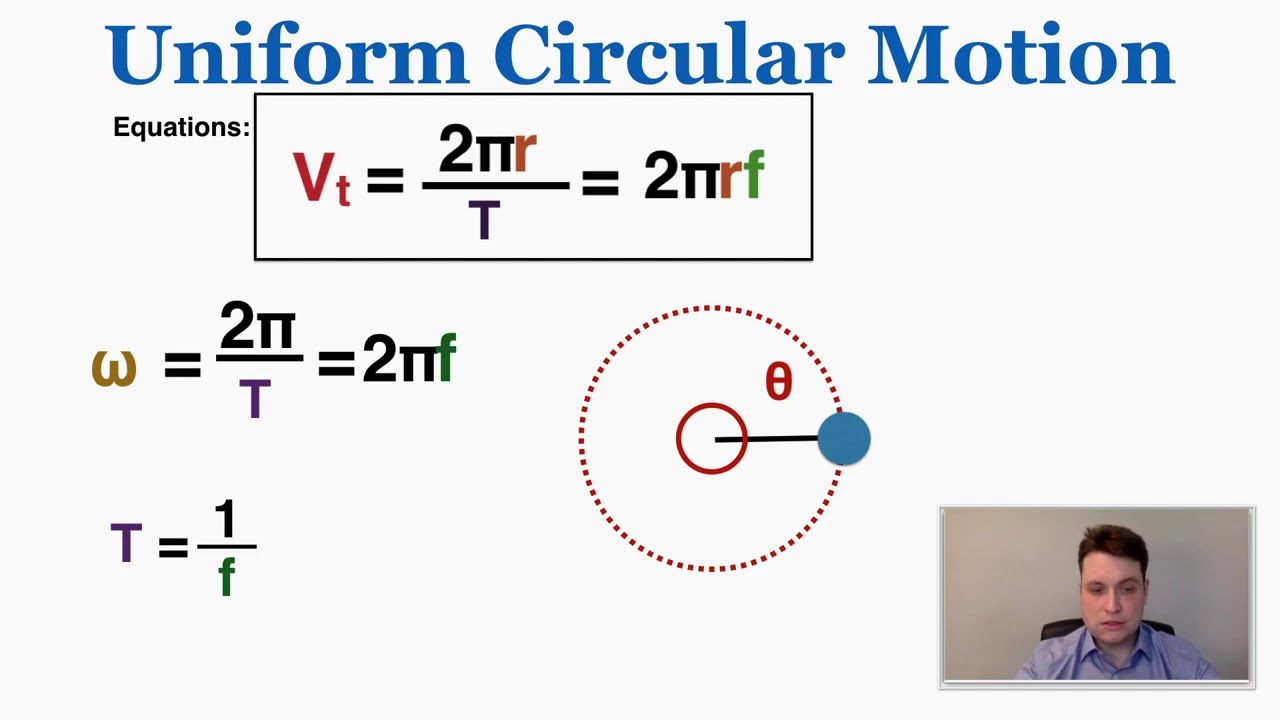
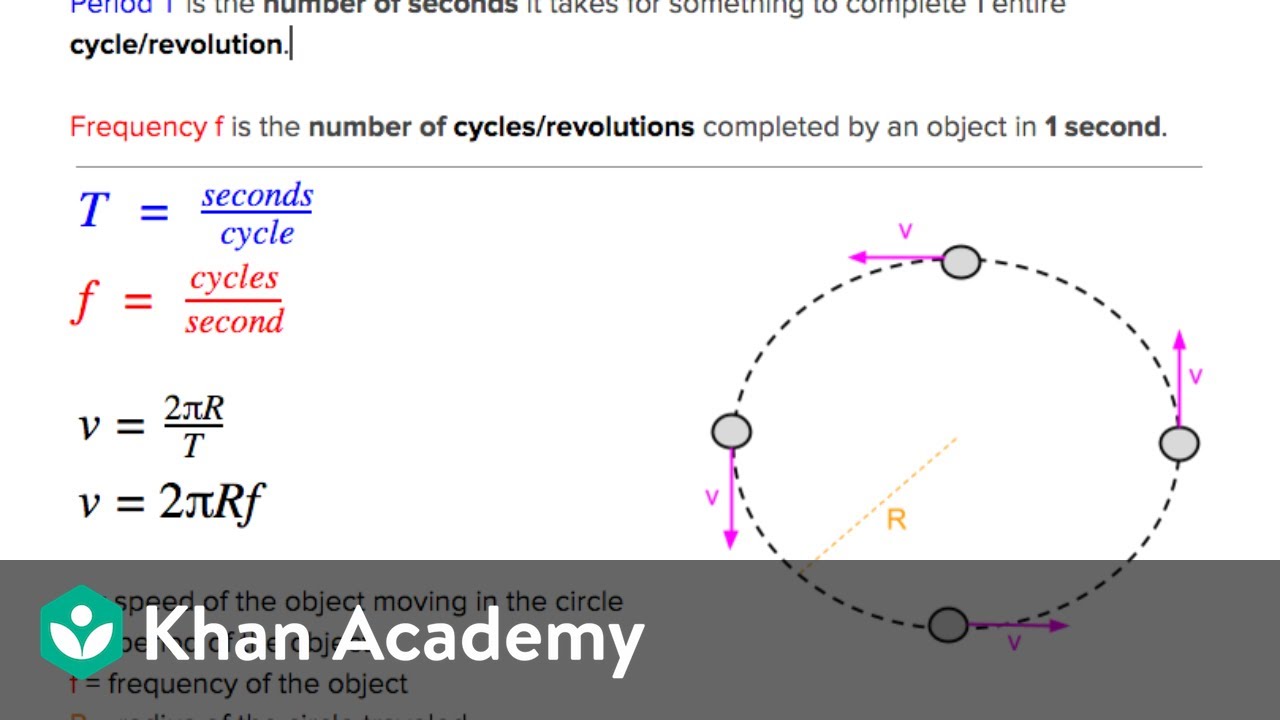
- 🔄 The period (T) is the time taken for one complete revolution, while frequency (f) is the number of revolutions per second, measured in hertz.
- 📐 Angular velocity (omega) is the rate of rotation in radians per second, and it's related to the period by the formula omega = 2π / T.
- 🏃♂️ Centripetal acceleration is the acceleration directed towards the center of the circle, with a magnitude of v^2 / r or omega^2 * r.
- 🚫 Without a centripetal force, an object in circular motion would move in a straight line tangent to the circle at the release point.
- 🧱 A vacuum cleaner's rotor demonstrates centripetal acceleration, with its scoops experiencing an acceleration much greater than gravity's acceleration.
- 🌍 Planetary motion around the sun is influenced by gravity providing the necessary centripetal force, with the sun's gravitational pull affecting the planets.
- 📉 Centripetal acceleration is inversely proportional to the square of the distance from the center of rotation (R^2 law).
- 🔄 A centrifuge uses high-speed rotation to separate substances of different densities by simulating a strong gravitational effect.
- 🛀 The direction of perceived gravity in a rotating system is opposite to the direction of the centripetal force acting on the object.
- 🥦 Lewin's grandmother's method of spinning lettuce to dry it uses the same principle as a centrifuge, demonstrating the practical application of physics in everyday life.
Q & A
What is uniform circular motion?
-Uniform circular motion is when an object moves in a circle at a constant speed, meaning the magnitude of the velocity does not change, but its direction does. The object covers equal arc lengths in any equal intervals of time.
What is the relationship between angular velocity (omega) and the period (T)?
-Angular velocity (omega) is related to the period (T) by the equation omega equals two pi divided by T. This means that omega measures the number of radians per second and is directly related to how quickly the object completes one full rotation, which is the period T.
How is centripetal acceleration related to velocity and radius?
-Centripetal acceleration is related to velocity (v) and radius (r) by the formula a_c = v^2 / r. It represents the acceleration that keeps an object moving in a circular path and is always directed towards the center of the circle.
What is the significance of the vacuum cleaner example in explaining uniform circular motion?
-The vacuum cleaner example illustrates the concepts of angular velocity, centripetal acceleration, and the significant forces involved in uniform circular motion. It shows how the scoops, moving at a high speed, experience a large centripetal acceleration, even though the vacuum cleaner itself may appear stationary to an observer.
How does the direction of centripetal acceleration change?
-The direction of centripetal acceleration always points towards the center of the circular path. This is necessary for maintaining the object's circular motion, as it constantly changes the direction of the velocity vector.
What is the 'one over R square' law in physics?
-The 'one over R square' law, also known as the inverse-square law, states that a quantity is inversely proportional to the square of the distance from a central point. In the context of the script, it refers to the gravitational force and centripetal acceleration experienced by planets, which decrease with the square of the distance from the Sun.
How does the experiment with the rotating bucket of water demonstrate the concept of perceived gravity?
-The rotating bucket of water experiment demonstrates that the perceived direction of gravity can change based on the centripetal acceleration experienced by an object. When the bucket is rotated fast enough, the water perceives gravity as being towards the ceiling, even though the actual gravitational force is still acting downwards, causing the water to stay in the bucket when it is upside down.
What is the role of centripetal force in maintaining uniform circular motion?
-Centripetal force is the net force acting on an object in uniform circular motion, directed towards the center of the circle. It is responsible for the necessary centripetal acceleration that keeps the object moving in a circular path, changing the direction of the velocity without altering its magnitude.
How does the script use the concept of uniform circular motion to explain the behavior of planets around the Sun?
-The script uses the concept of uniform circular motion to explain that planets orbit the Sun due to the gravitational pull, which acts as the centripetal force needed for their circular paths. The different distances and periods of the planets result in different angular velocities and centripetal accelerations, following the 'one over R square' law.
What is the practical application of the centrifuge demonstrated in the script?
-The script demonstrates the practical application of a centrifuge in separating substances of different densities. By spinning a mixture of saltwater and silver nitrate at high speeds, the denser silver chloride particles are forced towards the sides and bottom of the container, effectively separating them from the liquid.
Outlines
🔄 Introduction to Uniform Circular Motion
The paragraph introduces the concept of uniform circular motion, where an object moves in a circle with a constant speed. It explains the difference between speed and velocity, emphasizing that while speed remains constant, the direction of velocity changes, indicating a change in motion that necessitates acceleration. The paragraph introduces the period (T), frequency (f), and angular velocity (omega), and their interrelationships. It also explains the concept of centripetal acceleration, which is always directed towards the center of the circle, and provides equations to calculate it using velocity and angular velocity. The example of a vacuum cleaner's rotor illustrates these concepts, showing how the centripetal acceleration can be significant even in everyday objects.
🌀 Centripetal Acceleration and its Causes
This paragraph delves deeper into the concept of centripetal acceleration, explaining its magnitude and how it is related to the radius of the circular path and the velocity of the object. It clarifies the misconception that centripetal acceleration is inversely proportional to the radius, using a vacuum cleaner as an example to show that the acceleration is indeed linearly proportional to r. The paragraph then discusses the necessity of a force, either a push or a pull, to maintain circular motion, introducing the idea of centripetal force. It also addresses the common misconception about the motion of an object when the centripetal force is removed, demonstrating through an experiment that the object will move in a straight line rather than a spiral.
🪐 Gravity as the Cause of Centripetal Acceleration in Planetary Motion
The paragraph discusses the application of centripetal acceleration to the motion of planets around the sun. It explains that gravity is the force responsible for the centripetal acceleration experienced by planets in their orbits. The paragraph also touches on the non-uniformity of planetary orbits and the variation in periods and distances of planets from the sun. Using the values for the mean distance and period of planets, the paragraph shows how to calculate the centripetal acceleration for each planet and observes that it falls off as the inverse square of the distance (R^2 law). The paragraph concludes with a demonstration of the concept using a rotating disc and a ball attached to it with a string.
🌌 The Relationship Between Centripetal Acceleration and Distance
This paragraph explores the relationship between centripetal acceleration and the mean distance of planets from the sun, using log paper to plot the data. The slope of the resulting line is found to be very close to -2, indicating that centripetal acceleration decreases with the square of the distance from the sun. The paragraph emphasizes the significance of this 'one over R square' law in physics and how it describes the decrease in gravitational force with distance. It also discusses the hypothetical scenario of removing the sun's gravitational pull, which would result in planets moving in a straight line.
🍴 Everyday Applications of Centrifugal Force
The paragraph discusses the practical applications of centrifugal force in everyday life, such as drying lettuce in a colander and the operation of a centrifuge. It describes the process of drying lettuce by swinging it around, which is an early version of a centrifuge. The paragraph then contrasts this method with a modern, high-tech centrifuge designed for drying salad. It also explains the basic principle behind a centrifuge, where an object's need for centripetal acceleration in a circular motion is met by the push or pull from the surrounding environment, such as the floor of a rotating space station.
🌠 Artificial Gravity and Perceived Direction of Gravity
This paragraph explores the concept of artificial gravity and how it affects the perception of the direction of gravity. It uses the example of a person swinging around on a string to illustrate how the direction of the perceived gravitational pull is opposite to the direction of the actual pull or push. The paragraph further discusses the creation of artificial gravity in a rotating space station, where the centripetal acceleration from rotation is used to mimic the gravitational pull. It explains how the perceived direction of gravity changes with the rotation and how it can be used to create a sense of 'down' in a weightless environment. The paragraph also touches on the challenges of moving from the outer edges to the center of a rotating space station due to the increasing strength of the artificial gravity.
💧 Separation of Mixture Components Using Centrifugal Force
The paragraph describes an experiment that uses centrifugal force to separate components of a mixture. It explains how a centrifuge, with its high rotational speeds, can create a centripetal acceleration much greater than Earth's gravitational acceleration. This increased acceleration causes particles in a mixture to move towards the outer edge of the container, effectively separating them based on their density. The paragraph provides a detailed example of using a centrifuge to separate silver chloride from a mixture with table salt and silver nitrate, resulting in a clear liquid and a side deposit of the heavier particles. It also discusses the precautions needed when designing and using centrifuges due to the high forces involved.
🎢 The Illusion of Gravity in Circular Motion
The paragraph concludes with a demonstration of the illusion of gravity created by circular motion. It describes an experiment where a bucket of water is swung around in a circle, and due to the centripetal acceleration being greater than the acceleration due to gravity, the water remains in the bucket even when it is upside down. The paragraph emphasizes the effectiveness of physics in creating this illusion and encourages the audience to experience it firsthand. It ends with a humorous note, inviting volunteers to try the experiment and ensuring safety precautions are taken.
Mindmap
Keywords
💡Uniform Circular Motion
💡Centripetal Acceleration
💡Angular Velocity (Omega)
💡Centripetal Force
💡Inertia
💡Gravitational Pull
💡Centrifuge
💡Perceived Gravity
💡One Over R Square Law
💡Artificial Gravity
Highlights
Definition of uniform circular motion as an object moving in a circle with constant speed, but changing velocity due to direction change.
Introduction of the period (T) as the time taken for one complete revolution, measured in seconds.
Explanation of frequency (f) as the number of rotations per second, measured in hertz (Hz), and its relationship with the period (T = 1/f).
Definition of angular velocity (omega) as the rate of rotation in radians per second, with the formula omega = 2π/T.
Relationship between linear speed (v), angular velocity (omega), and radius (r), with the formula v = ωr.
Explanation of centripetal acceleration, which is always directed towards the center of the circle, with the formula a_c = v^2/r or a_c = ω^2r.
Example of a vacuum cleaner's rotor to illustrate the concepts of speed, angular velocity, and centripetal acceleration.
Demonstration of the vacuum cleaner's scoops experiencing an acceleration 40 times greater than gravity's acceleration.
Clarification that centripetal acceleration is linear in r and not inversely proportional to it, contrary to common misconceptions.
Discussion on the necessity of a force (pull or push) for an object to undergo circular motion, leading to the concept of centripetal force.
Experiment showing a ball attached to a rotating disc with a string, where cutting the string results in the ball flying off in a straight line.
Explanation of how planets experience centripetal acceleration due to the gravitational pull of the sun, with a focus on the 'one over R square' law.
Illustration of the concept of artificial gravity through the rotation of objects and the resulting centripetal acceleration.
Demonstration of a centrifuge separating substances of different densities by applying centrifugal force.
Experiment showing water staying in an upside-down bucket when rotated at a certain speed, defying the expected gravitational pull.
Discussion on the importance of balancing forces in a centrifuge to prevent damage to the contents due to the high gravitational effects.
Practical application of centrifugal force in drying clothes, and the potential for damage due to the high gravitational effects.
Theoretical application of centripetal acceleration to create artificial gravity in a rotating space station, with implications for living quarters and movement.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: