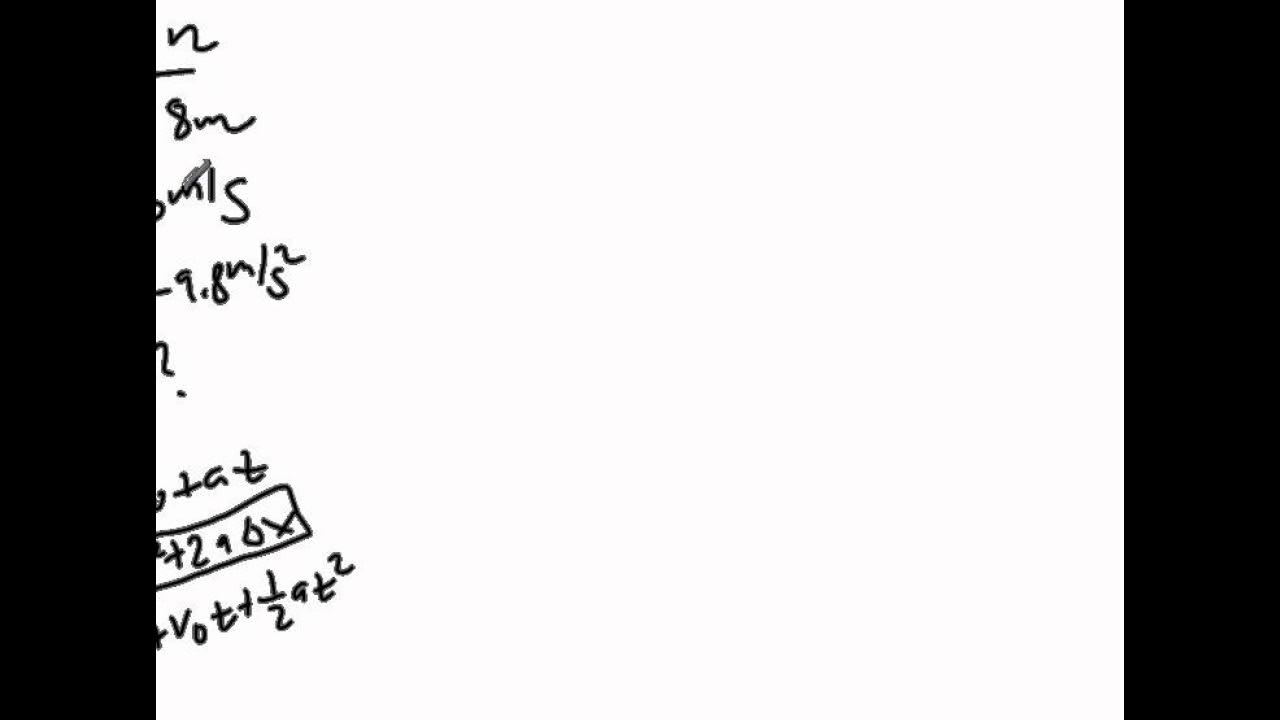Kinematic Equations in One Dimension | Physics with Professor Matt Anderson | M2-04
TLDRIn this educational transcript, Professor Anderson introduces kinematic equations of calculus, emphasizing their importance in understanding motion. The discussion focuses on 1D motion with constant acceleration, leading to the derivation of key equations that relate final position, initial velocity, time, and acceleration. A practical example of a particle in free fall is used to illustrate how velocity and acceleration can be determined from the position function, highlighting the quadratic and linear relationships with time. The concept is applied to free fall near the Earth's surface, where the acceleration due to gravity is -9.8 m/s^2, resulting in a linear increase in speed and quadratic change in position over time.
Takeaways
- 📚 The discussion revolves around kinematic equations of calculus, crucial for analyzing motion.
- 🌟 Kinematic equations are applied to 1D motion, focusing on either horizontal or vertical movement with constant acceleration.
- 🔄 The equations are derived from integrating acceleration (a constant value) to find velocity and integrating again to determine position.
- 📈 The first kinematic equation presented is: x_final = x_initial + v_initial * t + 0.5 * a * t^2.
- 🚀 Another key equation is: v_final = v_initial + a * t, which relates final velocity to initial velocity and time of acceleration.
- 🛫 The third kinematic equation is derived from the others: v_final^2 = v_initial^2 + 2 * a * (x_final - x_initial), which can also be derived from the principle of conservation of energy.
- 📉 A sample problem illustrates a particle in free fall, with its vertical position described by the function y(t) = h - 0.5 * g * t^2.
- 💫 The velocity as a function of time is the derivative of the position function, resulting in v(t) = -g * t.
- 📉 The acceleration in free fall is a constant value, -g, which on Earth is approximately -9.8 m/s^2, indicating that the speed of the falling object increases linearly with time.
- 🔽 The direction of the velocity function (negative value) indicates that the object is moving downward, and its magnitude increases over time.
- 📈 The position function is quadratic, which means the position changes with the square of time, a characteristic of free fall due to gravity.
Q & A
What are kinematic equations?
-Kinematic equations are mathematical formulas used to describe the motion of an object along a straight path, considering its initial position, velocity, acceleration, and time.
Why are kinematic equations important in the study of motion?
-Kinematic equations are crucial in understanding and predicting the behavior of objects in motion, especially in physics and engineering, as they relate variables like position, velocity, and acceleration.
What is the assumption made in the 1D kinematic equations discussed in the transcript?
-The assumption made is that the acceleration is constant, which simplifies the equations and makes them applicable to scenarios where the acceleration does not change over time.
What is the first kinematic equation mentioned in the transcript?
-The first kinematic equation mentioned is x_final = x_initial + v_initial * t + 0.5 * a_x * t^2, which relates the final position (x_final) to the initial position, initial velocity, time, and acceleration.
How is the second kinematic equation derived?
-The second kinematic equation, v_final = v_initial + a_x * t, is derived from one integration of the constant acceleration (a_x), which gives the velocity as a function of time.
What does the third kinematic equation describe?
-The third kinematic equation, v_final^2 = v_initial^2 + 2 * a_x * (x_final - x_initial), describes the relationship between the final and initial velocities, and the change in position, which can also be derived from energy conservation principles.
What is the function y(t) used to describe in the transcript?
-The function y(t) is used to describe the vertical position of a particle as a function of time during free fall, starting from a height h and falling to y equals zero.
How does the velocity function v_y(t) relate to the position function y(t)?
-The velocity function v_y(t) is the derivative of the position function y(t) with respect to time, giving the rate of change of position, which in the case of free fall is negative g * t.
What is the acceleration in free fall due to gravity?
-The acceleration in free fall due to gravity is a constant value of -9.8 meters per second squared (g), indicating that the speed of the falling object increases linearly with time.
How does the position function y(t) change over time?
-The position function y(t) changes quadratically over time, as it is given by h - 0.5 * g * t^2, which shows that the position decreases with the square of time during free fall.
Why does the acceleration due to gravity change with altitude?
-The acceleration due to gravity changes with altitude because it is influenced by the Earth's shape and mass distribution, which causes a slight decrease in gravitational force as you move away from the Earth's surface.
Outlines
📚 Introduction to Kinematic Equations
This paragraph introduces the concept of kinematic equations in the context of calculus, emphasizing their importance in understanding motion. It begins with a discussion on 1D motion, focusing on either horizontal or vertical motion, and highlights the assumption of constant acceleration. The fundamental kinematic equations are presented, including the equation for final position (x final), final velocity (v x final), and the relationship between final velocity squared (v x f squared) and other variables. The paragraph also explains how these equations are derived from the constant acceleration assumption and touches on the application of conservation of energy in deriving one of the kinematic equations.
🚀 Free Fall and Velocity as a Function of Time
The second paragraph delves into a specific example of free fall motion, illustrating how to describe the vertical position (y) of an object as a function of time (t). The function is derived from the kinematic equations, with the negative sign indicating downward curvature and the t squared term suggesting a quadratic relationship. The paragraph corrects the function to account for the initial height (h) from which the object falls. It then explores the concept of velocity as the derivative of position, leading to a linear relationship with time (negative g t). The discussion continues with acceleration, which is the derivative of velocity, and in the case of free fall, it is a constant (minus g). The paragraph concludes by reinforcing the idea that the speed of a falling object increases linearly with time due to gravity, and the position changes quadratically.
Mindmap
Keywords
💡Kinematic Equations
💡Constant Acceleration
💡Free Fall
💡Velocity
💡Acceleration
💡Position
💡Derivative
💡Motion Diagram
💡Energy Conservation
💡Gravity
💡Integration
Highlights
Introduction to kinematic equations of calculus and their importance in studying motion.
Focus on 1D motion, either horizontal or vertical, with constant acceleration.
Kinematic equation for final position: x_final = x_initial + v_initial*t + 0.5*a*t^2.
Derivation of velocity from constant acceleration: v_final = v_initial + a*t.
Kinematic equation derived from energy conservation: v_f^2 = v_i^2 + 2*a*(x_f - x_i).
Illustration of a simple problem involving vertical motion and a particle.
Function y(t) = h - 0.5*g*t^2 to describe the particle's vertical motion.
Velocity as the derivative of position: v_y = dy/dt.
Velocity function v_y(t) = -g*t, indicating a linear increase in speed with time.
Acceleration in free fall is constant and equal to -9.8 m/s^2 near the surface of the Earth.
The position of the falling object changes quadratically with time.
Acceleration is the derivative of velocity, which in free fall is simply -g.
The impact of altitude on the acceleration due to gravity and its variation with height.
The kinematic equations' applicability primarily near the Earth's surface.
The concept of free fall and how it relates to the acceleration due to gravity.
The linear increase in speed of a falling object and the quadratic change in position.
The importance of the constant acceleration assumption in using kinematic equations for motion analysis.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: