Order and Degree of Differential Equations | Differential Equations #order #degree #differential
TLDRThis educational video introduces viewers to Unit 3, focusing on Differential Equations. It begins with a clear definition of differential equations, highlighting their importance in mathematics by explaining how they involve derivatives of dependent variables with respect to one or more independent variables. The video then delves into explaining the 'order' and 'degree' of differential equations, emphasizing that the order is determined by the highest derivative, while the degree is defined by the power of the highest derivative, provided the equation is free from fractions and radicals. Through several examples, the instructor demonstrates how to calculate the order and degree of given differential equations, offering a comprehensive guide for students to understand and solve problems related to differential equations.
Takeaways
- 📚 The lesson is about learning differential equations, specifically focusing on higher order derivatives and their properties.
- 🔍 The importance of understanding the order and degree of a differential equation is emphasized for solving complex problems.
- 🌟 The definition of a differential equation is discussed, highlighting the need to be free from fractions and radicals for higher order derivatives.
- 📈 The concept of the highest order derivative and how to determine its order and degree is explained with examples.
- 🤔 The process of finding the highest derivative involves taking the derivative repeatedly until no more derivatives can be taken.
- 📊 The solution to a given differential equation is demonstrated, showing the steps to find the order and degree of the highest derivative.
- 👓 It is clarified that the degree of the highest derivative is the power of the derivative, which must be determined to solve the equation.
- 🧩 The role of coefficients and radicals in determining the order and degree of a differential equation is discussed, noting their absence in certain cases.
- 🔢 The method for solving higher order differential equations, including taking squares of both sides and simplifying, is outlined.
- 🎓 The script provides a comprehensive guide on solving second order differential equations with constant coefficients, free from fractions and radicals.
- 🚀 The application of these concepts is shown through examples, reinforcing the understanding of differential equations and their solutions.
Q & A
What is the main topic of the script?
-The main topic of the script is about learning differential equations, including understanding their definitions, orders, and degrees, as well as how to solve them.
What is the first definition mentioned in the script related to differential equations?
-The first definition mentioned is the differential equation itself, which is an equation that relates a function and its derivatives.
What does the script mean by 'equation is free from fraction and radicals'?
-The script refers to the condition where the differential equation does not contain any fractions or radicals in its terms, which simplifies the process of finding the order and degree of the differential equation.
What is the highest order derivative mentioned in the script?
-The highest order derivative mentioned in the script is the second-order derivative, denoted as d^2y/dx^2.
How does the script suggest finding the order and degree of a differential equation?
-The script suggests that to find the order and degree of a differential equation, one must first ensure that the equation is free from fractions and radicals, then identify the highest order derivative present in the equation, which will determine the order, and its power, which will determine the degree.
What is the solution process for a second-order differential equation as described in the script?
-The script outlines a solution process that involves taking squares of both sides of the equation, dealing with the resulting terms, and simplifying to find the solution, which in the given example is expressed as the square root of a certain expression involving the second derivative.
What is the role of the highest order derivative in solving differential equations?
-The highest order derivative plays a crucial role in determining the order of the differential equation, which is necessary for understanding the structure of the equation and for applying the correct methods to solve it.
How does the script address the concept of 'degree' in differential equations?
-The script explains that the degree of a differential equation is related to the power of the highest order derivative. It is used to classify the equation and is crucial in the process of solving it.
What is the significance of the term 'dydekop.org' mentioned in the script?
-The term 'dydekop.org' appears to be a placeholder or a typo in the script, likely representing a variable or a constant term in the differential equation. The exact significance is not clear from the context provided.
What is the final example given in the script to illustrate the solution of a differential equation?
-The final example given in the script is a second-order differential equation, where the solution process involves taking the square root of a certain expression derived from the equation, which results in a simple form of the solution.
How does the script conclude in terms of solving differential equations?
-The script concludes by emphasizing the importance of obtaining the highest order derivative and its power to solve differential equations effectively, and by providing a general approach to solving such equations.
Outlines
📚 Introduction to Differential Equations
This paragraph introduces the concept of differential equations, specifically focusing on the third order linear differential equation with constant coefficients. It discusses the importance of understanding the order and degree of the differential equation, as well as the conditions for it to be considered well-posed. The paragraph emphasizes the need to ensure that the differential equation is free from fractions and radicals to facilitate the process of finding the highest order derivative and its degree.
🔢 Solving Second Order Differential Equations
The second paragraph delves into solving second order differential equations by taking squares on both sides and applying the given differential equation to find the highest order derivative and its power. It explains the process of squaring both sides of the equation and how to handle the left and right-hand sides to arrive at the solution. The paragraph also touches on the concept of the highest order derivative and its power in relation to the degree of the differential equation.
🧮 Techniques for Solving Third Order Equations
This paragraph discusses the methodology for solving third order differential equations, including the use of cubes on both sides to eliminate power fractions. It explains how to deal with the left-hand side involving the square of the second derivative and the right-hand side involving the cube of the second derivative. The paragraph also covers how to write the differential equation in terms of the highest order derivative and its power, and how to solve it by considering the degree and order of the given differential equation.
Mindmap
Keywords
💡Differential Equation
💡Order of Differential
💡Degree of Differential
💡Derivative
💡Fractions and Radicals
💡Highest Order Derivative
💡Domain
💡Solving Differential Equations
💡Variables
💡Order and Degree
Highlights
The introduction of the concept of learning about units, specifically Unit Number Three, which is about differential equations.
Explaining the first of all definitions, which is the definition of a differential equation.
Discussing the importance of understanding the order and degree of a differential equation.
The definition of a first-order differential equation and its relation to the highest order derivative.
The method to find the order and degree of a given differential equation.
The requirement for a differential equation to be free from fractions and radicals to find the highest order derivative.
The process of solving higher-order differential equations by reducing them to first-order systems.
The explanation of how to solve a second-order differential equation using the square of both sides method.
The solution to the given differential equation, involving the square root of a sum of terms.
The concept of a differential coefficient and how it relates to the order and degree of a differential equation.
The method to find the highest order derivative when the differential coefficient is not present in the denominator.
The explanation of the solution to a given differential equation, involving the power of a differential expression.
The process of finding the highest order derivative and its power for a given differential equation.
The solution to a specific example involving the power of the highest order derivative.
The method to solve a differential equation by taking the square root of both sides and dealing with radicals.
The final solution to a complex differential equation, demonstrating the application of various mathematical techniques.
The conclusion of the video, summarizing the process of obtaining the degree and order of a given differential equation.
Transcripts
Browse More Related Video
Calculus - Order and Degree of a Differential Equation | Don't Memorise
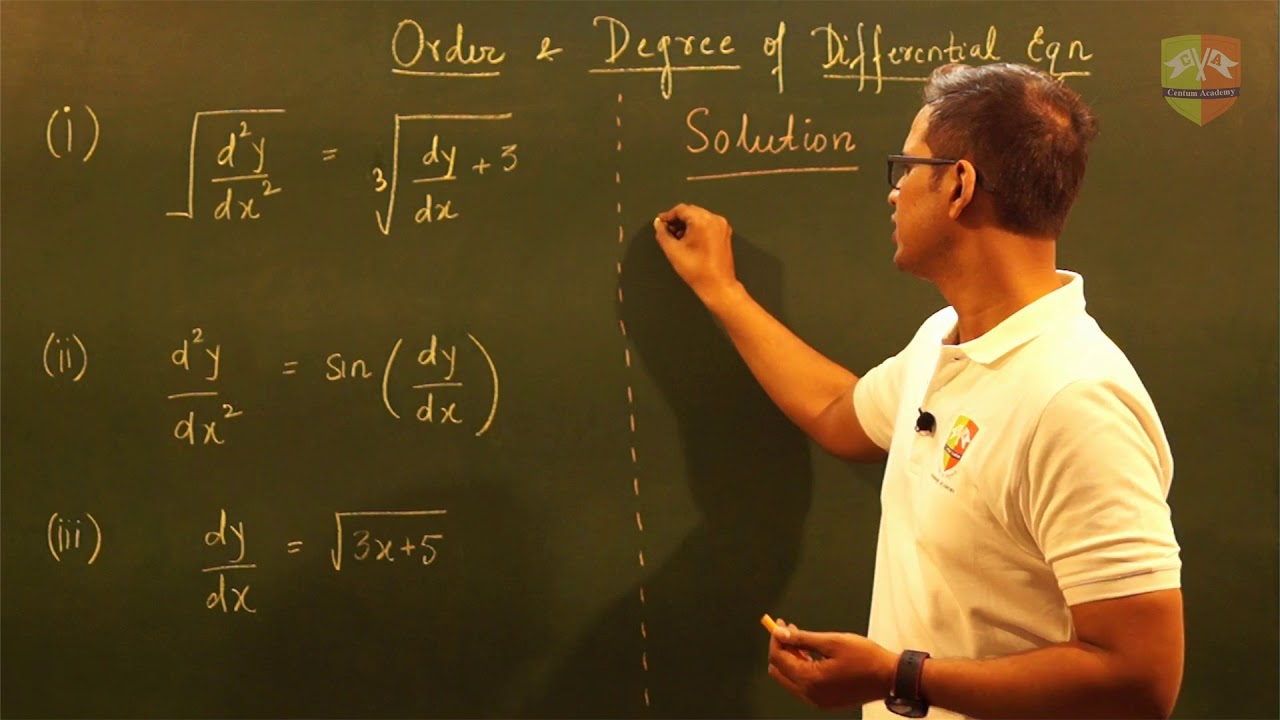
Differential Equations - Introduction - Part 1
Converting a Higher Order ODE Into a System of First Order ODEs
The Theory of 2nd Order ODEs // Existence & Uniqueness, Superposition, & Linear Independence
Initial Value Problem
Differential Equations BC Calculus
5.0 / 5 (0 votes)
Thanks for rating: