Pre-Calculus - Find the linear regression line using the TI-83/84 calculator (2)

MySecretMathTutor
7 Oct 201105:25
EducationalLearning
32 Likes 10 Comments

TLDRThis tutorial guides viewers through the process of inputting and visualizing data using a calculator's scatter plot feature. The instructor meticulously demonstrates how to set up a scatter plot, adjust the viewing window for optimal data display, and then proceed to fit a linear regression line through the data points for analysis. Emphasizing the practical application, the tutorial also explores how to store the regression equation in the calculator for future predictions. By inputting a hypothetical value, the instructor showcases how to use the stored linear model to predict outcomes not present in the original dataset, illustrating the calculator's capability to serve as a valuable tool for mathematical analysis and prediction.

Takeaways
  • 📝 All data is now stored in the calculator, ready for analysis and visualization.
  • 📈 Setting up a scatter plot involves going to the 'Second stat plot' and ensuring 'Plot 1' is selected.
  • 🔍 The scatter plot configuration includes turning it on, setting it to pull data from list one and list two, and choosing 'Mark' as boxes.
  • 🛠 Adjusting the window settings is crucial to display all data properly, with X values between -10 and 60, and Y values between 0 and 5.
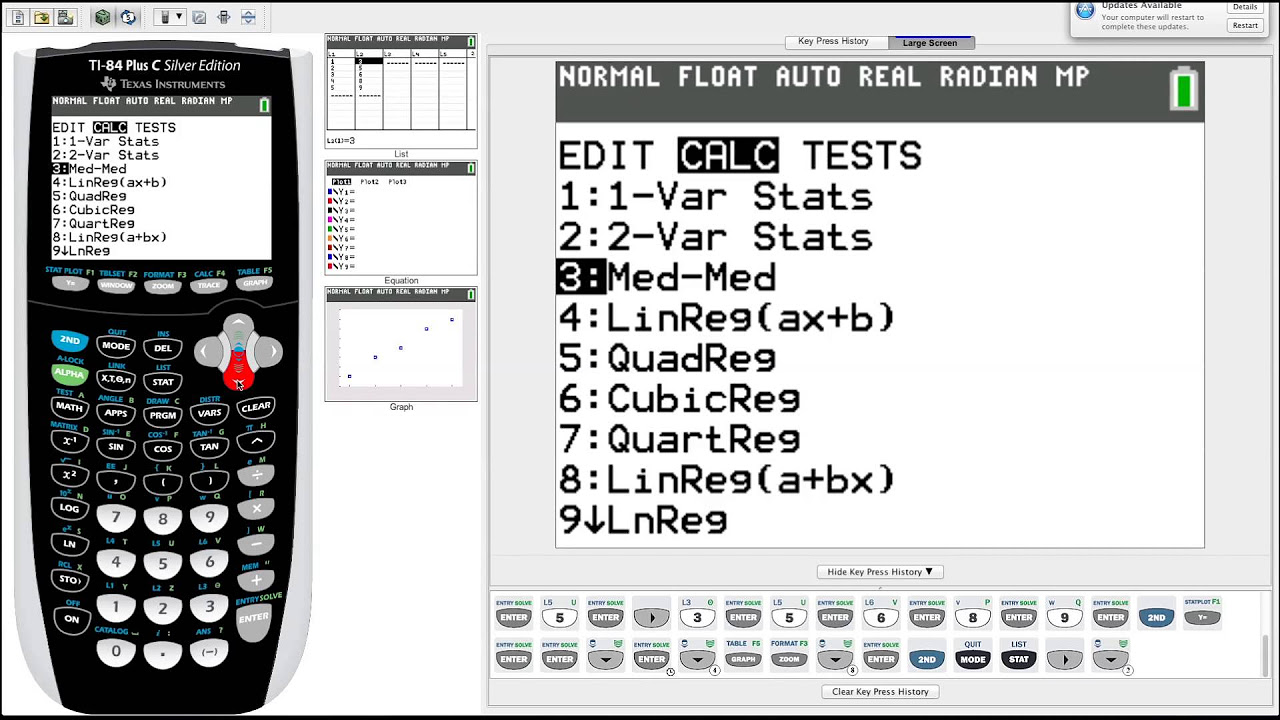
  • 📉 To form a best fit line through the data points, navigate to the 'stat' option, then 'calc', and select 'linear regression'.
  • 💾 Data for linear regression is specified to come from list one and list two, entered using the 'second' button plus the number of the list.
  • ✏️ Storing the linear regression line in the calculator is done by pressing the 'variables' button, selecting Y variables, and choosing 'y1'.
  • 📅 The calculator outputs the slope, Y intercept, and correlation coefficient for the regression line, indicating the fit quality.
  • 📖 Accessing the stored equation under 'y1' allows for viewing both the data and the best fit line on the graph.
  • 📊 Making predictions for future values not in the data set is possible by using the stored linear regression model and entering a new X value.
Q & A

  • How can you store data in a calculator for plotting?

    -The data is stored inside the calculator, likely in lists, to be used for plotting, such as for creating a scatter plot.

  • What are the steps to set up a scatter plot on the calculator?

    -To set up a scatter plot, go to 'Second stat plot', select 'plot one', turn it on, ensure it's set to scatter plot, and specify the data sources from list one and list two.

  • How do you adjust the viewing window for a scatter plot on the calculator?

    -Adjust the viewing window by specifying the range of x and y values, such as x values between -10 and 60, and y values between 0 and 5.

  • What is the purpose of creating a best fit line through data points on a scatter plot?

    -Creating a best fit line through data points on a scatter plot helps in understanding the relationship between the variables and making predictions based on the data.

  • How do you perform a linear regression on the calculator using stored data?

    -Perform a linear regression by going to the 'stat' option, selecting 'calc', choosing linear regression (number 4), and specifying the data stored in list one and list two.

  • How can you store the linear regression line equation in the calculator?

    -Store the linear regression line equation by specifying to store the line in y1, using the 'variables' button, selecting 'Y variables' and choosing 'function' for y1.

  • What information does the calculator provide after performing linear regression?

    -After performing linear regression, the calculator provides the coefficients of the line, such as the slope and the Y-intercept, and the correlation coefficient to indicate the fit of the line.

  • How can you use the calculator to make predictions using the best fit line?

    -To make predictions, use the stored linear model to input a value for x (e.g., 75), and the calculator will output the predicted y value based on the linear regression line.

  • What advantage does storing the linear regression function in the calculator provide?

    -Storing the linear regression function in the calculator allows for easy access to the model for making predictions about future values not present in the initial data.

  • Where can viewers find more instructional videos according to the transcript?

    -Viewers interested in more instructional videos can visit mysecretmathtutor.com as mentioned in the transcript.

Outlines
00:00
📊 Setting Up and Interpreting Scatter Plots on a Calculator

The video begins with a tutorial on how to store data within a calculator and proceed to set up a scatter plot. It guides viewers through enabling a scatter plot feature, ensuring it pulls data from two specified lists, and customizing the plot with a specific marker. Following this, the tutorial covers adjusting the window settings to adequately display the data with appropriate x and y values. It transitions into forming a best-fit line through the data points by utilizing the calculator's statistical functions, specifically focusing on linear regression. The process involves selecting the linear regression option, specifying the data lists to be used, and instructing the calculator to store the regression line equation. The tutorial concludes this section by showcasing how the calculator successfully calculates and displays the coefficients, including the slope and y-intercept, along with the correlation coefficient, thereby indicating the fit of the line. It emphasizes the utility of storing the equation for future reference and predictions.

05:01
📈 Making Predictions with Linear Regression

This section demonstrates how to use the calculator's stored linear regression line to make predictions for values not included in the original dataset. It walks through the process of invoking the stored regression equation and inputting a hypothetical value (in this case, x=75) to predict its corresponding y-value based on the regression line. The predicted outcome is shared, and the tutorial underscores the predictive power of linear regression models stored in calculators. The video wraps up by encouraging viewers to engage with more educational content on the provided website, highlighting the resource as a platform for further learning in mathematics.

Mindmap
Keywords
💡Calculator
In the context of the script, a calculator refers to a graphing calculator, a handheld device capable of plotting graphs, solving equations, and performing statistical functions. The video guides viewers on using a graphing calculator to store data, set up scatter plots, and perform linear regression. The calculator stores data in lists, plots data points, and computes the best fit line, illustrating its functionality in data analysis and mathematical modeling.
💡Scatter Plot
A scatter plot is a type of graph used to represent the relationship between two variables, showing data points plotted on a Cartesian coordinate system. In the script, setting up a scatter plot is a primary step for visualizing the data stored in the calculator, allowing the viewer to see the distribution of data points and prepare for further analysis like regression.
💡Data
Data in this context refers to the numerical or categorical information stored in the calculator's lists. The script details how to manipulate and visualize this data using the calculator, like plotting it on a scatter plot or using it in a linear regression analysis. Data is fundamental for the calculator's functions discussed, such as creating plots and statistical modeling.
💡Linear Regression
Linear regression is a statistical method used to model the relationship between a dependent variable and one or more independent variables. The script explains how to perform linear regression on the calculator, using stored data to calculate and display the regression line, which predicts the relationship between the variables.
💡List
In the context of the video script, a list refers to a data structure in the calculator where numerical data are stored. The script mentions storing data in 'list one' and 'list two,' indicating these as sources for plotting and analysis, like in scatter plots and regression calculations.
💡Regression Line
A regression line is the output of a linear regression analysis, representing the best fit straight line through a set of data points. In the video, the calculator computes this line to show the linear relationship between the data in lists, providing insights into trends and patterns.
💡Coefficients
Coefficients in linear regression, such as the slope and Y intercept, are the values that multiply the predictor variables and the constant term in the equation. The video discusses these as part of the output from the calculator's linear regression function, indicating the nature of the linear relationship modeled.
💡Correlation Coefficient
The correlation coefficient is a statistical measure that calculates the strength and direction of a linear relationship between two variables. In the script, it's mentioned as part of the linear regression output, helping to determine how well the regression line represents the data points.
💡Prediction
Prediction in this context refers to estimating future values based on the linear regression model. The script shows how to use the calculator to predict values for unmeasured points, like an x-value of 75, demonstrating the practical application of the regression analysis for forecasting.
💡Function
The term 'function' here refers to mathematical functions stored in the calculator, specifically in context to storing the regression equation as 'y1'. The video illustrates how to use these stored functions to evaluate new data points and integrate them into further analysis or predictions.
Highlights

Data storage in calculator for scatter plot setup.

Initiating scatter plot using 'Second stat plot' with plot one selected.

Turning on scatter plot and setting data source to list one and list two.

Customizing the graph window to display all data points.

Graphing the data to visualize the scatter plot.

Navigating to 'stat' for linear regression line calculation.

Selecting linear regression option in calculator's 'calc' menu.

Specifying data lists for linear regression analysis.

Storing the regression line in calculator's 'y1'.

Displaying the coefficients of the regression line, including slope and Y-intercept.

Accessing the stored regression equation in 'y1' for graphing.

Graph shows both data points and the best fit line.

Using the stored linear model for future value predictions.

Demonstrating prediction of value for x=75 using the regression line.

Conclusion with the predicted output and invitation to visit educational website.

Transcripts

Browse More Related Video

Residual Plot on TI-84 Plus

Least Squares Regression Line on the TI83 TI84 Calculator

Quadratic Regression TI 84

How to do Linear Regression on the TI84 Plus CE

TI-84 Plus Graphing Calculator Guide: Statistics

How to calculate linear regression using least square method

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Data AnalysisLinear RegressionCalculator TutorialPredictive ModelingStatistical LearningMath EducationScatter PlotsCorrelation CoefficientVideo TutorialData Visualization