8.01x - Lect 24 - Rolling Motion, Gyroscopes, VERY NON-INTUITIVE
TLDRThe transcript discusses the principles of torque, angular momentum, and their effects on rolling objects, specifically cylinders and spheres, as they roll down a slope. It delves into the concept of pure roll, where an object rolls without slipping or skidding, and the conditions required for this to occur. The script also explores the dynamics of spinning objects like gyroscopes and their nonintuitive behavior when torque is applied, leading to precession. The lecture includes thought-provoking demonstrations and experiments that challenge intuition and highlight the importance of angular momentum in the stability of spinning objects, with applications in inertial guidance systems.
Takeaways
- 🌀 The concept of pure roll is when an object rolls down a slope without skidding or slipping, maintaining the same velocity at the center and the circumference.
- 📐 When an object undergoes pure roll, the acceleration of the center of mass is given by a = (2/3)g*sin(beta) for a solid cylinder, where 'g' is the acceleration due to gravity, and 'beta' is the slope angle.
- 🏎️ In a race between two solid cylinders with the same mass and length but different radii, neither will win as the acceleration and thus the speed depend only on the geometry of pure roll, not on mass or radius.
- 🔄 For a hollow cylinder, the acceleration is given by a = (1/2)g*sin(beta), which is less than that of a solid cylinder, making the hollow cylinder the loser in a race.
- 🏍 The moment of inertia about the center of mass for a solid cylinder is (1/2)MR^2, which affects the acceleration and speed during pure roll.
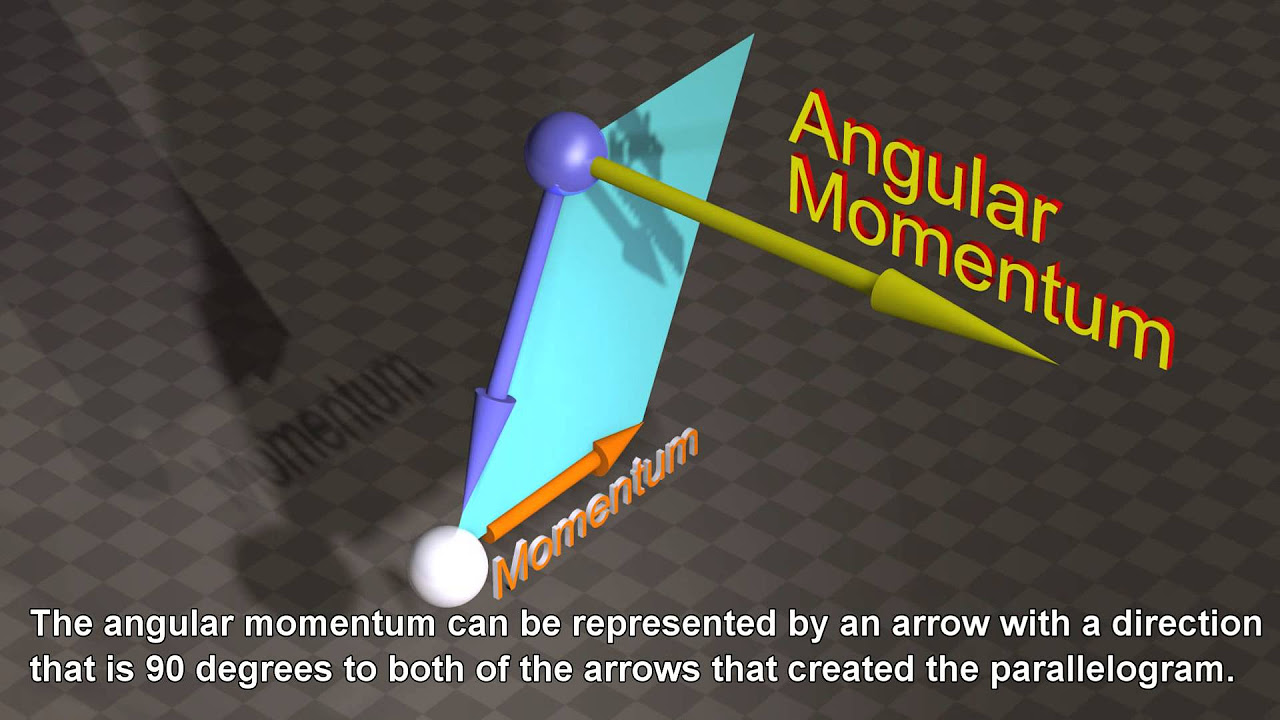
- 🤹♂️ Gyroscopes and spinning objects exhibit nonintuitive behavior when torque is applied, leading to precession, where the spin angular momentum vector moves in the direction of the applied torque.
- 🚀 In outer space, a spinning wheel will maintain its angular momentum and orientation unless acted upon by an external torque, demonstrating the conservation of angular momentum.
- 🎢 When a torque is applied to a spinning wheel, the wheel precesses, and the angular momentum vector tilts or changes direction to align with the torque.
- 🪀 Toy gyroscopes demonstrate the same principles as larger, more complex systems, showing that the principles of physics apply universally regardless of scale.
- 🛠️ Spin angular momentum has a stabilizing effect on objects, which is the principle behind inertial guidance systems used in aviation and space travel.
- 💡 The precession frequency is determined by the ratio of the applied torque to the spin angular momentum, and it can be increased by increasing the torque without changing the mass or radius of the spinning object.
Q & A
What is the condition for pure roll as described in the transcript?
-The condition for pure roll is when the velocity of the center of mass (point Q) and the velocity of the circumference are the same, meaning there is no slipping or skidding, and the object is rolling without any lateral motion.
How does the acceleration of a rolling object without friction depend on its radius?
-If there is no friction, the acceleration of a rolling object depends solely on gravity and the sine of the slope angle (beta), and it is independent of the object's radius, mass, and length when the object is solid.
What happens when two solid cylinders with the same mass and different radii roll down a slope?
-When two solid cylinders with the same mass and different radii roll down a slope, neither one will win the race as their accelerations will be the same, resulting in them reaching the bottom simultaneously.
What is the relationship between the moment of inertia and the acceleration of a hollow cylinder rolling down a slope?
-For a hollow cylinder, the moment of inertia about the center of mass is closer to MR squared, where M is the mass and R is the radius. This results in a lower acceleration compared to a solid cylinder, making the hollow cylinder lose in a race against a solid cylinder with the same mass, radius, and length.
How does the angular momentum of a spinning object behave when a torque is applied to it?
-When a torque is applied to a spinning object, the angular momentum vector will move or tilt in the direction of the applied torque. This behavior is known as precession and is a nonintuitive aspect of spinning objects.
What is the role of spin angular momentum in stabilizing objects?
-Spin angular momentum has the property of stabilizing objects. When an object like a bicycle wheel, a quarter, or a top is spinning, it becomes more stable and less likely to fall over due to its angular momentum.
How does the precession frequency of a spinning object relate to the applied torque and its spin angular momentum?
-The precession frequency of a spinning object is directly proportional to the applied torque and inversely proportional to the spin angular momentum. Increasing the torque increases the precession frequency, while increasing the spin angular momentum decreases the precession frequency.
What is inertial guidance and how does it use gyroscopes?
-Inertial guidance is a navigation technique that uses gyroscopes to maintain a vehicle's desired course. The gyroscopes, which are spinning wheels mounted in a way that prevents torque on their axis, provide a stable reference direction. Any change in the vehicle's direction causes the gyroscope's housing to rotate, and this rotation is fed back to the automatic pilot to keep the vehicle on course.
How does the script demonstrate the concept of torque and angular momentum in real-world scenarios?
-The script demonstrates the concept of torque and angular momentum through various experiments and real-world examples, such as rolling cylinders down a slope, spinning wheels in outer space, and the use of gyroscopes in inertial guidance systems. These examples show how torque affects the angular momentum of objects and how angular momentum can stabilize objects or cause them to precess.
What is the significance of the moment of inertia in the analysis of rolling objects?
-The moment of inertia is crucial in determining the acceleration of rolling objects. It appears in the equations that relate the torque applied to an object, its angular acceleration, and its linear acceleration. For solid and hollow cylinders, the moment of inertia affects their respective accelerations differently, leading to different outcomes in races down a slope.
How does the script use the concept of torque to explain the behavior of spinning tops and gyroscopes?
-The script explains that when a torque is applied to a spinning top or gyroscope, the spin angular momentum of the object will start to precess or tilt in the direction of the applied torque. This behavior, known as precession, is a fundamental concept in understanding how gyroscopes work and is used in inertial guidance systems to maintain a stable direction of travel.
Outlines
🌀 Introduction to Torque and Rolling Objects
The paragraph introduces the concept of torque and its application to rolling objects, specifically cylinders and spheres, down a slope. It discusses the conditions for pure roll, where the object does not skid or slip, and the relationship between the velocity of the center point and the circumference. The speaker also poses a question about a race between two cylinders of different radii but the same mass and length, asking which would reach the bottom first and discussing the intuition behind the answer.
📐 Mathematical Analysis of Pure Roll
This paragraph delves into the mathematical aspects of pure roll, explaining the relationship between velocity, acceleration, and angular acceleration. It introduces the torque equation and Newton's second law to derive the acceleration of a rolling cylinder. The speaker also discusses the conditions under which the mass, radius, and length of the cylinders do not affect the outcome of the race, leading to the counterintuitive conclusion that all solid cylinders, regardless of their physical differences, would result in a tie.
🏎️ The Race of Cylinders: Hollow vs Solid
The speaker addresses the case of hollow versus solid cylinders, explaining how the distribution of mass affects the outcome. It is shown that a hollow cylinder will lose a race against a solid cylinder regardless of their masses or radii. The speaker demonstrates this with a physical setup, showing that a heavy brass cylinder and a light aluminum cylinder of the same dimensions reach the bottom at the same time, while a hollow cylinder falls behind.
🚀 Gyroscopes and Nonintuitive Physics
The paragraph introduces gyroscopes and their nonintuitive behavior. The speaker describes a thought experiment in outer space with a spinning bicycle wheel and the effects of applying torque in different scenarios. It explains how the wheel's angular momentum changes in response to the applied torque and how this leads to the wheel tilting or precessing in unexpected ways. The speaker emphasizes the importance of paying close attention to understand these concepts.
🌪 Precession of a Spinning Wheel
This paragraph explains the concept of precession in spinning objects, particularly wheels. The speaker describes how applying torque to a spinning wheel results in the wheel tilting and precessing, with the angular momentum of the wheel moving in the direction of the applied torque. The speaker uses a visual demonstration to show how the wheel's precession is nonintuitive and can be predicted by understanding the relationship between torque and angular momentum.
🎢 The Physics of a Hanging Wheel
The speaker discusses a hanging wheel system, where the wheel is spun and then allowed to precess due to the torque provided by gravity. The paragraph explains how the spin angular momentum of the wheel moves in response to the gravitational torque and how this results in the wheel precessing around its axis. The speaker also addresses the safety and practical considerations of such demonstrations, highlighting the nonintuitive nature of the physics involved.
🛠️ Inertial Guidance Systems and Stabilization
The paragraph discusses the application of spinning objects and their angular momentum in inertial guidance systems, such as those used in airplanes and missiles. It explains how a spinning wheel mounted in a specific way (three-axle-gimbaled gyros) can be used to maintain a stable direction, as the wheel's spin angular momentum remains constant. The speaker also demonstrates how applying torque to a spinning wheel can cause it to precess and change direction, further illustrating the principles behind inertial guidance.
Mindmap
Keywords
💡Torque
💡Angular Momentum
💡Friction
💡Precession
💡Inertia
💡Moment of Inertia
💡Gyroscopes
💡Pure Roll
💡Angular Acceleration
💡Inertial Guidance System
Highlights
The concept of pure roll is introduced, where an object rolls down a slope without skidding or slipping.
The definition of pure roll is given, where the center of mass moves a distance of 2πR in one complete rotation of the object.
The relationship between the velocity of the center of mass and the velocity of the circumference during pure roll is explained.
An experiment is proposed to race two cylinders of different radii but the same mass and length to determine which will reach the bottom first.
The conclusion that neither cylinder will win the race if they are both solid and have the same mass, length, and pure roll conditions is presented.
The moment of inertia for a solid cylinder rotating about its center of mass is derived as 1/2 MR^2.
An equation for acceleration of a rolling object is developed, showing that it depends on the sine of the slope and the moment of inertia.
A hollow cylinder is shown to lose a race against a solid cylinder of any mass, radius, or length due to its higher moment of inertia.
The nonintuitive behavior of spinning objects, such as gyroscopes, is introduced with a demonstration of a bicycle wheel in outer space.
The concept of angular momentum and its relationship with torque is explored, leading to the phenomenon of precession.
A demonstration shows that when a spinning wheel is subjected to torque, it tilts rather than continuing to rotate as one might expect.
The direction of precession is shown to be related to the direction of the applied torque, with a visual demonstration of a spinning wheel tilting in response to torque.
The concept of spin angular momentum stabilizing objects is introduced, with examples such as a spinning bicycle wheel not falling over.
Inertial guidance systems are explained as a practical application of spinning objects with stabilizing effects.
A demonstration of a gyroscope with weights on its axis shows the effect of changing torque on the precession frequency.
The nonintuitive nature of spinning objects and their response to torque is emphasized through various demonstrations and experiments.
A toy gyroscope is used to illustrate the same principles as the larger demonstrations, showing the universality of the phenomena.
The transcript concludes with a humorous demonstration involving a suitcase and a student at an airport, highlighting the unexpected behavior of spinning objects under torque.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: