Decimals to Fractions
TLDRThis informative video script outlines the process of converting decimal numbers into fractions and mixed numbers. It begins with simple examples, like 0.4 and 0.8, and progresses to more complex cases, including repeating decimals. The script emphasizes the importance of finding common denominators and reducing fractions where possible. Various methods are presented, such as breaking down numbers into smaller parts and using long division, allowing viewers to choose the approach that suits them best. The goal is to provide viewers with a comprehensive understanding of decimal-to-fraction conversion, empowering them to tackle such problems with ease and efficiency.
Takeaways
- 📝 To convert a decimal to a fraction, start by writing the decimal number over 1.
- 🔢 Eliminate the decimal point by multiplying both the numerator and denominator by 10, 100, or an appropriate power of 10 depending on the number of decimal places.
- 🧮 After conversion, simplify the resulting fraction by dividing both the numerator and denominator by their greatest common divisor (GCD).
- 📈 For repeating decimals, express the non-repeating part as a fraction and then add the repeating part as a separate fraction with an appropriate denominator.
- 🔄 To convert an improper fraction to a mixed number, separate the whole number from the fractional part and express it as the sum of the whole number and the fraction.
- 🤔 When dealing with complex decimals, like 4.91 repeating, break down the problem into smaller parts and handle each part separately before combining them.
- 📊 For decimals with multiple repeating digits, like 0.39 repeating, divide the numerator and denominator by the product of the repeating digits to simplify the fraction.
- 🌟 Use mental math or long division to find how many times the denominator goes into the numerator when converting improper fractions to mixed numbers.
- 🔧 When faced with large numbers, breaking them down into smaller components can make the process of simplifying fractions more manageable.
- 📝 Practice and repetition are key to mastering the skill of converting decimals to fractions and vice versa.
- 🎓 Understanding the principles of fraction simplification and the manipulation of numerators and denominators is crucial for accurate conversion between decimals and fractions.
Q & A
How does one convert a decimal number into a fraction?
-To convert a decimal number into a fraction, you first write the number over 1 and then multiply both the numerator (top number) and the denominator (bottom number) by 10 for each digit after the decimal point. After that, simplify the resulting fraction by dividing both numbers by their greatest common divisor.
What is the fraction equivalent of the decimal 0.4?
-The decimal 0.4 is equivalent to the fraction 2/5. This is obtained by multiplying both the numerator (0.4) and the denominator (1) by 10, resulting in 4/10, which can then be simplified by dividing both the numerator and the denominator by 2.
How can you convert an improper fraction into a mixed number?
-To convert an improper fraction into a mixed number, you divide the numerator by the denominator. The quotient becomes the whole number part of the mixed number, and the remainder becomes the numerator of the fractional part, with the denominator remaining the same.
What is the process for converting a decimal with multiple digits after the decimal point into a fraction?
-For decimals with multiple digits after the decimal point, you multiply the number by a power of 10 for each digit (e.g., 100 for two digits, 1000 for three digits, etc.). This shifts the decimal point to the right, creating a whole number. Then, you write this number over the corresponding power of 10 as the denominator and simplify the fraction if possible.
How do you simplify the fraction 46/10?
-To simplify the fraction 46/10, you divide both the numerator (46) and the denominator (10) by their greatest common divisor, which is 2 in this case. So, 46 divided by 2 is 23, and 10 divided by 2 is 5. The simplified fraction is 23/5.
What is the mixed number equivalent of the improper fraction 47/5?
-The mixed number equivalent of the improper fraction 47/5 is 9 and 2/5. You get this by dividing the numerator (47) by the denominator (5), which gives you a quotient of 9 and a remainder of 2. The quotient is the whole number part of the mixed number, and the remainder becomes the numerator of the fractional part, with the denominator remaining the same.
How do you convert a repeating decimal into a fraction?
-To convert a repeating decimal into a fraction, you can express the repeating decimal as a series of terms with the repeating pattern subtracted from the original number. This allows you to create an equation with a non-repeating decimal, which can then be converted into a fraction using the usual methods.
What is the fraction equivalent of the repeating decimal 0.36 repeating?
-The repeating decimal 0.36 repeating is equivalent to the fraction 23/61. This is derived by subtracting the repeating part (0.36) from the original number (1.00), which gives 0.64. Then, 0.64 is expressed as a fraction, and the repeating part (23/61) is added back in the form of an infinite series.
How do you convert a decimal with a non-repeating and a repeating part, like 4.91(5), into a fraction?
-To convert a decimal like 4.91(5) into a fraction, you first separate the non-repeating part (4.91) from the repeating part (5). The non-repeating part is converted into a fraction as usual. The repeating part is converted by recognizing that it's a repeating decimal and expressing it as a fraction using the method for converting repeating decimals into fractions. Then, you combine the two fractions.
What is the process for converting a decimal with a repeating pattern involving more than one digit, like 0.(39) repeating, into a fraction?
-For a repeating pattern involving more than one digit, like 0.(39) repeating, you first express the repeating part as a fraction by dividing the repeating digits by 99 (since there are two digits). Then, you subtract this fraction from the non-repeating part of the decimal. The result is an improper fraction, which can be simplified if possible.
How do you convert a decimal with a repeating part that includes a single digit, like 0.8(3) repeating, into a fraction?
-For a decimal with a repeating part that includes a single digit, like 0.8(3) repeating, you express the repeating part as a fraction (1/3 in this case) and add it to the non-repeating part of the decimal (0.8). You then combine these into a single fraction and simplify if possible.
Outlines
📚 Converting Decimals to Fractions - Basic Concepts
This paragraph introduces the process of converting decimal numbers into fractions. It begins with simple examples, such as converting 0.4 and 0.8 into fractions by multiplying the decimal by 10 and simplifying the resulting fraction. The paragraph emphasizes the importance of maintaining the value of the fraction through equivalent multiplication or division of both the numerator and the denominator. It also presents the method of converting an improper fraction into a mixed number, using the example of 4.6, and explains two different approaches: splitting the numerator into sums of smaller numbers and using long division.
🔢 Advanced Decimal to Fraction Conversions
This paragraph delves into more complex examples of converting decimals to fractions, such as 9.4 and 3.45. It explains the process of multiplying the numerator and denominator by powers of 10 to eliminate the decimal point and then simplifying the resulting fraction by dividing by common factors. The paragraph also introduces the concept of breaking down larger numbers into smaller, more manageable parts to simplify the fraction reduction process. Additionally, it presents alternative methods for converting decimals like 0.28 and 0.35 into fractions, highlighting the flexibility and adaptability of the conversion techniques.
🔄 Handling Repeating Decimals in Fraction Form
This paragraph addresses the conversion of repeating decimals into fractions. It provides specific formulas for converting simple repeating decimals, such as 0.1 repeating to 1/9, and then moves on to more complex examples like 0.39 repeating and 0.436 repeating. The paragraph explains the process of separating the non-repeating and repeating parts, converting each into a fraction, and then combining them to form the final mixed number. It also demonstrates how to convert mixed numbers back into improper fractions, using examples like 5 and 3/7.
🔢 Dealing with Complex Repeating Decimals
This paragraph focuses on the conversion of complex repeating decimals into fractions. It explains the process of identifying the repeating pattern, subtracting the repeating part from the original decimal, and converting the non-repeating part into a fraction. The paragraph uses examples like 0.833 repeating and 0.5215 repeating to illustrate the steps, emphasizing the need to be cautious with the shifting numbers in the repeating pattern. It also shows how to combine fractions with different denominators into a single improper fraction.
📈 Mixed Number and Improper Fraction Conversions
The final paragraph of the script wraps up the video by demonstrating the conversion of a mixed number back into an improper fraction. It uses the example of 4 and 151/165 to show how to multiply the whole number by the denominator and add the numerator to form the new numerator of the improper fraction. The paragraph reinforces the concepts learned throughout the video, emphasizing the ability to convert decimal numbers into various forms of fractions, and thanks the viewers for their attention.
Mindmap
Keywords
💡Decimal to Fraction
💡Simplifying Fractions
💡Improper Fractions
💡Mixed Numbers
💡Greatest Common Divisor (GCD)
💡Repeating Decimals
💡Long Division
💡Multiplying by Powers of 10
💡Reducing Fractions
💡Canceling Common Factors
💡Converting Mixed Numbers
Highlights
The process of converting decimal numbers into fractions begins with simple examples and gradually progresses to more complex ones.
To convert 0.4 into a fraction, write it as 4 over 10, then reduce both the numerator and denominator by dividing by their greatest common divisor (GCD), which in this case is 2.
For the decimal 0.8, multiplying both the numerator and denominator by 10 yields 8 over 10, which simplifies to 4 over 5.
When converting 4.6 into a fraction, the process involves multiplying both the numerator and denominator by 10 to eliminate the decimal, resulting in 46 over 10, which simplifies to 23 over 5.
An improper fraction can be converted into a mixed number by separating the numerator into a sum of multiples of the denominator and then expressing it as a whole number and a fraction.
For the decimal 9.4, multiplying both the numerator and denominator by 10 gives 94 over 10, which simplifies to 47 over 5 and further to 9 and 2/5 as a mixed number.
To convert 0.28 into a fraction, multiply the numerator and denominator by 100, resulting in 28 over 100, which simplifies to 7 over 25.
The decimal 0.35 can be converted into a fraction by multiplying both the numerator and denominator by 100, resulting in 35 over 100, which simplifies to 7 over 20.
For the decimal 3.45, multiplying both the numerator and denominator by 100 yields 345 over 100, which simplifies to 69 over 20, and further to 3 and 9/20 as a mixed number.
When dealing with repeating decimals, such as 0.1 repeating, it can be expressed as 1 over 9, and the fraction can be simplified by dividing both the numerator and denominator by their GCD.
For decimals with multiple repeating digits, like 0.39 repeating, the fraction 39 over 99 can be simplified by dividing both the numerator and denominator by their GCD, which is 3.
In the case of a mixed repeating decimal like 4.36 repeating, the non-repeating part is converted into a fraction and then combined with the repeating part to form the final mixed number.
For more complex decimals like 3.15 repeating, the process involves separating the non-repeating and repeating parts, converting them into fractions, and then combining them with a common denominator.
When the repeating part is a single digit, such as in 0.83 repeating, the repeating decimal can be expressed as a sum of a non-repeating part and the repeating part, which are then converted into fractions and combined.
The video provides a comprehensive guide on converting decimals into fractions and mixed numbers, offering multiple methods and strategies to handle different types of decimals.
The process of converting decimals into fractions can be applied to a wide range of decimal numbers, including those with single or multiple repeating digits.
Transcripts
Browse More Related Video

Multiplying and Dividing Fractions | A Complete Guide | Math with Mr. J
Understanding Fractions, Improper Fractions, and Mixed Numbers

How to EASILY Improve Your Mental Maths | 8 Simple Tricks

Math - Decimal Arithmetic

Mental Math Tricks - Addition, Subtraction, Multiplication & Division!
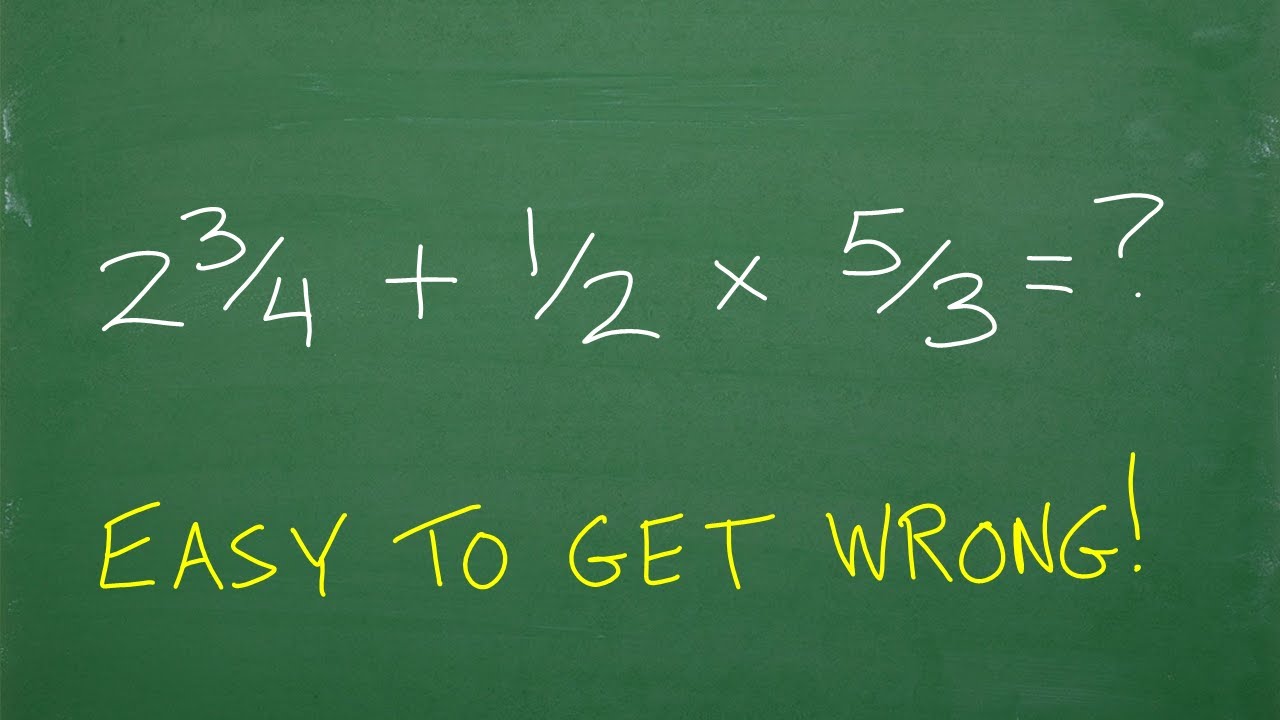
(2 and 3/4) plus 1/2 times 5/3 = ? What’s the first thing you should be thinking in this problem?
5.0 / 5 (0 votes)
Thanks for rating: