How to EASILY Improve Your Mental Maths | 8 Simple Tricks
TLDRThe video script offers a comprehensive guide on improving mental math skills, emphasizing the importance of being able to perform calculations without a calculator. The presenter shares various techniques such as dividing larger numbers into smaller parts, converting fractions into decimals, multiplying numbers by breaking them down into tens or hundreds, and estimating square roots. The video also includes tricks for quickly determining divisibility and multiplying by 11, as well as the benefits of knowing square and prime numbers. The content is practical, with a focus on helping viewers enhance their math skills for exams and daily life.
Takeaways
- 🧠 Mental math is a powerful skill that can significantly improve speed and accuracy in math exams without relying on calculators.
- 📝 Being proficient in mental math involves quickly performing basic operations like addition, subtraction, multiplication, and division with high accuracy.
- 📊 Dividing larger numbers into smaller, more manageable parts can simplify complex calculations in the mind.
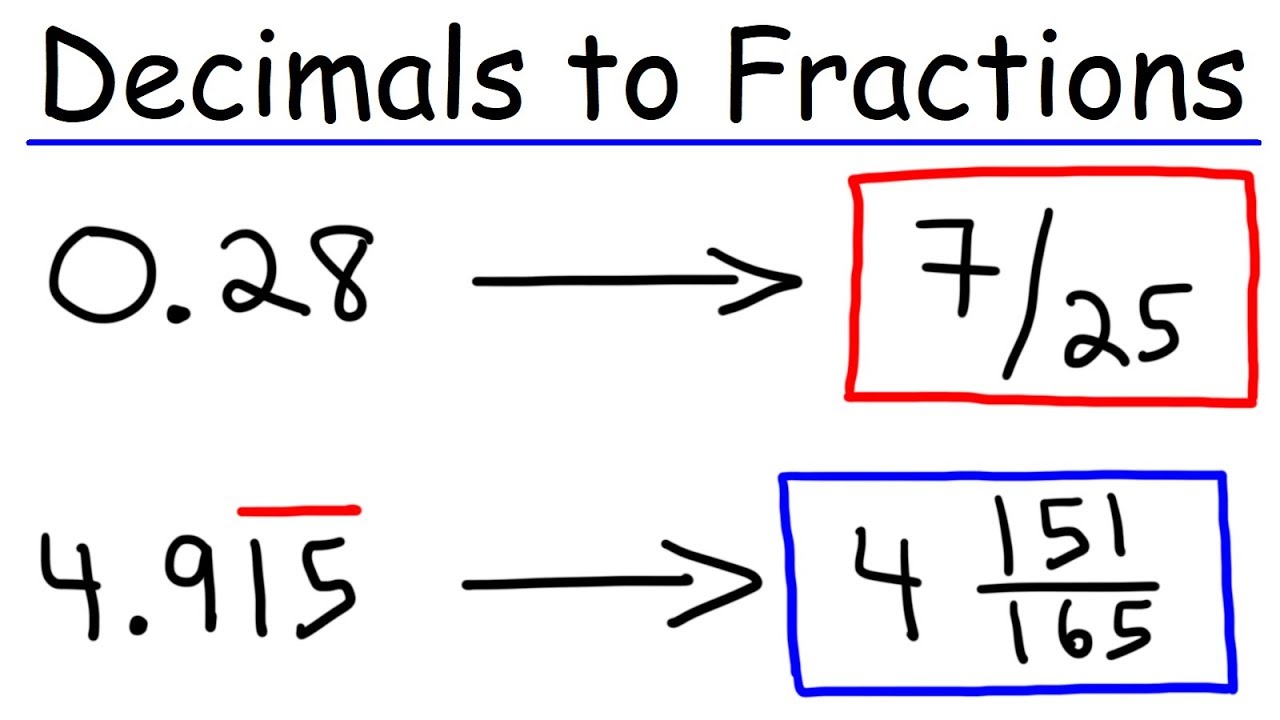
- 🔢 Converting fractions to decimals is a useful skill that can be mastered with practice and knowledge of basic decimal equivalents.
- 🤔 Multiplication can be made easier by breaking numbers into their tens, units, or hundreds and using place value to calculate the result.
- 🌟 Multiplying by five is simplified by doubling the number, multiplying by ten, and then dividing the result by two.
- 📐 Estimating square roots involves familiarity with perfect squares and interpolation between known values.
- 🔄 Divisibility rules, such as for 3 and 11, provide quick mental shortcuts to determine if a number is divisible without actual division.
- 🎯 Memorizing key mathematical values and patterns, like prime and cube numbers, can greatly aid in solving exam problems efficiently.
- 📈 Practice is essential for developing mental math skills; start with paper and pen exercises and gradually build up to mental calculations.
- 📝 Regular quizzes and self-assessment can help track progress and improvement in mental math abilities.
Q & A
What is the main theme of the video transcript?
-The main theme of the video transcript is to teach viewers various techniques and methods to improve their mental math skills, particularly for use in exams and other situations where a calculator may not be available.
What is the first method introduced in the video for mental math?
-The first method introduced in the video is dividing smaller numbers into bigger numbers. This involves breaking down larger numbers into more manageable parts to make mental calculations easier.
How does the video suggest converting fractions into decimals?
-The video suggests memorizing certain key fractions to decimals conversions, such as a half (0.5), a third (0.3 recurring), a fourth (0.25), and a fifth (0.2), and then using these as a basis to quickly convert other fractions into decimals by multiplying the given fraction by the appropriate decimal value.
What is the technique for multiplying two or three-digit numbers by a single digit?
-The technique involves breaking down the larger number into its tens, units, or hundreds (if applicable), multiplying each part by the single digit, and then adding the results together to get the final product.
How does the video explain multiplying by five?
-The video explains that multiplying by five is the same as multiplying by ten and then halving the result. This simplifies the process, as it involves two easy operations regardless of the size of the number being multiplied.
What is the importance of estimating square roots according to the video?
-Estimating square roots is important as it is a skill required in the GCSE math specification. Being able to quickly estimate square roots can save time in exams and provide a good approximation when exact values are not necessary.
How can you check if a number is divisible by three?
-To check if a number is divisible by three, you add up its digits and see if the sum is divisible by three. If the sum is divisible by three, then the original number is also divisible by three.
What is the trick for multiplying a number by 11?
-The trick for multiplying a number by 11 involves splitting the number into its tens and units (or hundreds if applicable), adding these two parts together, and placing the sum between the original tens and units (or hundreds and tens) to get the final product.
What advice does the video give for improving mental math skills in general?
-The video advises becoming familiar with square numbers, prime numbers, and cube numbers up to a certain limit (e.g., 216). Recognizing these numbers can save valuable time in exams and potentially make the difference in one's grade.
How does the video suggest practicing and improving mental math?
-The video suggests practicing mental math techniques on paper first until one becomes comfortable with the methods, and then gradually building up to doing calculations mentally. It also recommends practicing with various difficulty levels of problems and taking quizzes to test one's improvement.
Outlines
🧠 Mental Math Mastery: Introduction and Benefits
This paragraph introduces the concept of mental math and its significance in exams and daily life. It emphasizes the ability to perform calculations quickly and accurately without a calculator. The speaker, a math tutor and university student, shares personal methods for improving mental math skills. A baseline knowledge test is proposed to assess the audience's current mental math abilities, with the intention of comparing results to a final quiz after learning the techniques presented in the video.
📝 Breaking Down Calculations: Dividing and Converting Fractions
The speaker discusses strategies for mental division, such as breaking larger numbers into smaller, more manageable parts. Examples are provided to illustrate how to divide numbers like 424 by 4 and 1344 by 12. The paragraph also covers converting fractions into decimals, offering a method for quick mental conversion and providing examples with fractions like 3/15 and 308/3. The speaker emphasizes the importance of memorizing basic decimal equivalents of fractions and practicing these techniques on paper before attempting them mentally.
🤗 Multiplication Techniques: Estimating and Memorizing
This section focuses on multiplying two or three-digit numbers by a single digit, breaking down the process into manageable steps. The speaker explains how to multiply numbers like 73 by 4 and 162 by 7, emphasizing the importance of practice and memory. A trick for multiplying by five is introduced, which involves doubling the number and then halving the result. The speaker also touches on estimating square roots, a skill required in GCSE math, and provides tips for becoming familiar with square and cube numbers to save time during exams.
Mindmap
Keywords
💡Mental Math
💡Baseline Knowledge Test
💡Dividing Smaller Numbers
💡Fractions to Decimals
💡Multiplying Digits
💡Estimating Square Roots
💡Divisibility Rules
💡Prime Numbers
💡Cube Numbers
💡Practice
💡Exam Performance
Highlights
Mental maths is a powerful skill that can save time and increase accuracy in exams without the use of calculators.
Being good at mental maths involves computing simple calculations like addition, subtraction, multiplication, and division quickly and accurately.
Dividing smaller numbers into bigger ones is a useful technique for real-life applications, such as splitting bills.
Breaking down larger numbers into smaller, manageable parts can simplify mental calculations.
Converting fractions into decimals is a valuable skill that can be used for quick calculations.
Memorizing decimal equivalents of fractions (e.g., a half is 0.5, a third is 0.3 recurring) aids in quick mental math.
Multiplying two or three-digit numbers by a single digit can be done by breaking down the larger number into its tens, units, or hundreds.
Multiplying by five is simplified by doubling the number, then halving the result.
Estimating square roots is a skill required in certain math specifications, like GCSE, and can be improved by knowing square numbers up to 144.
To estimate a square root, find the nearest perfect squares and determine where the number lies between them.
Divisibility rules, such as for 3 or 11, are useful tricks to quickly determine if a number is divisible without calculation.
The trick for multiplying by 11 involves splitting the number and adding the digits in the middle, with carrying over if the sum is greater than 10.
Familiarity with square numbers, prime numbers, and cube numbers up to 216 can provide valuable shortcuts in exams.
Practicing mental math techniques on paper before doing them in one's head can build confidence and skill.
Learning and applying these mental math tips can lead to significant improvements in speed and accuracy.
The video aims to help viewers improve their mental math skills and potentially save their grades in exams.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: