Mental Math Tricks - Addition, Subtraction, Multiplication & Division!
TLDRThe video script offers a comprehensive guide on mental math techniques for quick calculations. It begins with simple addition, suggesting breaking numbers into tens and ones for easier summation, and demonstrates this with examples involving two-digit numbers. The script then progresses to more complex examples, including three-digit numbers, and emphasizes the importance of carrying over numbers when necessary. It also covers subtraction, using a similar breakdown method and applying negative signs where needed. The guide then shifts to multiplication, explaining the concept of repeated addition and using multiplication tables up to twelve for quick results. It provides strategies for multiplying larger numbers by thinking in terms of money or using the distributive property. The script concludes with division, illustrating how to mentally divide numbers by breaking them into smaller, divisible parts and confirming answers with long division. The video is a valuable resource for anyone looking to improve their mental math skills.
Takeaways
- 🧮 **Breaking Down Numbers**: Mental math involves breaking down numbers into smaller, more manageable parts for easier addition.
- 📝 **Straightforward Addition**: Adding numbers like 30 and 50 is straightforward, and then combining the units (4+8=12) to get the final sum (e.g., 92).
- 🔢 **Adding Larger Numbers**: For three-digit numbers, add corresponding place values (hundreds, tens, and units) separately and then combine them.
- 🤔 **Subtraction Technique**: Apply the same breakdown technique to subtraction, ensuring to apply negative signs where appropriate.
- 📉 **Confirming with Long Division**: Use long division to confirm your mental math results, especially for more complex operations.
- 💡 **Multiplication as Repeated Addition**: Understand that multiplication is a form of repeated addition, which simplifies the mental calculation process.
- 💵 **Money Analogy**: Use the concept of money to visualize multiplication problems, especially when dealing with currency denominations.
- 📊 **Distributive Property**: Employ the distributive property to simplify multiplication by breaking down numbers into tens and ones, and then multiplying.
- 🔧 **Division by Multiples**: When dividing by a multiple, break down the number into parts that are easily divisible by the given number.
- 🔠 **Division for Non-Multiples**: For numbers not divisible by the divisor, break them into smaller components that are divisible and then sum the results.
- ✅ **Confirm with Calculator**: Always check your mental math with a calculator to ensure accuracy and reinforce your learning.
Q & A
What mental math technique is suggested for adding two numbers in your head?
-The technique involves breaking down the numbers into their constituent parts, such as tens and ones, and then adding those parts separately to get the final result.
How would you add 69 and 45 using the suggested mental math technique?
-You would break down 69 into 60 and 9, and 45 into 40 and 5. Then add the 60s and 40s to get 100, and the 9s and 5s to get 14, resulting in a total of 114.
What is the process for adding three-digit numbers mentally as described in the script?
-First, add the hundreds place of the numbers, then the tens, and finally the ones. Combine the results step by step, carrying over as necessary.
How can you confirm the mental math result using traditional methods?
-You can confirm the result by using the standard addition or subtraction method, which involves carrying over numbers and aligning the digits properly.
What is the mental math technique for subtracting two numbers?
-Similar to addition, you break down the numbers and subtract the corresponding parts. If necessary, apply a negative sign to the subtrahend and proceed with the subtraction as you would with addition.
How do you mentally multiply two numbers using the script's method?
-You can use the method of repeated addition, where you add the first number a number of times equal to the second number. Alternatively, you can think in terms of money or use the distributive property to simplify the calculation.
What is the mental math trick for multiplying numbers that are close to a round figure like 50 or 100?
-You can rewrite the number as the nearest round figure minus a small number (e.g., 49 as 50 - 1) and then use the distributive property to multiply by the round figure and the subtracted number separately.
How can you mentally divide a number by 2?
-Divide the first digit(s) by 2 and then bring down the next digit to form a new number, dividing it by 2 as well, until you've processed all digits.
What is a simple division trick for dividing by a number that has multiples within the dividend?
-Break down the dividend into smaller numbers that are divisible by the divisor. Then divide each part separately and sum the results to get the final answer.
How do you mentally divide a number by a one-digit number if the number is not easily divisible?
-Break down the number into parts that are divisible by the one-digit number, divide each part, and then sum the quotients to get the final result.
What is the final answer when you divide 168 by 6 using the mental math technique?
-You would break down 168 into 120 and 48, divide each by 6 to get 20 and 8 respectively, and then add those results to get a final answer of 28.
Outlines
🧮 Mental Math Techniques for Addition
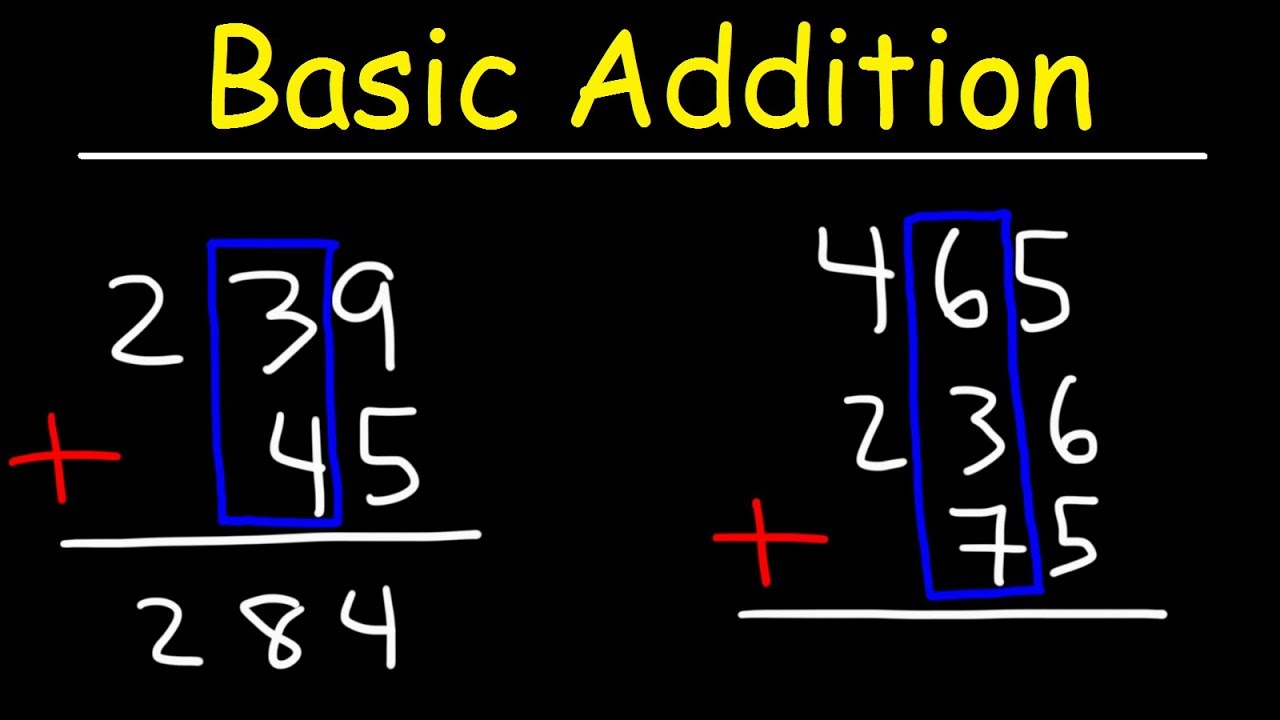
This paragraph introduces mental math techniques for addition. It explains how to break down numbers into smaller, more manageable parts to perform addition quickly. For instance, adding 34 and 58 is done by first adding the tens (30 and 50) and then the units (4 and 8), resulting in 92. The paragraph also provides examples with three-digit numbers, such as adding 176 and 258, and emphasizes the importance of reviewing old techniques for confirmation.
📝 Mental Math Techniques for Subtraction
The second paragraph focuses on mental math techniques for subtraction. It illustrates how to break numbers into parts and apply a negative sign where necessary. Examples include subtracting 38 from 75 and 56 from 143, showing how to handle negative results and how to combine the results to get the final answer. The paragraph also encourages using long subtraction for confirmation.
🔢 Mental Math Techniques for Multiplication
This paragraph delves into mental multiplication methods. It starts with simple multiplication facts, such as 5 times 4, and explains the concept of 'repeated addition'. The paragraph also covers multiplication of two-digit numbers by breaking them down into simpler components, like 20 times 13, and using the distributive property for calculations like 25 times 7. It provides various strategies, including thinking in terms of money or using the distributive property, to make mental calculations easier.
🔄 Mental Math Techniques for Division
The fourth paragraph covers mental division techniques. It starts with simple division examples, such as dividing 324 by 2 and 168 by 4, and then moves on to more complex examples like 963 divided by 3. The paragraph explains how to break down numbers into divisible parts and use those to find the quotient. It also discusses how to handle numbers that are not easily divisible by breaking them into smaller components, as demonstrated with 156 divided by 4.
🎓 Division Tricks for Quick Calculations
The final paragraph provides additional division tricks for dividing large numbers by one-digit numbers. It suggests breaking down the dividend into parts that are divisible by the divisor. Examples include dividing 234 by 3 and 84 by 7, where the dividend is broken down into parts that can be easily divided by the divisor. The paragraph emphasizes the use of these tricks for quick mental calculations and confirms the results using long division for accuracy.
Mindmap
Keywords
💡Mental Math
💡Breakdown
💡Distributive Property
💡Carry Over
💡Negative Sign
💡Multiplication Tables
💡Repeat Addition
💡Long Division
💡Divisibility
💡Money Analogy
💡Confirmation
Highlights
Mental math techniques are discussed for performing arithmetic operations like addition, subtraction, multiplication, and division in your head quickly and accurately.
Breaking down numbers into smaller components can simplify the addition process. For example, adding 34 and 58 involves adding 30+4 and 50+8 separately, then combining the sums.
When adding three-digit numbers, first add the hundreds, then the tens, and finally the units, combining the results step by step.
Subtraction can be approached similarly by breaking down the minuend and subtrahend into smaller, more manageable parts.
Multiplication can be viewed as repeated addition. For instance, 5 times 4 means adding the number 5 four times.
The distributive property can be used to simplify multiplication, such as multiplying 20 by 13 by breaking it down into (10+3) times 20.
For division, breaking down the dividend into numbers that are divisible by the divisor can make mental calculations easier.
Using multiples and divisibility rules can simplify mental division, such as dividing 168 by 4 by recognizing 16 and 8 as multiples of 4.
Long division can be used to confirm the results of mental math calculations for accuracy.
Money can be used as a conceptual aid in multiplication problems, such as visualizing 13 twenty-dollar bills to find the value of 20 times 13.
The technique of rewriting numbers in a way that simplifies multiplication, such as expressing 99 as (100-1), can be very useful.
When multiplying two-digit numbers, breaking them down into tens and units and multiplying each part can streamline the process.
Carry-over and borrowing techniques are essential for handling numbers larger than 10 in mental arithmetic, especially in subtraction.
Confirming mental math results with a calculator or traditional long multiplication/division is a good practice to ensure accuracy.
Visualizing numbers as combinations of tens, fives, and ones can assist in multiplication, such as imagining seven quarters to find the value of 25 times 7.
For complex division problems, breaking the dividend into smaller, more manageable parts that are easily divisible can simplify the process.
The video provides step-by-step examples and techniques for performing arithmetic operations mentally, making it easier to grasp and apply these methods.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: