Lesson 9 - Introduction To Integrals (Calculus 1 Tutor)

Math and Science
4 Mar 201604:00
EducationalLearning
32 Likes 10 Comments

TLDRThis video script introduces the concept of integration, the second major theme in calculus alongside differentiation. It explains that while taking derivatives is a relatively straightforward process, integration can be more challenging and sometimes requires advanced tools. The script uses the analogy of derivatives to explain how integration, or taking an antiderivative, is essentially the reverse process of differentiation. It emphasizes the importance of understanding integration for applications in engineering and physics, where it is widely used and sometimes only solvable with computer assistance.

Takeaways
  • 📚 The course section focuses on 'Introduction to Integration' or 'Introduction to Integrals', which is a core part of calculus.
  • 🔄 Calculus has two main themes: differentiation (done so far) and integration (the current topic), often referred to as differential and integral calculus.
  • 🎯 While taking derivatives is a relatively straightforward process with established techniques like the chain rule, integration presents more of a challenge.
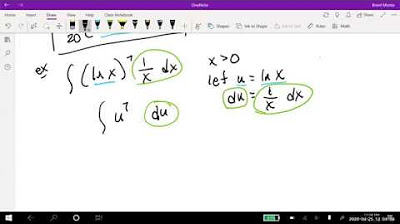
  • 🤔 Integration is the process of finding a function such that its derivative equals a given function, essentially the reverse process of differentiation.
  • 🌐 The concept of an integral is also known as an antiderivative, which is just the opposite of a derivative.
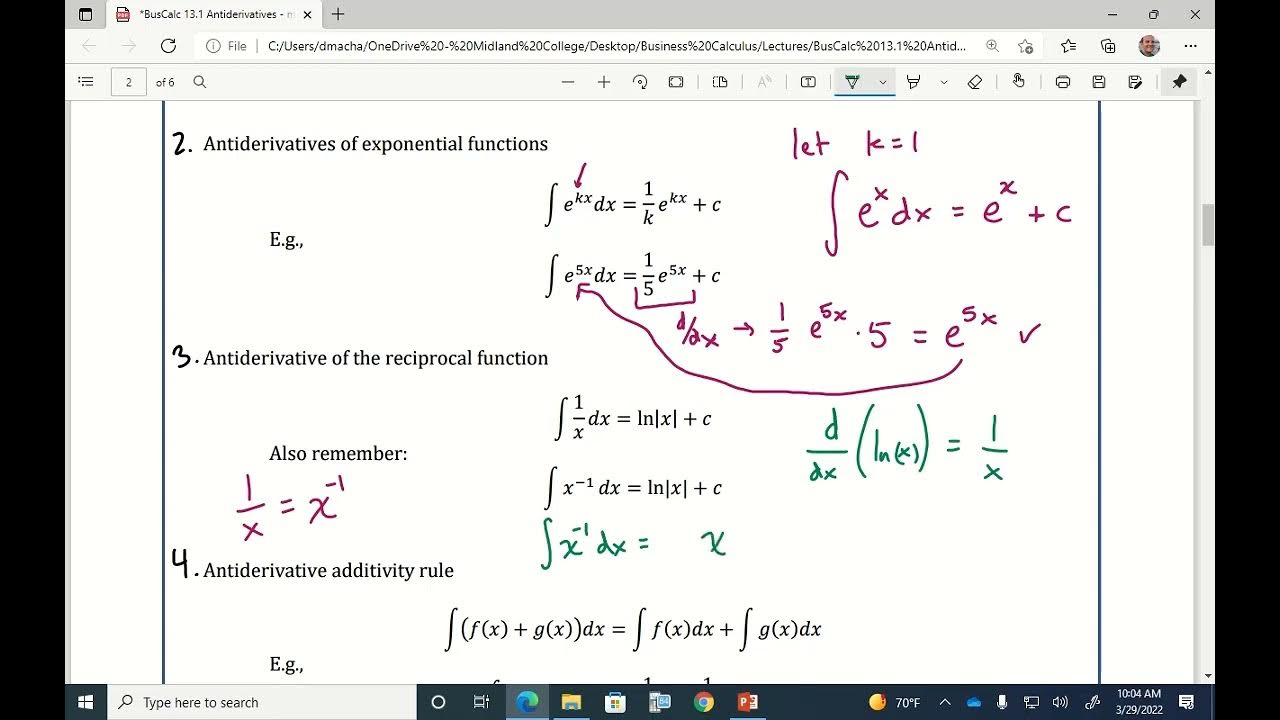
  • 📈 The process of integration is symbolized by the integral sign, which resembles the letter 'S', and is written as ∫f(x)dx, where f(x) is the function being integrated with respect to x.
  • 🔢 The integral of a function 2x over dx is an example used in the script to illustrate the concept of integrating a function.
  • 💡 The usefulness of integrals is highlighted by their widespread application in fields like engineering and physics, where they are indispensable tools.
  • 🚫 Some integrals are so complex that they cannot be solved without the aid of a computer, indicating the depth and challenge of certain mathematical problems.
  • 🛠️ The script emphasizes the importance of understanding the basics of integration to build a solid foundation for further study and application in various fields.
Q & A

  • What are the two main themes in calculus?

    -The two main themes in calculus are differentiation and integration, also known as derivatives and integrals respectively.

  • What is the process of finding the derivative of a function?

    -The process of finding the derivative of a function involves using techniques such as the chain rule, multiplication rule, and division rule to simplify the function until no further differentiation is possible.

  • What is the term used to describe the reverse process of differentiation?

    -The term used to describe the reverse process of differentiation is integration, which is also referred to as finding the antiderivative of a function.

  • What is the significance of integrals in real-life applications such as engineering and physics?

    -Integrals play a crucial role in real-life applications like engineering and physics as they are used to solve problems that involve accumulation of quantities, area under curves, and volumes, among other things.

  • How does the concept of an antiderivative relate to the process of integration?

    -An antiderivative is a function whose derivative is the given function. When integrating, or taking the integral of a function, you are essentially finding its antiderivative.

  • What is the symbol used to represent integration?

    -The symbol used to represent integration is ∫, which resembles the letter 'S'.

  • What is the general notation for writing an integral in a problem?

    -The general notation for writing an integral in a problem is ∫f(x) dx, where f(x) is the function being integrated with respect to the variable x.

  • Why is integration considered more challenging than differentiation?

    -Integration is considered more challenging than differentiation because there isn't always a straightforward, mechanical process to follow. Some integrals have no simple algebraic solution and may require advanced techniques or computational tools.

  • What is an example of a basic integral?

    -An example of a basic integral is finding the antiderivative of the function 2x, which leads to the integral ∫2x dx.

  • How do you interpret the integral ∫2x dx?

    -The integral ∫2x dx represents the process of finding the antiderivative or the function whose derivative is 2x with respect to x.

  • What is the relationship between the derivative of a function and its antiderivative?

    -The derivative of a function and its antiderivative are inverse operations. The derivative gives you the rate of change or slope of the original function, while the antiderivative undoes this process to find the original function.

Outlines
00:00
📚 Introduction to Integration and Its Importance

This paragraph introduces the concept of integration, one of the two main themes in calculus, the other being differentiation. It emphasizes the importance of understanding integration as it is a fundamental part of both engineering and physics. The paragraph explains that while differentiation is relatively straightforward, integration can be more challenging. It sets the stage for learning about integrals by drawing an analogy with derivatives, highlighting that integration is essentially the reverse process of differentiation. The purpose of this section is to build a solid foundation for understanding integrals and their applications.

Mindmap
Keywords
💡Calculus
Calculus is a branch of mathematics that deals with the study of change and motion, primarily through the use of derivatives and integrals. In the video, calculus is introduced as having two main themes: differentiation (which involves finding derivatives) and integration (which involves finding integrals or antiderivatives). The video focuses on the concept of integration, emphasizing its importance and application in various fields such as engineering and physics.
💡Integration
Integration, also known as finding the integral or antiderivative, is the process of determining a function whose derivative is a given function. It is the reverse operation of differentiation and is symbolized by the integral sign, which resembles the letter 'S'. In the context of the video, integration is presented as a more challenging concept compared to differentiation, with some integrals being so complex that they require a computer to solve.
💡Derivative
A derivative is a concept in calculus that represents the rate of change or the slope of a function at a particular point. It is the foundation of differentiation, one of the two main themes in calculus. The video script explains that derivatives can be calculated using various techniques such as the chain rule, and that the process involves taking derivatives repeatedly until nothing more can be derived.
💡Antiderivative
An antiderivative is a function whose derivative is the given function. In other words, it is the reverse process of finding a derivative. The video script introduces the concept of integration as finding the antiderivative, which is essentially the same as finding the integral. This concept is crucial in solving problems where one needs to revert from a derived function back to the original function.
💡Chain Rule
The chain rule is a technique used in calculus to find the derivative of a composite function, which is a function made up of other functions. It involves differentiating the outer function first and then multiplying by the derivative of the inner function. The video script mentions the chain rule as one of the techniques used in differentiation, which is the process of finding the derivative of a function.
💡Slope
The slope of a line is a measure of its steepness, and in the context of a curve, it represents the rate of change at a specific point. In the video, the slope is used to describe the derivative of a function, which gives the slope of the tangent line to the curve at any point of interest. This concept is fundamental in understanding the relationship between a function and its derivative.
💡Engineering
Engineering is a field that applies scientific and mathematical principles to design, build, and maintain structures, machines, systems, and processes. In the video, the importance of integration in engineering is highlighted, as it is a crucial tool for solving real-world problems that engineers encounter. The script mentions that integrals are ubiquitous in engineering, indicating their widespread application and significance in the field.
💡Physics
Physics is the natural science that studies matter, energy, and the fundamental forces of the universe. The video script points out that integrals play a vital role in physics, particularly in understanding and modeling the behavior of physical systems. The integral is essential for calculating quantities such as work, energy, and other physical properties that involve accumulation or summation of effects over time or space.
💡Computer
A computer is an electronic device that manipulates information, or data, using prestored instructions called programs. In the context of the video, computers are mentioned as tools that can help solve complex integrals that are beyond the capabilities of manual calculation. This highlights the role of technology in advancing the field of mathematics, particularly in areas where manual computation is challenging or impractical.
💡Analogies
An analogy is a comparison between two things for the purpose of explanation or clarification. In the video, the instructor uses an analogy from the concept of derivatives to introduce the idea of integration. By drawing parallels between the processes of differentiation and integration, the analogy helps to simplify the understanding of integration as the reverse process of differentiation.
💡Function
A function is a mathematical relation between a set of inputs and a set of permissible outputs. In the context of the video, functions are the central objects of study in calculus, with derivatives and integrals being specific ways of analyzing and transforming these functions. The video script discusses functions such as x squared and 2x, and how their derivatives and integrals can be found using various calculus techniques.
Highlights

Introduction to integration as a core concept in calculus.

Differentiation and integration as the two main themes in calculus.

The process of taking derivatives using techniques like the chain rule and multiplication rule.

Integration being more challenging compared to differentiation.

The existence of integrals that cannot be solved without a computer in real-life applications.

The fundamental concept of an integral as the opposite of a derivative.

Integrals also referred to as antiderivatives.

The process of finding a function whose derivative is given, known as taking an integral.

The integral symbol and its representation in mathematical notation.

The integral as a measure of the area under a curve.

The importance of understanding integration for applications in engineering and physics.

The concept of the antiderivative and its relationship with the interval.

The notation for writing an integral in a problem, including the function and variable.

The potential difficulty in solving certain integrals and the need for a solid foundational understanding.

The practical applications and usefulness of integrals in various fields.

Transcripts

Browse More Related Video

4.1 - Antidifferentiation

Understand Calculus in 35 Minutes

BusCalc 13.1 Antiderivatives

Calculus: Why does integrating a function give area under its curve?

Math 11 - Section 4.5

Antiderivatives

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusIntegrationDifferentialEngineeringPhysicsDerivativesAntiderivativesMathematicsEducationTech