Capacitors - Basic Introduction - Physics
TLDRThe video script offers an insightful explanation of capacitors, emphasizing their function in storing electrical charge through two metal plates separated by an insulator. It delves into the equations governing capacitance, including Q=CV and the concept of charge efficiency, highlighting how capacitance is determined by the construction of the capacitor and not the voltage. The role of dielectric materials in enhancing capacitance and the formula for calculating capacitance are also discussed. The script further illustrates how a battery charges a capacitor by transferring electrons and the subsequent discharge process, where stored energy is used to light up a light bulb. Finally, it introduces equations for calculating the electric potential energy stored in a capacitor.
Takeaways
- 🔋 A capacitor is a device that stores electrical charge using two metal plates separated by an insulator.
- 📏 The charge (Q) stored in a capacitor is directly proportional to its capacitance (C) and the voltage (V) across it, as expressed by the formula Q = CV.
- 📈 Capacitance (C) is measured in farads (F) and represents the charge efficiency of a capacitor, defined as the charge stored per volt.
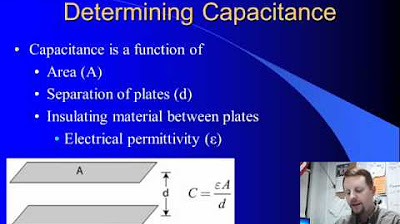
- 🔧 The capacitance of a capacitor is determined by its physical construction, specifically the area of the plates (A) and the separation distance (d), and can be increased by introducing a dielectric material.
- 🌊 The permittivity of free space (ε₀) and the dielectric constant (k) play a crucial role in calculating the capacitance when a dielectric is present, using the formula C = kε₀A/d.
- ⚡ The voltage across a capacitor is the difference in electric potential between its plates and is related to the work done per unit charge.
- 💡 The electric charge is quantized and associated with the quantity of charged particles, such as electrons in metals.
- 🔄 A battery charges a capacitor by driving electrons from one plate to the other, creating an imbalance between protons and electrons, which results in stored charge.
- 💡 The energy stored in a capacitor can be used to power other components, such as light bulbs, by discharging the capacitor through them.
- 🔄 The discharge of a capacitor involves the flow of electrons from the negatively charged plate to the positively charged one until equilibrium is reached.
- 🌟 The electric potential energy stored in a capacitor can be calculated using three formulas: ½QV, ½CV², or Q²/(2C).
Q & A
What is the primary function of a capacitor?
-A capacitor's primary function is to store electrical charge. It does this by using two metal plates separated by an insulator and accumulating charge by moving electrons from one side to the other, effectively creating a positive and negative charge on opposite plates.
How does a capacitor differ from a battery in terms of energy storage?
-A capacitor stores electrical charge through its plates, while a battery stores energy in a chemical form. A battery can provide a steady flow of current, whereas a capacitor is better suited for applications requiring quick bursts of energy.
What is the unit of capacitance and how is it related to charge efficiency?
-The unit of capacitance is the farad (F). One farad is equal to one coulomb per volt. It represents the charge efficiency of a capacitor, indicating the amount of charge a capacitor can store per volt.
How does the capacitance of a capacitor change with varying voltage?
-The capacitance of a capacitor is a constant value determined by its physical construction and does not change with the applied voltage. However, the amount of charge a capacitor can store increases with the increase in voltage, as per the formula Q = CV, where Q is the charge, C is the capacitance, and V is the voltage.
What is the role of the insulator in a capacitor?
-The insulator in a capacitor serves as a separator between the two metal plates and prevents the flow of electrons through the medium, ensuring that the charge is stored on the plates without being dissipated. The insulator can be any material that does not conduct electricity, such as air, paper, or water.
How does the addition of a dielectric material affect the capacitance of a capacitor?
-Adding a dielectric material between the plates of a capacitor increases its capacitance. The dielectric constant (k) of the material determines how much the capacitance increases. The new capacitance (C) with the dielectric is given by the formula C = k * ε₀ * A / d, where ε₀ is the permittivity of free space, A is the area of the plates, and d is the distance between the plates.
What is the relationship between the charge on a capacitor's plates and the number of electrons and protons?
-The charge on a capacitor's plates is directly related to the difference in the number of electrons and protons. If a plate has more protons than electrons, it will have a positive charge, and if it has more electrons than protons, it will have a negative charge.
How does a battery charge a capacitor?
-A battery charges a capacitor by creating a potential difference (voltage) that causes electrons to move from one plate to the other. The battery's electromotive force pushes electrons through the circuit, effectively transferring charge from one side of the capacitor to the other, until the voltage across the capacitor equals the battery voltage.
What happens when a charged capacitor is disconnected from a battery and connected to a load, like a light bulb?
-When a charged capacitor is connected to a load, the stored charge is discharged through the load. Electrons flow from the negatively charged plate to the positively charged plate, passing through the load (like a light bulb), which lights up if the capacitor has sufficient energy. The capacitor continues to discharge until the charge on both plates is balanced, at which point the capacitor is considered discharged.
What are the three formulas to calculate the electric potential energy stored in a capacitor?
-The three formulas to calculate the electric potential energy (U) stored in a capacitor are: U = 1/2 * Q * V (where Q is the charge and V is the voltage), U = 1/2 * C * V^2 (where C is the capacitance), and U = Q^2 / (2 * C) (which can be derived from the first two formulas).
How does the permittivity of free space (ε₀) factor into the capacitance calculation?
-The permittivity of free space (ε₀) is a fundamental constant that appears in the basic formula for capacitance when there is a vacuum between the plates (C = ε₀ * A / d). It is also used in the calculation of the electric field (E = V / d) and the surface charge density (σ = E / ε₀), which are important for understanding the behavior of capacitors.
Outlines
🔋 Understanding Capacitors and Their Function
This paragraph introduces the concept of capacitors, explaining that they store electrical charge using two metal plates separated by an insulator. Unlike batteries, capacitors do not have a power source but instead store charge by moving electrons from one side to the other. The insulator can be various non-conductive materials like air, paper, or water. The fundamental equations related to capacitors are also introduced, such as Q (charge) being equal to CV, where Q is measured in coulombs, C is the capacitance in farads, and V is the voltage in volts. The paragraph emphasizes the importance of understanding the relationship between charge, capacitance, and voltage.
📈 Capacitance and Electric Charge
The second paragraph delves deeper into the concept of capacitance, describing it as a measure of charge efficiency. It explains that the capacitance of a capacitor is determined by its physical construction and is independent of the voltage applied. The explanation includes a comparison of two hypothetical capacitors with different capacitances, illustrating how a higher capacitance allows for more charge to be stored per volt. The paragraph also discusses the discrete nature of electric charge, focusing on electrons as the charge carriers in metals and their individual charge quantity. Additionally, it introduces the concept of electric potential (V) as the ratio between electric potential energy and charge (Q), highlighting the difference between potential and voltage.
🧱 Deriving the Capacitor Formula and the Role of Dielectrics
This paragraph discusses the derivation of the capacitance formula for a capacitor, emphasizing the relationship between capacitance, the area of the plates (A), the separation distance (d), and the permittivity of the material between the plates (ε). It introduces the formula C = ε₀ * A / d, where ε₀ is the permittivity of free space, and explains how adding a dielectric material changes the capacitance and voltage. The paragraph also explains how the dielectric constant (k) affects capacitance and provides examples of different dielectric materials and their respective k values. The impact of adding a dielectric on the stored charge and voltage is clarified, highlighting that while capacitance increases, the voltage decreases proportionally, maintaining the same total charge.
🔋 How a Battery Charges a Capacitor
The fourth paragraph explains the process of how a battery charges a capacitor. It describes the initial state of the capacitor with no charge and equal numbers of electrons and protons on both plates. Upon connecting the capacitor to a battery, the voltage difference causes electrons to flow from the plate with excess electrons (negatively charged) to the plate deficient of electrons (positively charged). Over time, this flow of electrons results in the accumulation of charge on the plates, which corresponds to the voltage of the battery. The paragraph illustrates this process with an example, showing how the charge on the plates changes as electrons move and how the capacitor's charge corresponds to the product of the charge per electron and the number of electrons transferred.
💡 Discharging a Capacitor and Energy Storage
The final paragraph discusses the discharging process of a capacitor and the storage of electric potential energy. It explains that when a charged capacitor is connected to a load, such as a light bulb, electrons flow from the negatively charged plate to the positively charged plate, causing the light bulb to illuminate if the capacitor has sufficient energy. The discharging process continues until the electron count on both plates equals out, at which point the capacitor is considered discharged. The paragraph also presents three key equations for calculating the potential energy stored in a capacitor: ½QV, ½CV², and ½Q(V/C), providing a comprehensive understanding of energy storage and release in capacitors.
Mindmap
Keywords
💡Capacitor
💡Electric Charge
💡Capacitance
💡Voltage
💡Dielectric
💡Electric Potential
💡Surface Charge Density
💡Permittivity of Free Space
💡Energy Storage
💡Discharge
Highlights
A capacitor stores electrical charge, differing from a battery in its function and construction.
Capacitors consist of two metal plates separated by an insulator, which can be various non-conductive materials like air, paper, or water.
The charge (Q) stored in a capacitor can be calculated using the formula Q = CV, where C is the capacitance and V is the voltage.
Capacitance (C) is measured in farads and represents the charge efficiency of a capacitor, indicating the amount of charge it can hold per volt.
The capacitance of a capacitor is determined by its physical construction, specifically the area of the plates (A) and the distance between them (d), and is independent of the voltage.
Adding a dielectric material between the plates of a capacitor increases its capacitance (C) and changes the voltage (V) across it, but the total charge (Q) remains constant.
The permittivity of free space (ε₀) is a fundamental constant in the equation for capacitance when a vacuum is the dielectric, and it is approximately 8.85 × 10^-12 F/m.
The capacitance of a capacitor can be calculated using the formula C = ε₀ * A / d for vacuum dielectric, and C = ε_r * ε₀ * A / d when a dielectric is present.
The electric field (E) between the plates of a capacitor is determined by the voltage (V) and the separation distance (d), with E = V/d.
A capacitor is charged by a battery through the flow of electrons from one plate to the other, creating an electric potential difference.
Once charged, a capacitor can be disconnected from the battery and still maintain its charge, which can be used to power other components like light bulbs.
The electric potential energy stored in a capacitor can be calculated using the formulas 0.5QV, 0.5CV^2, or Q^2/(2C).
The process of charging and discharging a capacitor demonstrates the principles of electron movement and electric potential difference.
Capacitors play a crucial role in electronic circuits by regulating voltage, filtering signals, and providing temporary energy storage.
Understanding the relationship between charge, capacitance, and voltage is essential for designing and analyzing electronic circuits.
The properties of dielectric materials significantly influence the performance and capacitance of capacitors in electronic applications.
The quantization of electric charge, with electrons having a discrete charge of -1.6 × 10^-19 C, is a fundamental concept in the study of capacitors and electronics.
The derivation of the capacitance formula from basic principles of electric fields and charge distribution provides insight into the physical workings of capacitors.
Practical applications of capacitors include their use in power supplies, signal processing, and energy storage, showcasing their versatility in electronic systems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: