Kirchhoff's Laws - A-level Physics

Science Shorts
9 Jan 202007:13
EducationalLearning
32 Likes 10 Comments

TLDRThe video script offers a comprehensive review of Kirchhoff's Laws, emphasizing their fundamental role in understanding electrical circuits. It corrects the pronunciation of 'Kirchhoff' and delves into the two key laws: the conservation of current at junctions and the relationship between electromotive force (EMF) and potential difference (PD) drops in a closed loop. The script uses various examples, from simple to complex, to illustrate how these laws apply in different circuit configurations, highlighting the importance of considering the direction and division of currents and EMFs in a network.

Takeaways
  • 🎓 Kirchhoff's Laws are fundamental for understanding electricity and circuits.
  • 🔄 Kirchhoff's First Law states that the total current entering a junction must equal the total current leaving it, highlighting the conservation of current at junctions.
  • 🔋 The Second Law indicates that in any closed loop, the total electromotive force (EMF) is equal to the sum of potential difference (PD) drops.
  • 📊 Practical applications of these laws can be seen in solving complex circuit diagrams with multiple branches.
  • 🔄 When dealing with circuits, it's crucial to remember that the direction of current flow is not always obvious and may need to be specified.
  • 🔩 In a branching circuit, the potential difference across resistors can be determined by applying Kirchhoff's Laws to individual loops and the overall circuit.
  • 🔄 The presence of multiple EMFs in a circuit can lead to situations where the EMFs do not simply add up, as they may oppose each other.
  • 📈 The potential divider equation is used to determine voltage distribution in a loop with a single EMF source and resistors.
  • 🔄 When additional resistors are introduced into a circuit, the distribution of current and voltage changes, requiring re-evaluation of the circuit's behavior.
  • 🔌 The current through a resistor can be calculated using Ohm's Law (I = V/R), but the voltage (V) must be accurately determined first.
  • 🤔 Solving circuit problems often involves breaking down the circuit into simpler loops and applying Kirchhoff's Laws to each loop to understand the overall behavior.
Q & A

  • What was the main issue with the speaker's first video on Kirchhoff's law?

    -The main issue with the speaker's first video on Kirchhoff's law was the mispronunciation of Kirchhoff's name and potentially not explaining the laws as clearly as possible.

  • What are Kirchhoff's two laws mentioned in the video?

    -Kirchhoff's two laws mentioned are: 1) Kirchhoff's Current Law, which states that the total current entering a junction is equal to the total current leaving it, and 2) Kirchhoff's Voltage Law, which states that in any closed loop, the total EMF is equal to the sum of the PD drops.

  • Why is Kirchhoff's Current Law considered useful?

    -Kirchhoff's Current Law is considered useful because it applies to junctions with multiple branches, helping to analyze complex circuits by ensuring the conservation of current at junctions.

  • How does the speaker demonstrate the first law with an example?

    -The speaker demonstrates the first law by showing that if there are two currents going into a junction (i1 and i2), they must be equal to the sum of the currents leaving the junction (i3, i4, and i5), thus illustrating the conservation of current.

  • What is the basic concept behind Kirchhoff's Voltage Law?

    -The basic concept behind Kirchhoff's Voltage Law is that in a closed loop, the total electromotive force (EMF) is equal to the sum of the potential difference (PD) drops across all components in the loop, which is a statement of energy conservation.

  • How does the speaker explain the concept of EMF in a simple circuit?

    -The speaker explains that in a simple circuit with an EMF source (like a battery) and a resistor, the voltage (V) across the resistor must be equal to the EMF if there is no other opposing force.

  • What happens when multiple EMF sources are connected in the circuit?

    -When multiple EMF sources are connected, their total EMF is the algebraic sum of their individual EMFs, considering their direction. This affects how the potential difference is distributed across resistors in the circuit.

  • How does the speaker use Kirchhoff's second law to solve a circuit with two EMFs and resistors?

    -The speaker uses Kirchhoff's second law to identify the loops in the circuit, calculate the PD drops across each resistor, and then determine the current flow through each branch by considering the total EMF and PD drops in each loop.

  • What formula does the speaker use to calculate the current through a resistor?

    -The speaker uses Ohm's Law, which states that the current (I) through a resistor is equal to the voltage (V) across it divided by the resistance (R), or I = V/R.

  • How does the addition of a third resistor affect the analysis of the circuit?

    -The addition of a third resistor complicates the circuit further, changing the distribution of EMF and PD drops across all resistors. It requires re-evaluating the current flow and PD across each resistor, considering the new loop formed by the third resistor.

  • What is the significance of understanding Kirchhoff's laws in electrical engineering?

    -Understanding Kirchhoff's laws is crucial in electrical engineering as they form the basis for analyzing and designing complex electrical circuits, ensuring the conservation of energy and current, which are fundamental principles in the field.

Outlines
00:00
📚 Introduction to Kirchhoff's Laws

The paragraph begins with an acknowledgment of a previous video's shortcomings, particularly in the pronunciation of Kirchhoff's name. It then introduces Kirchhoff's two laws for electricity. The first law states that the total current entering a junction equals the total current leaving it, emphasizing the conservation of current at junctions. The explanation includes a hypothetical scenario with multiple currents (i1, i2, i3, i-4, i-5) and how they relate to each other based on the law. The second law is introduced as the principle that the total electromotive force (EMF) in any closed loop network is equal to the sum of potential difference (PD) drops. This is illustrated with examples of simple circuits and the behavior of EMF in different configurations, including the directional nature of EMF and how it affects the PD across resistors.

05:03
🔌 Applying Kirchhoff's Laws to Complex Circuits

This paragraph delves into the application of Kirchhoff's laws in more complex circuit scenarios, particularly those involving branching and parallel circuits. It starts with a detailed example of a circuit with two EMFs and varying resistances, explaining how to identify loops and calculate the PD across resistors using Kirchhoff's second law. The explanation includes the concept of potential dividers and how they relate to the overall EMF of the circuit. The paragraph then addresses the challenges of determining current flow in branched circuits and introduces a method for calculating unknown currents based on known values and the law of conservation at junctions. It concludes with a hypothetical addition of another resistor and the implications it has on the distribution of EMF and PD across the circuit.

Mindmap
Keywords
💡Kirchhoff's Laws
Kirchhoff's Laws are fundamental principles used in electrical circuit analysis, formulated by Gustav Kirchhoff. The video discusses these laws as a basis for understanding current and voltage relationships in circuits. The first law, the Current Law, states that the total current entering a junction is equal to the total current leaving it. The second law, the Voltage Law, asserts that the total electromotive force (EMF) in a closed loop is equal to the sum of potential differences (PD). These laws are essential for analyzing complex circuits with branches, as demonstrated in the video with various examples.
💡Current Conservation
Current Conservation is a concept derived from Kirchhoff's Current Law, which states that current is conserved at junctions. This means that the algebraic sum of currents entering and leaving a point in a circuit is zero. This principle is crucial for solving for unknown currents in a circuit and is a fundamental concept in the analysis of electrical networks.
💡EMF (Electromotive Force)
Electromotive Force (EMF) is the energy provided by a power source, such as a battery or cell, that drives the flow of electrons in a circuit. EMF is measured in volts and represents the work done per unit charge to move electrons from the low potential terminal to the high potential terminal of the power source. In the context of the video, EMF is a key factor in understanding the behavior of closed loops and how the total EMF in a loop equals the sum of PD drops across the components.
💡PD (Potential Difference)
Potential Difference (PD), also known as voltage, is the measure of the electric potential between two points in a circuit. It represents the work done per unit charge in moving an electric charge from one point to another. PD is a crucial concept in understanding how electrical energy is converted to other forms of energy, such as heat in resistors. The video emphasizes the relationship between EMF and PD, particularly in the context of Kirchhoff's Voltage Law.
💡Circuit Analysis
Circuit Analysis refers to the process of determining the behavior of electrical circuits by applying physical laws and mathematical methods. It involves understanding how various components, such as resistors, capacitors, inductors, and power sources, interact with each other. The video focuses on using Kirchhoff's Laws as fundamental tools for analyzing and solving for currents, voltages, and other quantities of interest in electrical circuits.
💡Resistors
Resistors are passive electrical components that limit or regulate the flow of electric current in a circuit. They dissipate electrical energy in the form of heat, and their action is characterized by their resistance value, measured in ohms. Resistors play a key role in determining the current and voltage distribution in a circuit and are essential components in the analysis of circuits using Kirchhoff's Laws.
💡Ohm's Law
Ohm's Law is a fundamental principle that relates the voltage (V), current (I), and resistance (R) in a circuit. It states that the voltage across a resistor is directly proportional to the current through it, with the resistance being the constant of proportionality. This law is crucial for analyzing the behavior of resistors in a circuit and is used extensively in the video to calculate currents and voltages.
💡Circuit Diagrams
Circuit diagrams are visual representations of electrical circuits that show the connections between various components. They are essential tools for understanding, designing, and troubleshooting electrical systems. The video script refers to circuit diagrams as a means of illustrating the application of Kirchhoff's Laws and Ohm's Law in analyzing the flow of current and voltage in different types of circuits.
💡Junction
In the context of electrical circuits, a junction refers to a point where two or more circuit elements, such as resistors or wires, meet. Junctions are important in circuit analysis because they are the points where currents can split or combine. Kirchhoff's Current Law specifically deals with the behavior of currents at junctions, stating that the total current entering a junction must equal the total current leaving it.
💡Loop
A loop in an electrical circuit is a closed conducting path through which electric current can flow. Loops are significant in circuit analysis because they allow for the application of Kirchhoff's Voltage Law, which states that the total EMF in a closed loop is equal to the sum of PD drops across the components in the loop. Understanding loops is crucial for analyzing circuits with multiple paths for current flow.
💡Branching Circuits
Branching circuits are circuits that split into two or more paths, allowing the current to flow through different components. These circuits add complexity to circuit analysis because the current must be divided among the branches, and the voltage drops across each branch component must be considered. The video script uses branching circuits to illustrate the application of Kirchhoff's Laws and Ohm's Law in determining the current and voltage distribution in more complex electrical networks.
Highlights

Introduction to Kirchhoff's Laws and acknowledgment of a previous mispronunciation.

Kirchhoff's First Law states that the total current entering a junction is equal to the total current leaving it, emphasizing the conservation of current at junctions.

Explanation that the conservation of current might seem obvious but is very useful in circuit analysis.

Kirchhoff's Second Law explains that in any closed loop, the total EMF is equal to the sum of PD drops.

Illustration of how EMF and PD drops function in simple circuits with one cell or battery.

Discussion on how the direction of EMF from batteries and cells affects the total EMF in a circuit.

Use of Kirchhoff's Second Law in more complex circuits with branching and parallel arrangements.

Explanation of how to calculate PD across resistors in a circuit with multiple loops.

Demonstration of calculating the current through a resistor using Ohm's law and the PD across it.

Application of Kirchhoff's Laws to determine the current in a branched circuit.

Explanation of how adding another resistor changes the total EMF and PD distribution in a circuit.

Insight into how the PD across resistors is affected by the presence of multiple resistors in the same loop.

Clarification that the voltage across resistors cannot be simply split according to their resistances in a branched circuit.

Example of calculating the current in a specific branch using Kirchhoff's Laws and Ohm's law.

Discussion on the complexity introduced by adding additional resistors and how it affects the overall circuit analysis.

Conclusion summarizing the basic concepts of Kirchhoff's Laws and their importance in understanding circuit behavior.

Invitation for feedback and suggestions for future content improvement.

Transcripts

Browse More Related Video

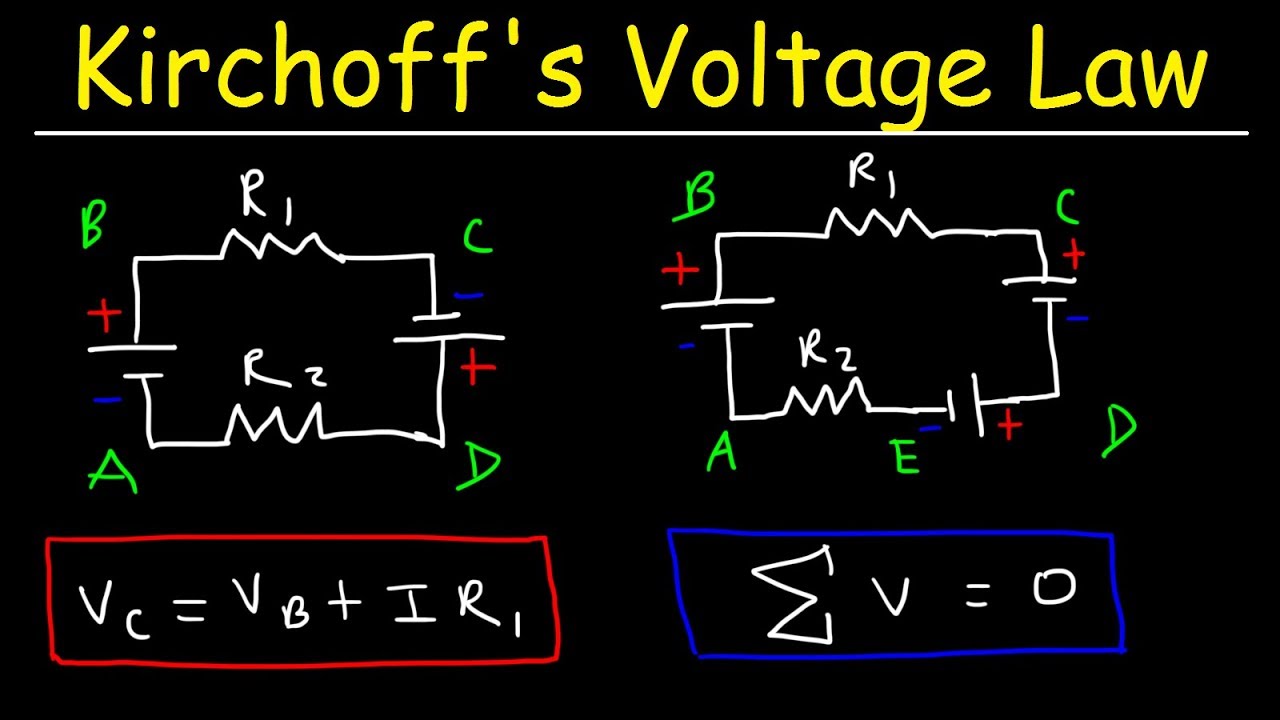
Kirchhoff's Voltage Law - KVL Circuits, Loop Rule & Ohm's Law - Series Circuits, Physics

Kirchhoff's Voltage Law (KVL) Explained

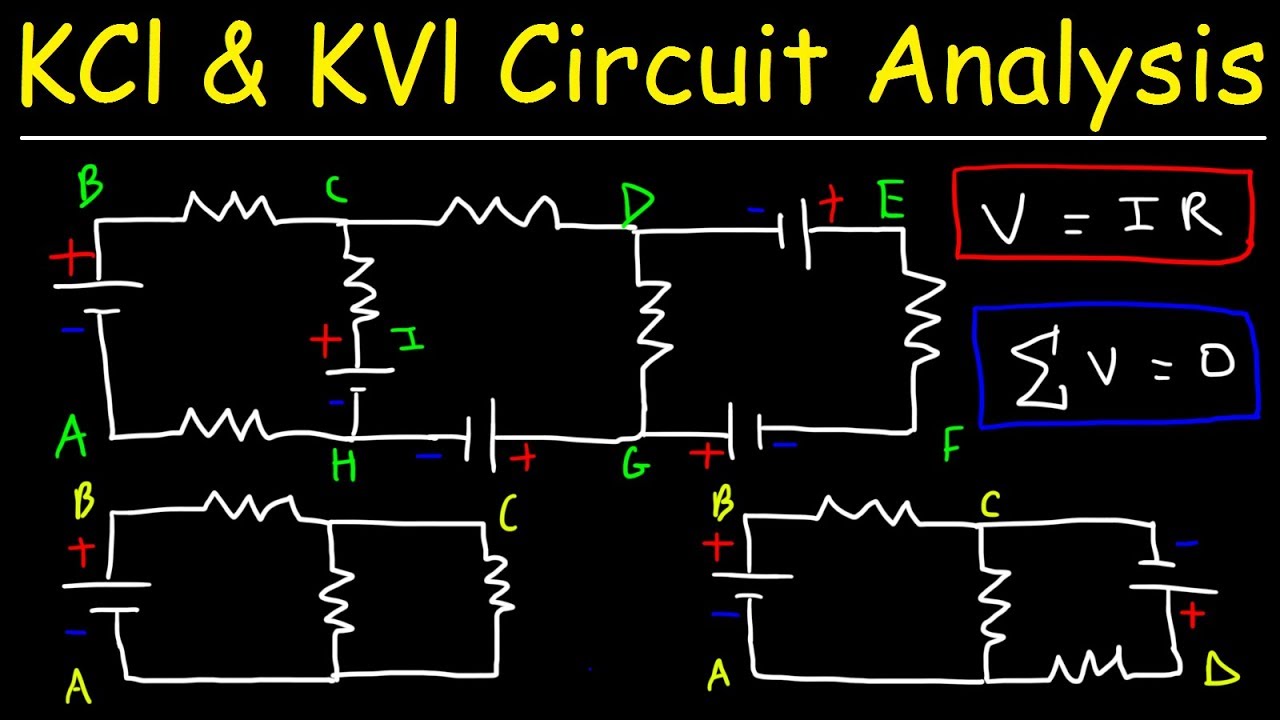
Kirchhoff's Law, Junction & Loop Rule, Ohm's Law - KCl & KVl Circuit Analysis - Physics

Ohm's Law

Capacitors and Kirchhoff: Crash Course Physics #31

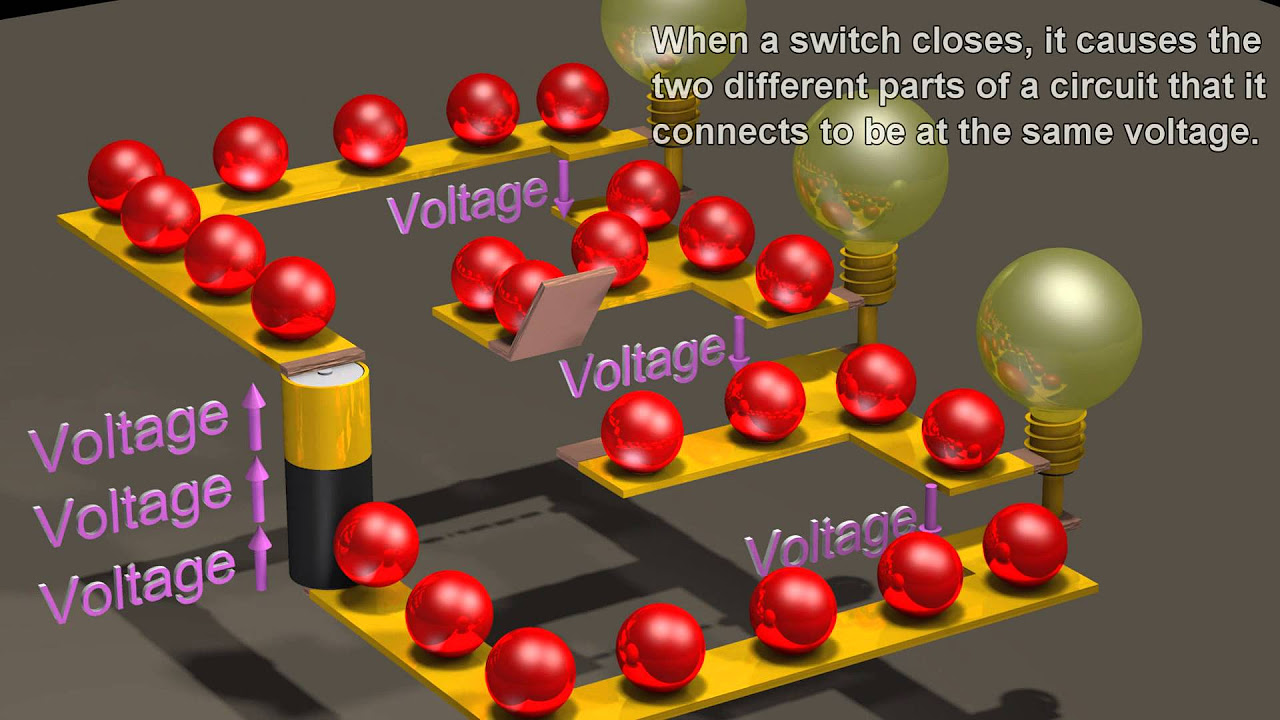
Electric Circuits: Basics of the voltage and current laws.

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Kirchhoff's LawsElectrical CircuitsPhysics EducationCurrent ConservationEMF RelationshipsPractical ExamplesEngineering ConceptsSTEM LearningTutorial VideoEducational Content