4.1 - Antidifferentiation
TLDRThe video script offers a comprehensive introduction to the concept of anti-differentiation, also known as integration. It explains that anti-differentiation is essentially the reverse process of differentiation, aiming to find the original function given its derivative. The script covers various techniques and rules for finding anti-derivatives, including the power rule, constant rule, and special cases like logarithms and exponentials. It also discusses the constant of integration, emphasizing its importance in representing a family of solutions that differ by a constant. The video further illustrates how to apply these rules through several examples, highlighting the process of reversing differentiation to find the original function. Additionally, the script touches on practical applications, such as using velocity functions to determine position functions in physics problems, and demonstrates how to solve for a specific function given an initial condition. The summary also teases upcoming topics that will delve deeper into the meaning of anti-derivatives from a geometric perspective.
Takeaways
- 🔁 **Anti-differentiation** is the process of reversing differentiation to find the original function from its derivative.
- ⚙️ **Integration** is another term for anti-differentiation, often used interchangeably, and symbolized by ∫.
- 📈 **Derivatives and Anti-derivatives** are related such that the derivative of a function plus a constant results in the original function when integrated.
- 😕 **Constant of Integration (C)** is added when finding an anti-derivative because differentiating a constant gives zero, and it may reappear upon integration.
- 📚 **Indefinite Integral** represents the family of anti-derivatives of a function, which includes an arbitrary constant C.
- 📝 **dx** in the integral notation indicates the variable of integration, signifying a small change in the variable x.
- 🔢 **Power Rule for Anti-derivatives** states that when integrating a function of x raised to a power n, you increase the exponent by one and divide by the new exponent, plus add a constant C.
- ➗ **Special Cases** like e^x and 1/x have unique anti-derivatives that are the same or related to their original functions.
- 🔄 **Anti-derivative Rules** are similar to derivative rules but in reverse, allowing for integration of various functions by applying these rules in reverse.
- 📌 **Initial Conditions** can be used to solve for the constant of integration, providing a specific function from the family of anti-derivatives.
- 📈 **Applications** of anti-derivatives include physics problems, such as finding position functions from velocity functions, using the relationship between these quantities.
Q & A
What is anti-differentiation?
-Anti-differentiation, also known as integration, is the process of reversing differentiation. It involves finding a function that, when differentiated, yields a given derivative.
What is the symbol used to represent integration or anti-differentiation?
-The symbol used to represent integration or anti-differentiation is ∫, which is an 'S' shaped symbol, often referred to as the integral symbol.
Why is the constant of integration, typically denoted as 'c', necessary in anti-derivatives?
-The constant of integration is necessary because when a constant is differentiated, it goes to zero and disappears. However, when reversing the process (anti-differentiating), the constant can reappear, representing the family of functions that could have produced the given derivative.
What is the relationship between the derivative of a function and its anti-derivative?
-The derivative of a function gives you the rate of change of the function, while the anti-derivative (or integral) of a function gives you the original function that would result in the given derivative when differentiated.
How does the power rule for differentiation relate to the power rule for anti-differentiation?
-The power rule for anti-differentiation reverses the operations of the power rule for differentiation. Instead of multiplying by the exponent and then decreasing it, you increase the exponent by one and then divide by the new exponent.
What is an indefinite integral, and how is it represented?
-An indefinite integral is the general antiderivative of a function, representing a family of functions that differ by a constant. It is represented using the integral symbol ∫ followed by the function and the differential dx, indicating the variable with respect to which the integration is performed.
How can you find the antiderivative of a constant function with respect to x?
-The antiderivative of a constant function with respect to x is found by multiplying the constant by x and then adding the constant of integration, c.
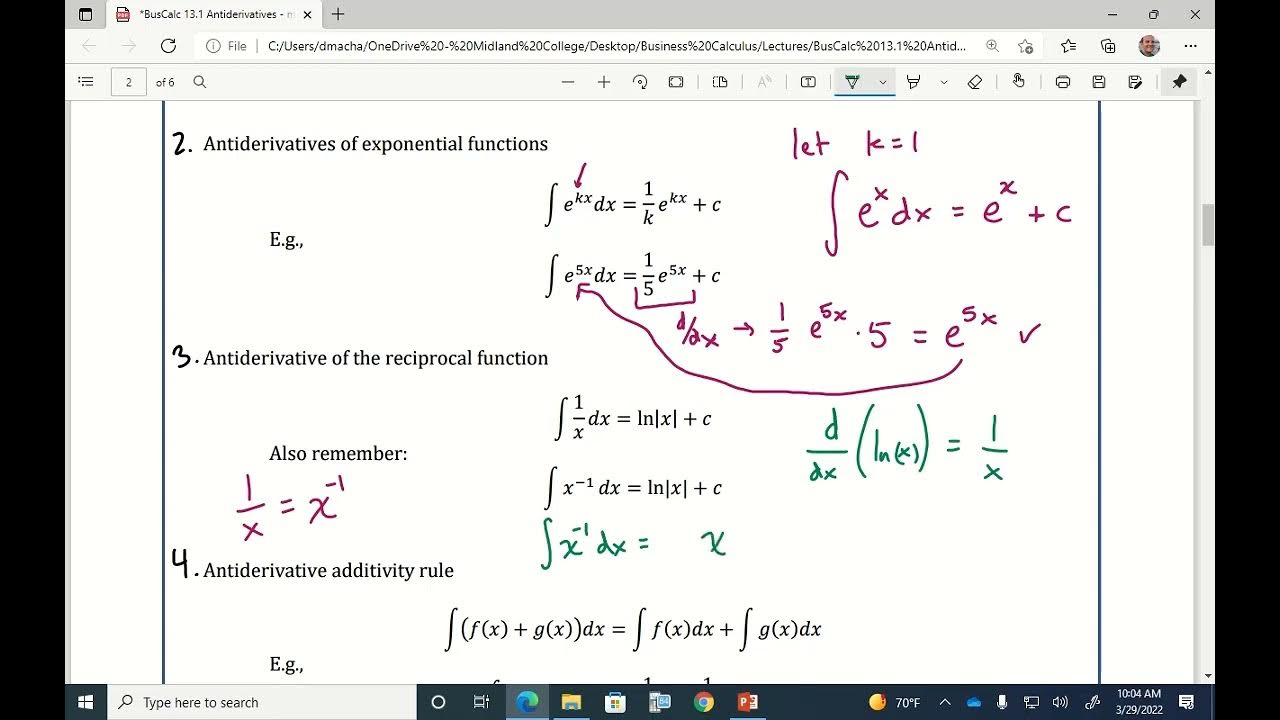
What is the antiderivative of e^x with respect to x?
-The antiderivative of e^x with respect to x is e^x + c, since e^x is its own derivative and anti-derivative.
What is the antiderivative of 1/x (x to the power of -1) with respect to x?
-The antiderivative of 1/x (or x to the power of -1) with respect to x is the natural logarithm of the absolute value of x, ln|x| + c, because the natural logarithm function results in 1/x when differentiated.
How can you check if your antiderivative is correct?
-You can check if your antiderivative is correct by differentiating it again with respect to x. If the result is the original function whose antiderivative you were finding, then your antiderivative is correct.
What is the significance of the constant of integration 'c' in the context of a specific problem?
-In the context of a specific problem, the constant of integration 'c' can be determined if an initial condition, such as a point on the graph of the function, is provided. This allows for the calculation of the exact value of 'c' that makes the antiderivative satisfy the given condition.
Outlines
🔁 Introduction to Anti-differentiation
The video introduces the concept of anti-differentiation as the reverse process of differentiation. It discusses how differentiation provides us with the derivative of a function, and anti-differentiation allows us to find the original function from its derivative. The process involves various techniques and applications, such as finding the function that yields a given derivative, which is called the anti-derivative. The video also explains the notation used for anti-differentiation, including the integral symbol and the constant of integration.
📏 The Role of Constants in Anti-differentiation
This paragraph explains the importance of constants in anti-derivatives. When a function is differentiated, constants disappear (as their derivative is zero), but when finding an anti-derivative, an unknown constant reappears. The video uses the term 'indefinite integral' to describe the process of finding an anti-derivative and introduces the differential 'dx', which signifies the variable of integration. It also covers how to calculate anti-derivatives of constant functions and how to check the results by differentiating the antiderivative.
🔢 Power Rule and Special Cases in Anti-differentiation
The video covers the power rule for anti-differentiation, which reverses the process of the power rule for differentiation. It explains how to find anti-derivatives of functions raised to a power, including the special cases of exponential functions (e^x) and the natural logarithm function (ln(x)). The video emphasizes the need to include the constant of integration 'c' with every anti-derivative and discusses the use of absolute value when dealing with the natural logarithm.
➗ Anti-differentiation of Functions with Fractional Exponents
This part of the video explains how to anti-differentiate functions with fractional exponents, such as square roots and other fractional powers. It demonstrates the process of converting these to exponential form, applying the power rule in reverse by increasing the exponent and dividing by the new exponent, and then simplifying the result. The video also shows how to handle negative exponents and the special case of an exponent of -1, which results in a logarithmic function rather than an exponential one.
🔃 Applying Anti-derivative Rules for Various Functions
The video provides a series of examples to illustrate the application of anti-derivative rules for various functions, including constants, powers, and logarithms. It shows how to combine these rules to find anti-derivatives of more complex functions. The video also discusses the constant rule for anti-differentiation, which allows for the factoring out of constants, and the process of checking anti-derivatives by differentiating them.
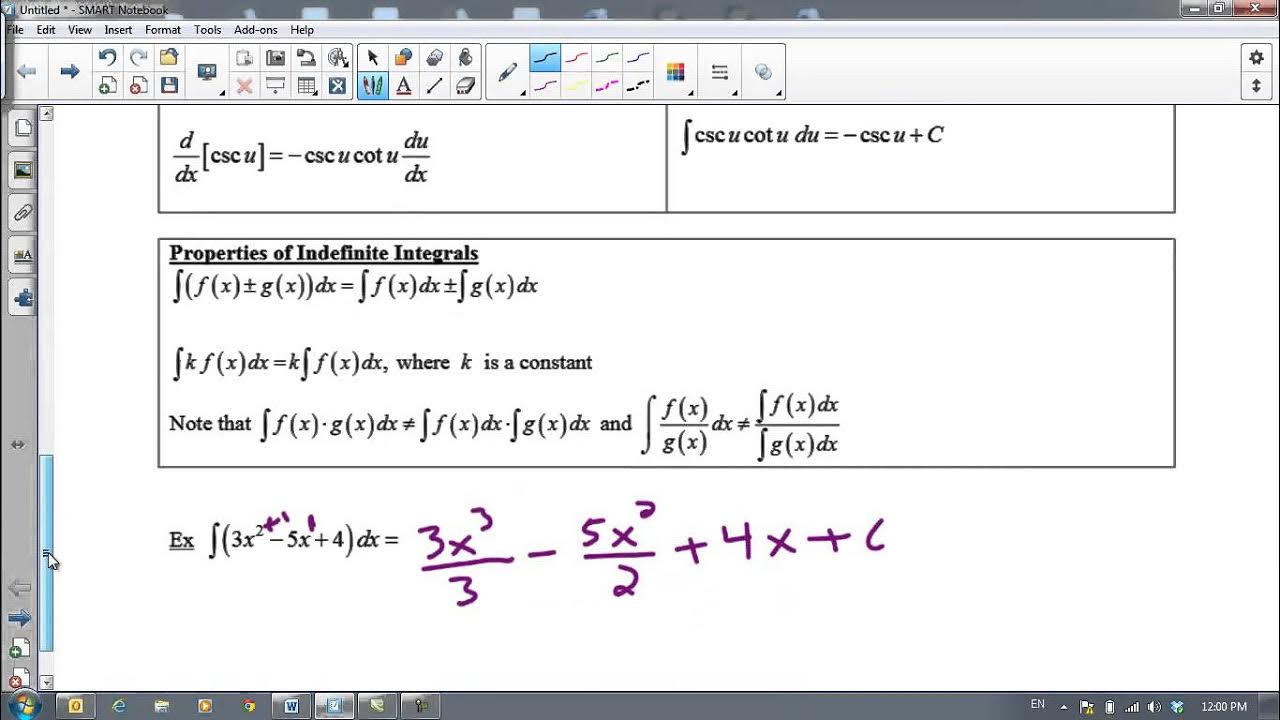
📚 Sums, Differences, and Constant Multiples in Anti-differentiation
This paragraph focuses on the rules for anti-differentiating sums and differences of functions, as well as functions that are constant multiples of other functions. The video explains that each term in a sum or difference can be anti-differentiated separately, and that a constant multiple can be factored out of the integral. The video also provides examples of how to apply these rules to find anti-derivatives of more complicated functions.
🔍 Anti-derivatives and Initial Conditions
The video discusses how an initial condition can be used to find a specific value of the constant of integration 'c' in an anti-derivative. It explains that an initial condition is an additional piece of information that specifies a point on the graph of the function, which can be used to solve for 'c'. The video provides an example where the derivative is given, along with an initial condition, to find the exact function.
🚀 Applied Context: Finding Position from Velocity
The video concludes with an applied context of anti-differentiation, specifically in physics. It uses the example of a rock thrown upward to demonstrate how to find the position function from a given velocity function. The video shows how to anti-differentiate the velocity function to get the position function and then uses an initial condition (the initial height) to find the specific value of the constant of integration. Finally, it calculates the height and velocity of the rock after a certain time.
📈 Final Summary and Preview of Future Topics
The final paragraph summarizes the key points about anti-derivatives and integration covered in the video. It mentions that future videos will explore additional rules for finding anti-derivatives, the meaning of anti-derivatives in different contexts, and the geometric interpretation of anti-derivatives, similar to how derivatives have a specific geometric meaning.
Mindmap
Keywords
💡Anti-differentiation
💡Derivative
💡Constant of Integration
💡Indefinite Integral
💡Integration
💡Power Rule
💡Exponential Function
💡Natural Logarithm
💡Initial Condition
💡Position and Velocity
Highlights
Anti-differentiation is the process of reversing differentiation to find the original function that resulted in a given derivative.
The process of anti-differentiation can be referred to as integration, which is used to find areas under curves and solve various applied problems.
The antiderivative of a function includes an unknown constant, known as the constant of integration, which represents the family of solutions differing by a constant.
The symbol for integration or anti-differentiation is an 'S', which is used to denote the process of finding an antiderivative.
Differentiating a constant results in zero, but when integrating, the constant reappears, which is why the constant of integration is included in every antiderivative found.
The indefinite integral represents the problem being solved and includes the differential 'dx', indicating the variable of integration.
Anti-derivatives can be calculated using known derivative rules in reverse, such as the power rule for anti-differentiation.
Special functions like e^x and 1/x have unique anti-derivatives that are the same or related to their derivatives.
The absolute value is used with the natural logarithm function to ensure the argument is positive, as logarithms are only defined for positive inputs.
Anti-derivative rules are similar to derivative rules but are applied in reverse to find the original function from its derivative.
The constant multiple rule allows a constant to be factored out of an integral, as it does not affect the antiderivative.
Sums and differences in a function can be integrated term by term, allowing for the simplification of complex integrals.
An initial condition can be used to solve for the specific value of the constant of integration, providing a unique solution to an otherwise family of solutions.
In applied contexts, such as physics, anti-derivatives are used to find position functions from velocity functions, which is crucial for understanding motion.
The process of anti-differentiation can be checked by differentiating the result to ensure it matches the original function.
The constant of integration, 'c', represents all possible anti-derivatives that differ by a constant, highlighting the generality of the antiderivative solution.
The concept of anti-derivatives extends to understanding geometric and physical contexts, such as areas under curves and motion analysis.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: