Resistivity and Resistance Formula, Conductivity, Temperature Coefficient, Physics Problems
TLDRThis informative video delves into the concepts of resistivity and resistance in wires, explaining how these properties affect the flow of electricity. It clarifies that longer and thinner wires have higher resistance due to increased length and reduced cross-sectional area. The video also discusses the impact of temperature on resistivity, showing that metals' resistivity increases with temperature, unlike semiconductors. It uses examples and analogies, such as comparing thin and thick wires to lanes of a highway, to illustrate these concepts. Additionally, it provides a step-by-step guide to calculating resistance and voltage drop, using copper wires as examples. Understanding these principles is crucial for applications like digital thermometers that measure temperature based on resistance changes.
Takeaways
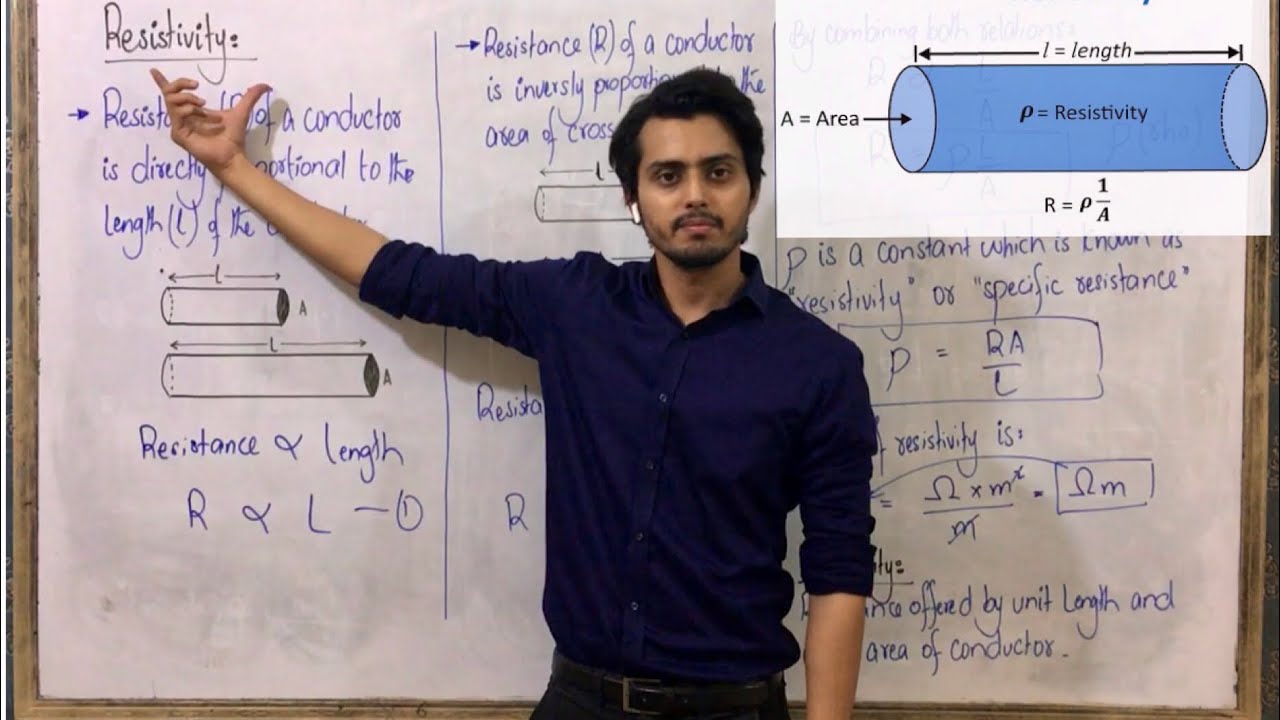
- 📐 The resistance of a wire is calculated using the formula: Resistance (R) = Resistivity (ρ) * Length (L) / Area (A).
- 📈 Long wires have more resistance than short wires due to the direct proportionality between length (L) and resistance in the formula.
- 📊 Thin wires have higher resistance than thick wires because the area (A) in the denominator inversely affects the resistance value.
- 🔌 The resistivity (ρ) is a material property that indicates how strongly a material opposes the flow of electric current.
- 🥇 Silver is a better conductor than copper, as it has a lower resistivity value, making it more conductive.
- 🔩 Materials with low resistivity are good electrical conductors, while those with high resistivity are insulators or semiconductors.
- 🌡️ Resistivity is temperature-dependent, with metals generally having a positive temperature coefficient and semiconductors having a negative one.
- 🔥 For metals, increasing temperature results in increased resistivity and decreased conductivity, while for semiconductors, the opposite is true.
- 🌡️ Resistance can be used to measure temperature; as temperature changes, the resistance of a material changes, allowing for temperature calculation based on known resistivity values.
- 🔧 The voltage drop across a wire can be calculated using Ohm's Law: Voltage (V) = Current (I) * Resistance (R).
- 🔄 When the current through a wire decreases while the voltage remains constant, it indicates an increase in resistance and thus an increase in temperature for metallic conductors.
Q & A
What is the formula to calculate the resistance of a wire?
-The resistance of a wire can be calculated using the formula R = ρ * L / A, where R is the resistance, ρ (rho) is the resistivity of the material, L is the length of the wire, and A is the cross-sectional area.
How does the length of a wire affect its resistance?
-The resistance of a wire increases with its length. This is because the length (L) is in the numerator of the resistance formula. As the length increases, the value of the fraction (and thus the resistance) also increases.
Does a thin wire or a thick wire have more resistance if they have the same length?
-A thin wire has more resistance than a thick wire if they have the same length. This is because the cross-sectional area (A) is in the denominator of the resistance formula. A smaller area results in a larger resistance value.
Why does a thick wire have less resistance than a thin wire?
-A thick wire has less resistance because it provides more space for electrons to move. This increased space allows more electrons to flow, resulting in a lower resistance, similar to how a wider highway can accommodate more traffic.
Which metal is a better conductor, silver or copper, based on resistivity values?
-Silver is a better conductor than copper because it has a lower resistivity value. Lower resistivity indicates better conductivity.
How does the resistivity of a metal change with temperature?
-The resistivity of a metal increases with temperature. This is because the free electrons collide more frequently at higher temperatures, reducing their drift velocity and increasing the metal's resistance.
What happens to the conductivity of metals at low temperatures?
-At low temperatures, metals conduct electricity better because their resistivity decreases. If a metal is cooled enough, it can even become a superconductor with virtually no resistance.
How can the temperature of an object be measured using resistance?
-The temperature of an object can be measured using resistance by knowing the resistance at a given temperature and measuring the resistance at a new temperature. Using the formula ρ_t = ρ_0 * (1 + α * (T - T_0)), the new temperature can be calculated based on the change in resistivity.
What is the voltage drop across a 15-meter long copper wire with a cross-sectional radius of 3mm at 20 degrees Celsius?
-The voltage drop across the wire can be calculated using the formula V = I * R. With a current of 0.2 amps (200 milliamps) and a resistance of approximately 0.008913 ohms (calculated from the given resistivity, length, and area), the voltage drop is approximately 0.0017826 volts or 1.783 millivolts per 15 meters.
If a copper wire connected to a 12-volt battery conducts a current of 0.41 amps at a new temperature, is the new temperature higher or lower than 20 degrees Celsius?
-The new temperature is higher than 20 degrees Celsius. A decrease in current indicates an increase in resistance, which, for metals, occurs with an increase in temperature due to the positive temperature coefficient of resistivity.
How can you find the voltage drop per meter for the copper wire in the previous question?
-The voltage drop per meter can be found by dividing the total voltage drop by the length of the wire. For the given example, a voltage drop of approximately 1.783 millivolts over 15 meters results in a voltage drop of about 0.119 millivolts per meter.
Outlines
🔬 Understanding Resistance and Resistivity
This paragraph introduces the concepts of resistivity and resistance in wires. It explains how the resistance of a wire can be calculated using the formula R = ρ * L / A, where R is resistance, ρ is resistivity, L is the length of the wire, and A is the cross-sectional area. The discussion focuses on how resistance changes with the length and thickness of a wire, emphasizing that longer and thinner wires have higher resistance. The paragraph also compares the resistivity of different conductors, like silver and copper, and establishes that lower resistivity materials are better conductors of electricity.
🌡️ Impact of Temperature on Resistivity
This section delves into the relationship between temperature and resistivity, particularly for metals and semiconductors. It outlines the equation p_t = p_o * (1 + α * (T - T_0)), which shows how resistivity changes with temperature. The paragraph clarifies that for metals, resistivity increases with temperature, leading to higher resistance and less efficient electrical conduction. Conversely, semiconductors become more conductive as temperature rises. The practical application of this knowledge is also discussed, such as using resistance to measure temperature changes with digital thermometers.
🧮 Calculating Resistance of a Copper Wire
This paragraph presents a practical problem involving the calculation of resistance for a copper wire with a given length and cross-sectional radius. It provides the resistivity value at 20 degrees Celsius and the temperature coefficient. The problem is solved step by step, using the formula R = ρ * L / A, with the resistance calculated at different temperatures to demonstrate the effect of temperature on resistance. The paragraph also explains how to find the voltage drop across the wire at a specific temperature and current.
🔋 Voltage Drop in a Copper Wire
This section focuses on calculating the voltage drop across a wire when a current flows through it. It explains the formula for voltage drop, which is the product of current and resistance (V = I * R). Using the given current value and the calculated resistance, the paragraph determines the voltage drop per meter of the wire. It further illustrates how to calculate the voltage drop for different lengths of the wire, providing a clear understanding of how resistance and temperature affect voltage drop in electrical conductors.
🌡️ Determining Temperature Change from Current Variation
The final paragraph discusses a scenario where the temperature change is inferred from the variation in current through a wire. Given a copper wire connected to a battery and the change in current, the paragraph explains how to calculate the new temperature using the resistance at two different current values. It uses the relationship between resistivity, temperature, and resistance to solve for the new temperature, demonstrating the inverse relationship between temperature and conductivity in metals.
Mindmap
Keywords
💡Resistivity
💡Resistance
💡Conductors
💡Insulators
💡Semiconductors
💡Temperature Coefficient
💡Voltage Drop
💡Ohm's Law
💡Superconductors
💡Cross-Sectional Area
Highlights
The basic equation to calculate the resistance of a wire is derived from resistivity times the length of the wire divided by the area.
A longer wire has more resistance because the length (L) is in the numerator of the resistance calculation formula.
A thin wire has more resistance compared to a thick wire of the same length because the cross-sectional area affects the resistance inversely.
The resistivity (ρ) is a property of the material itself and indicates how well the material conducts electricity.
Silver is a better conductor than copper due to its lower resistivity value.
Materials with low resistivity are good electrical conductors, such as metals, while those with high resistivity are insulators.
Resistivity is a function of temperature and changes according to the equation ρ_t = ρ_o * (1 + α * (T - T_0)).
For metals, as the temperature increases, resistivity and resistance also increase, meaning metals conduct electricity better at lower temperatures.
Semiconductors have a negative temperature coefficient, meaning their resistivity decreases as temperature increases.
The relationship between temperature and resistivity can be used to measure the temperature of an object using resistance.
A 15-meter long copper wire with a 3mm radius has a resistance of 0.008913 ohms at 20 degrees Celsius and a resistivity of 1.68 * 10^-8.
The resistance of the copper wire at 50 degrees Celsius is 0.01073 ohms, calculated using the temperature coefficient and the initial resistance.
The voltage drop across the 15-meter copper wire at 20 degrees Celsius with 200 milliamps of current is 1.783 millivolts.
The voltage drop per meter for the copper wire is 0.119 millivolts, which can be used to calculate voltage drops at different lengths.
When a copper wire connected to a 12-volt battery conducts less current, it indicates a higher resistance and thus a higher temperature.
By calculating the resistance at different currents, it is possible to determine the new temperature of the copper wire based on its temperature coefficient.
The new temperature of the copper wire, when it conducts 0.41 amps instead of 0.45 amps, is found to be 34.34 degrees Celsius.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: