Antiderivatives
TLDRThe video lesson focuses on the concept of anti-derivatives, also known as integration. It explains that anti-derivatives are the reverse process of differentiation, aiming to find the original function from its derivative. The instructor introduces the integral symbol, the process of anti-differentiation, and the concept of an indefinite integral, which represents a family of functions due to the presence of a constant of integration. The video covers various integration rules, such as the power rule in reverse, the treatment of constants, and the integration of sums and differences. It also touches on integrating functions like e^x and the natural logarithm. The lesson demonstrates how to find particular anti-derivatives using given information, such as function values at specific points, to solve for the constant of integration. The instructor emphasizes the importance of verifying solutions by differentiating the results to check if they match the original derivative. The summary provides a clear and concise overview, inviting viewers to explore the intricacies of anti-derivatives and integration.
Takeaways
- 🔁 **Anti-derivatives**: An anti-derivative is the inverse operation of differentiation, allowing us to find the original function from its derivative.
- 🧠 **Anti-differentiation vs. Integration**: Anti-differentiation is also known as integration; both terms refer to the process of finding an antiderivative.
- 📈 **Indefinite Integrals**: When we integrate without specific limits, we deal with indefinite integrals, which represent a family of functions that differ by a constant (C).
- 📉 **Definite Integrals**: Unlike indefinite integrals, definite integrals have specific limits and provide a single numerical value.
- 🔍 **Finding the Original Function**: Given a derivative, we can find the original function by integrating and accounting for a constant (C) that could have been present.
- 📝 **Notation**: The integral symbol (∫) is used to denote the integration process, with the integrand being the function to be integrated and 'dx' indicating differentiation with respect to x.
- 🔢 **Power Rule**: When integrating a power of x, we use the power rule in reverse: add 1 to the exponent and divide by the new exponent, then add the constant of integration (C).
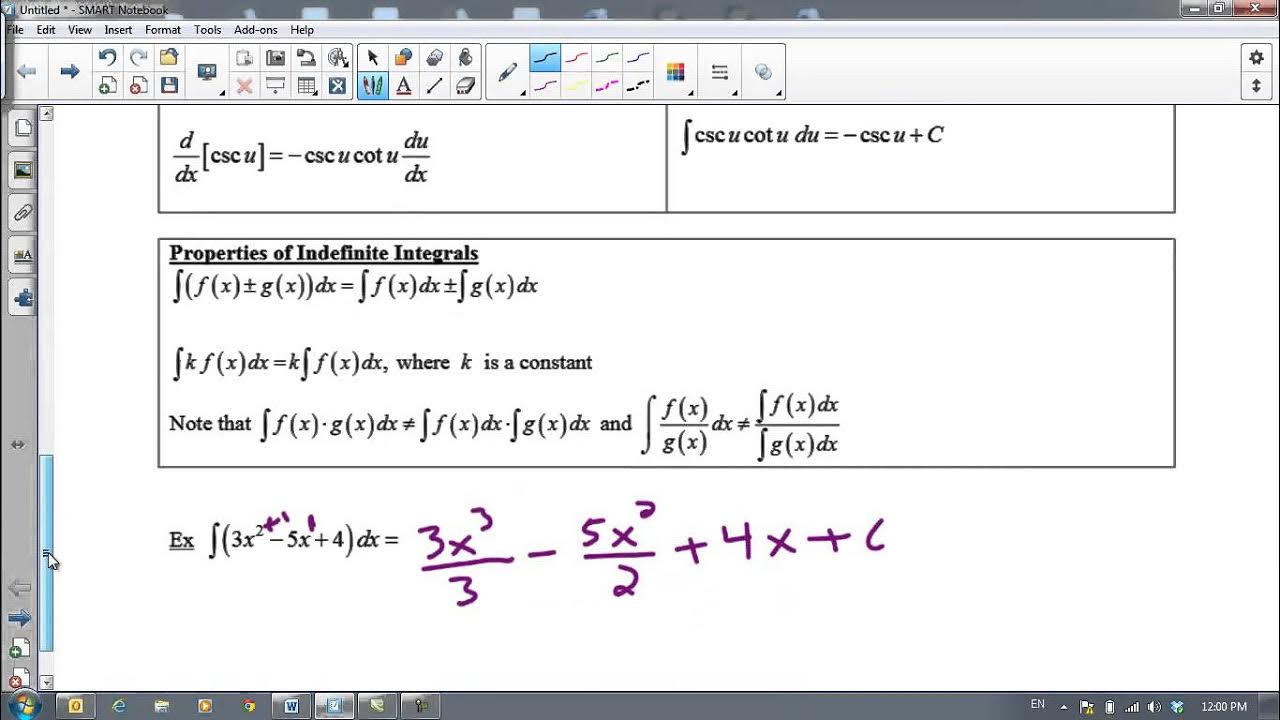
- ➕ **Constant Multiple Rule**: Integrating a constant times a function is equivalent to the constant times the integral of the function.
- ➖ **Sum/Difference Rule**: The integral of a sum or difference of functions is the sum or difference of their integrals, allowing us to integrate complex functions term by term.
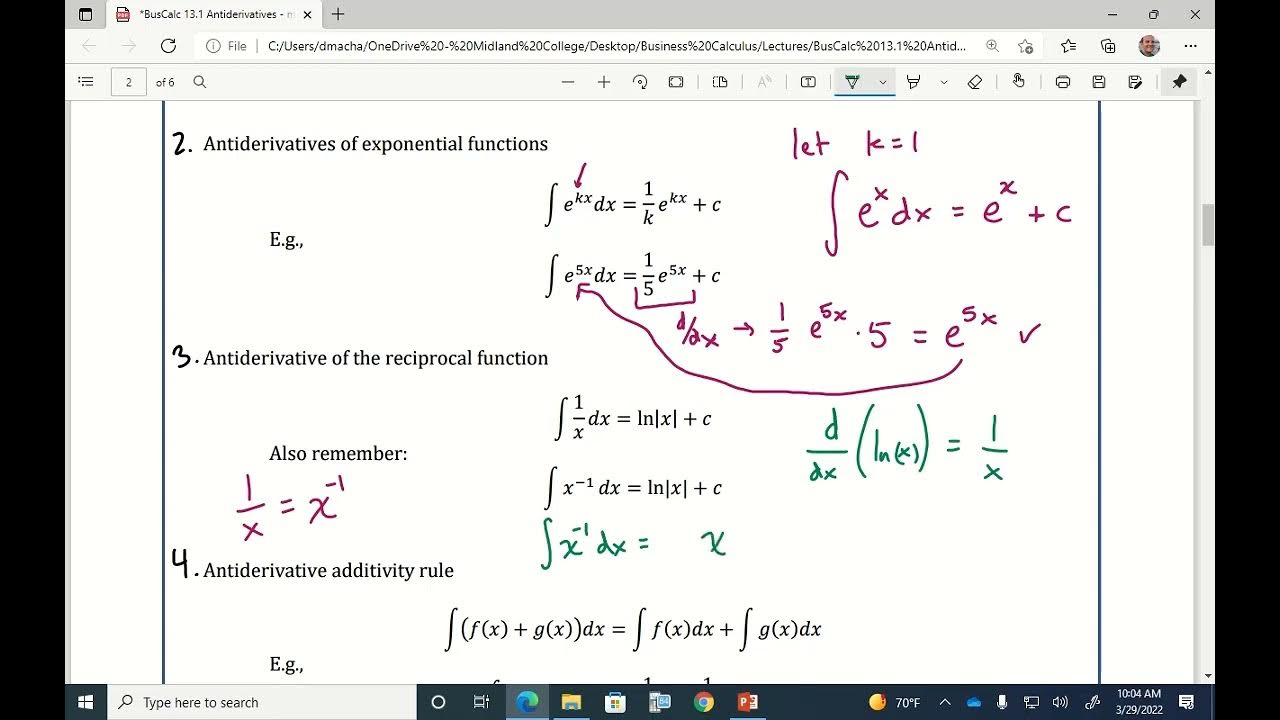
- 🛑 **Integration of Special Functions**: Functions like e^x and ln(x) have direct integration rules that relate back to their derivatives.
- 🔍 **Finding Particular Anti-derivatives**: By using additional information, such as the value of the function at a specific point, we can solve for the constant (C) and find a particular antiderivative.
Q & A
What is an anti-derivative?
-An anti-derivative is the opposite or the inverse of a derivative. It is the process of finding the original function given its derivative, essentially working backwards from differentiation.
What is another term for anti-differentiation?
-Anti-differentiation is also known as integration. The process of anti-differentiation is the same as the process of integration.
What is the symbol used to represent integration?
-The integral symbol ∫ is used to represent integration, indicating the process of finding an antiderivative.
Why is there a constant, often denoted as 'C', added when finding an antiderivative?
-The constant 'C' is added because when integrating, there could be a constant in the original function that disappears when taking the derivative. The constant 'C' accounts for any possible constant that could have been part of the original function.
What is the process called when you find a particular function from an indefinite integral by determining the value of the constant?
-The process is called finding a particular anti-derivative, and it involves using additional information, such as the value of the function at a specific point, to solve for the constant and determine the exact function.
What is the integral of a constant with respect to x?
-The integral of a constant with respect to x is the constant multiplied by x plus the constant of integration (C), resulting in a linear function.
What is the power rule for integration and how does it relate to the power rule for differentiation?
-The power rule for integration states that the integral of x to the power of n is (x to the power of n+1) divided by (n+1) plus the constant of integration (C). It is the reverse operation of the power rule for differentiation, which involves multiplying by the exponent and then subtracting 1 from the exponent.
How can you check your work when integrating?
-You can check your work by differentiating the result of your integration. If you've correctly found the antiderivative, differentiating it should take you back to the original function you were integrating.
What is the integral of the natural logarithm function with respect to x?
-The integral of 1/x with respect to x is the natural logarithm of the absolute value of x plus the constant of integration (C).
What does the term 'indefinite integral' refer to?
-An indefinite integral refers to a family of antiderivatives, which includes all possible original functions that could have produced a given derivative, differentiated with respect to a variable. It is called indefinite because the constant of integration (C) can be any real number.
How can you find a particular solution to an integration problem when given additional information, such as a point on the function?
-You can find a particular solution by substituting the given point into the indefinite integral to solve for the constant of integration (C), which then gives you a specific function rather than a family of functions.
Outlines
📚 Introduction to Anti-derivatives
The video begins with an introduction to anti-derivatives, explaining that they are the inverse process of differentiation. The lecturer emphasizes that anti-differentiation, also known as integration, involves finding the original function from its derivative, which is akin to reversing the process of differentiation. The concept of indefinite integrals is introduced, highlighting that they represent a family of functions due to the presence of a constant (C), which accounts for any constant term that might have been present in the original function.
📝 Understanding Anti-derivatives and Notation
The paragraph delves into the notation used for anti-derivatives, including the integral symbol, integrand, differential, and the constant of integration. The lecturer discusses the importance of including the constant of integration, C, in every integration to account for any constant that could have been part of the original function. The process of checking work by differentiating the result back to the original function is also covered.
🔢 Integration Rules: Constants and Power Rule
The video moves on to discuss the integration rules for constants and the power rule in reverse. It explains that the integral of a constant results in a linear term and that the power rule for integration involves adding one to the exponent and then dividing by the new exponent, followed by adding the constant of integration. The lecturer also demonstrates how to check the work by differentiating the integrated result.
🧮 Integration by Separation and Combining Terms
The paragraph covers the rule for integrating a sum or difference of multiple functions, which is done by integrating each term separately. The lecturer provides examples of integrating constants and polynomials, showing how to rewrite expressions and combine terms before integrating. The process of simplifying the integrated result is also demonstrated, with an emphasis on ensuring the constant of integration is included.
🔄 Applying Integration Rules for Polynomials and Rational Functions
The video continues with more complex examples, integrating quotients of polynomials and rational functions. The lecturer demonstrates how to rewrite and simplify expressions before applying the integration rules. The importance of converting improper fractions to a more manageable form is highlighted, and the use of natural logarithms in integration is introduced.
🔍 Finding Particular Anti-derivatives Using Given Values
The paragraph focuses on finding particular anti-derivatives by using given values of the function at specific points. The lecturer shows how to integrate to find the general form of the function and then use a point on the function to solve for the constant of integration, thereby finding the particular function. The process is demonstrated with examples that include finding the first and second derivatives to work backward to the original function.
📉 Verifying Integration with Differentiation
The final paragraph emphasizes the importance of verifying the integration process by differentiating the found anti-derivative to ensure it matches the original derivative. The lecturer reminds viewers that if unsure about their work, differentiating the result can serve as a check, and this process can be repeated for higher-order derivatives as well.
Mindmap
Keywords
💡Anti-derivative
💡Anti-differentiation
💡Indefinite integral
💡Definite integral
💡Integration
💡Constant of integration
💡Power rule
💡Derivative
💡Integral symbol
💡Differential
💡Particular anti-derivative
Highlights
An anti-derivative is the opposite or inverse of a derivative, representing the original function given its derivative.
Anti-differentiation is also known as integration, which is the process of finding an antiderivative.
The integral symbol indicates the process of anti-differentiation or integration, and the result is called the integral.
There are different types of integrals: indefinite integrals and definite integrals.
The integral of a function represents a family of antiderivatives, which includes a constant of integration, C.
The process of anti-differentiation requires accounting for a possible constant in the original function.
Capital F of x notation is used for the antiderivative of f of x, which when differentiated, returns the original function.
The integrand is the function being integrated, and the differential (DX) indicates the variable with respect to which the derivative was taken.
The constant of integration (C) is included in every integral to account for any possible constant in the original function.
The derivative of a constant times a function is the constant times the derivative of the function, a rule that also applies in reverse for integration.
Integration of a sum or difference of functions is the sum or difference of their individual integrals.
The integral of e to the x is simply e to the x plus a constant of integration, as it is its own derivative.
The integral of 1 over x is the natural log of the absolute value of x plus a constant, reflecting the derivative of the natural log function.
When integrating, it's important to avoid common mistakes such as omitting the constant of integration or misapplying power rules.
To find a particular antiderivative, additional information such as the value of the function at a specific point is required to solve for the constant C.
Verification of integration can be done by differentiating the result to see if it matches the original function or its derivatives.
Integration techniques include applying power rules in reverse, separating terms, and using logarithmic and exponential properties.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: