Math 11 - Section 4.5

Professor Monte

25 Apr 202035:20

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, Professor Monte delves into the concept of integration through the technique of substitution. He explains that substitution is essentially the reverse process of the chain rule in differentiation. The video provides a step-by-step guide on how to identify inside functions and apply substitution to simplify the integration process. Several examples are worked through, including those with limits of integration, to demonstrate the technique's application in solving integral calculus problems. The lecture concludes with an encouragement to practice these methods to ensure understanding and readiness for tests, with a promise of exploring applications of integration in economics in the next session.

Takeaways

📚 **Substitution in Integration**: The technique of substitution in integration is the reverse process of the chain rule in differentiation. It's used when an integral has an 'inside function' that requires the chain rule for its derivative.
⛓️ **Chain Rule Reversal**: When you encounter an integral that would require the chain rule for differentiation (like one involving an inner function), use substitution with 'u' to represent the inner function.
🔑 **Identifying Inside Functions**: Inside functions can often be recognized by their form, such as 'f(x) = (something)^n', roots like square roots, or functions like 'ln(something)', or 'e^(something)'.
📐 **Setting Up the Substitution**: Let 'u' be the inside function and find 'du/dx' to replace 'dx' in the integral, turning the integral into a function of 'u'.
🔄 **Integration Process**: After substitution, integrate with respect to 'u', and then convert back to the original variable by substituting 'u' back in.
🧮 **Checking the Solution**: To verify the integration, differentiate the result to see if it matches the original integrand.
📈 **Dealing with Exponential Functions**: When the inside function is an exponential, like 'e^(ax)', set 'u' to the exponent 'ax' and adjust the integral accordingly.
📉 **Logarithmic Integration**: For logarithmic functions, such as 'ln(x)', set 'u' equal to the argument of the logarithm and use 'du/dx' to transform the integral.
🔢 **Numerical Evaluation**: When limits of integration are provided, apply the substitution, find the antiderivative, and then use the limits to find a numerical answer.
🏁 **Fundamental Theorem of Calculus**: Use the fundamental theorem of calculus to evaluate definite integrals by finding antiderivatives and applying the limits of integration.
⚖️ **Consumer and Producer Surplus**: The lecture concludes with a mention of an application of integration in economics, specifically in the context of consumer and producer surplus, which will be covered in a subsequent lecture.

Q & A

What is the main topic of the lecture?
-The main topic of the lecture is integration techniques, specifically focusing on the method of substitution.
How is the substitution method related to the chain rule in differentiation?
-The substitution method is the reverse process of the chain rule in differentiation. It is used when dealing with integrals that have an 'inside function', similar to how the chain rule is applied when differentiating such functions.
What is typically represented by the letter 'U' in the context of substitution?
-In the context of substitution, the letter 'U' is typically used to represent the inside function of the integral.
What is an example of an inside function in integration?
-Examples of inside functions include expressions like f(x) = (something)^a, where 'something' is inside the parentheses, or functions involving roots like a square root or cube root, or exponential functions like e^(something).
How does the lecturer demonstrate the process of substitution in the first example?
-The lecturer demonstrates the process by letting u = x^2 - 7, then taking the derivative du/dx = 2x, and substituting this into the integral to simplify the expression before integrating.
What is the purpose of checking the derivative after finding the integral?
-Checking the derivative after finding the integral serves as a verification step to ensure that the antiderivative, or integral, has been calculated correctly.
What is the role of the constant 'C' in the antiderivative?
-The constant 'C' is the constant of integration, which is added to the integrated result to account for any constant term that may have been present in the original antiderivative.
How does the lecturer handle the process of substitution when limits of integration are involved?
-When limits of integration are involved, the lecturer uses the substitution method to simplify the integral and then applies the fundamental theorem of calculus by plugging in the limits of integration to find a specific numerical value.
What is the lecturer's advice for students who find the concept of substitution confusing?
-The lecturer advises students to practice by going through as many steps as they can with the original problem, pausing to understand each step, and if they get stuck, to figure out what the next step should have been.
Why does the lecturer emphasize the importance of correctly substituting back (re-substitution) after integrating in terms of 'U'?
-Correctly substituting back is crucial because it transforms the integrated expression back into terms of the original variable, which is necessary for providing the final answer in the context of the original problem.
What is the final example's integral that the lecturer solves in the script?
-The final example's integral that the lecturer solves is ∫(x * (x^2 - 1)^7) dx from 1 to 2, which involves identifying x^2 - 1 as 'U', integrating, and then finding the value using the limits of integration.

Outlines

00:00

📚 Introduction to Integration Techniques

Professor Monte introduces the topic of integration techniques, specifically focusing on the method of substitution. He explains that substitution is the reverse process of the chain rule in differentiation. The lecture aims to teach how to handle integrals with inner functions by substituting them with a new variable, typically represented by 'u'. The professor also reminds the audience of the concept of inner functions using examples such as f(x), H(x), and e^(something), where 'something' is the inner function.

05:03

🧮 Substitution with Leibnitz Notation

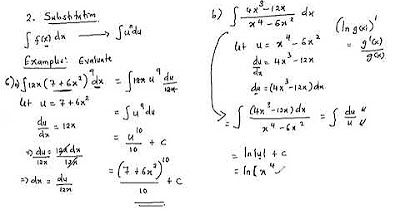
The professor demonstrates the application of substitution in integration using Leibnitz notation. He takes the audience through the process of substituting 'u' for an inner function, taking the derivative of 'u' with respect to 'x', and then integrating with respect to 'u'. An example is given where the integral of (x^2 - 7)^6 * 2x is solved by letting u = x^2 - 7, and then integrating u^6 with respect to u. The solution is checked by differentiating the result to ensure it matches the original integrand.

10:04

🔍 More Examples of Substitution

The professor continues with more examples of integration using substitution. He covers integrals involving t^5 - 3, the natural logarithm of x (ln x), and e^(7x). In each case, he identifies the inner function, performs the substitution, and integrates with respect to the new variable 'u'. The process involves simplifying the integral, performing the substitution, integrating, and then substituting back to express the final answer in terms of the original variable.

15:05

📉 Integration with Limits of Integration

The lecture moves on to solving integrals with limits of integration. The professor emphasizes the use of the fundamental theorem of calculus to find the definite integral by substituting the limits into the antiderivative. Examples include integrating 3x^2 * e^(x^3) from 0 to 1 and x(x^2 - 1)^7 from 1 to 2. The professor shows how to perform the substitution, integrate, and then apply the limits to find a numerical value for the integral.

20:06

🔢 Finalizing Integration by Substitution

In the final part of the lecture, the professor summarizes the technique of integration by substitution. He reiterates that this method is used when an integral suggests the need for the chain rule in differentiation. The professor advises students to practice multiple examples to solidify their understanding and to check their work by differentiating the result to ensure it matches the original integrand. He also mentions that the next lecture will cover an application of integration in economics, specifically producer and consumer surplus.

Mindmap

Keywords

💡Integration

Integration is a mathematical process of finding an antiderivative, which is a function whose derivative is the given function. In the context of the video, integration is a technique used to solve complex calculus problems, particularly when dealing with functions that can be expressed as a composition of simpler functions.

💡Substitution

Substitution is a method in calculus used to transform an integral into a more manageable form. It is especially useful when the integral resembles the reverse of a differentiation process, such as when an 'inside function' is present. In the video, substitution is the primary technique discussed for solving integrals, and it is likened to the reverse of the chain rule in differentiation.

💡Chain Rule

The chain rule is a fundamental theorem in calculus for differentiating composite functions. It states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function. In the video, the chain rule is mentioned as a contrasting concept to help understand when to apply substitution in integration.

💡Inside Function

An inside function refers to the part of a composite function that is affected by the outer function. In the context of the video, identifying the inside function is crucial for applying the substitution method correctly. For example, if the integral is of the form ∫ f(g(x)) g'(x) dx, then g(x) is considered the inside function.

💡Derivative

A derivative in calculus represents the rate of change of a function with respect to its variable. It is the fundamental concept that the process of integration is designed to reverse. In the video, the process of taking derivatives is discussed in relation to the substitution method, particularly when identifying the inside function.

💡Antiderivative

An antiderivative, also known as an indefinite integral, is a function whose derivative is equal to the original function. Finding antiderivatives is the primary goal of integration. The video focuses on using substitution to find antiderivatives of complex functions.

💡Leibniz Notation

Leibniz notation is a way of representing derivatives and integrals in calculus, named after the mathematician Gottfried Wilhelm Leibniz. It uses the symbols 'dx' to denote an infinitesimal change in the variable 'x'. In the video, Leibniz notation is used to illustrate the process of taking derivatives and how it relates to the substitution method in integration.

💡Limits of Integration

Limits of integration are values that specify the range over which an integral is computed. They are used in definite integrals to provide a specific numerical value. In the video, the concept is demonstrated by applying substitution within definite integrals to find exact values.

💡Producer Surplus and Consumer Surplus

Producer surplus and consumer surplus are economic terms that refer to the benefit derived by producers and consumers, respectively, from participating in a market. Although not the main focus of the video, these terms are mentioned as an application of integration that will be covered in a subsequent section.

💡Fundamental Theorem of Calculus

The Fundamental Theorem of Calculus is a theorem that links the concept of the definite integral to the antiderivative, stating that the definite integral can be computed by finding an antiderivative and subtracting the value of the antiderivative at the lower limit of integration from its value at the upper limit. In the video, this theorem is alluded to when discussing how to find a numeric value for a definite integral using substitution.

Highlights

Professor Monte introduces the concept of integration by substitution, which is the reverse process of the chain rule in differentiation.

Substitution is used when dealing with integrals that have an 'inside function', which is the part of the function that would be affected by the chain rule during differentiation.

The letter 'u' is commonly used to represent the inside function during the substitution process.

Examples of inside functions include expressions within radicals, logarithms, and exponential powers.

The process of substitution involves setting the inside function equal to 'u', taking the derivative of 'u', and then rewriting the integral in terms of 'u'.

After substitution, the integral is simplified by integrating with respect to 'u' and then converting back to the original variable.

The technique of substitution can be checked for correctness by differentiating the result and comparing it to the original integrand.

Integration by substitution is particularly useful for integrals that do not have a direct antiderivative or are complex to integrate directly.

The lecture demonstrates several examples of substitution, illustrating the process step by step.

When applying limits of integration after substitution, it is crucial to re-substitute the original variable back into the integral.

The Fundamental Theorem of Calculus is used to find the numeric value of definite integrals after applying substitution.

The lecture emphasizes the importance of practice and reviewing examples to solidify the understanding of the substitution method.

Professor Monte provides a method to check the solution by differentiating the antiderivative and comparing it with the original integrand.

The use of substitution is demonstrated in integrals involving exponential functions, logarithms, and polynomials.

The process of substitution is shown to simplify complex integrals, making them easier to solve.

The lecture concludes with an application of integration to economic concepts such as producer and consumer surplus.

Throughout the lecture, the importance of understanding the underlying principles of substitution is emphasized over memorization of formulas.

The lecture provides a comprehensive overview of the technique of integration by substitution, suitable for students preparing for exams.

Transcripts

Browse More Related Video

Integration by Substitution

Indefinite Integration (part IV)

U Substitution!

Math 1325 Lecture 12 2

MATH 1325 Lecture 12 3 Integrals of Exponents and Logarithms

Integration using substitution method

Related Tags

Integration Techniques Substitution Method Chain Rule Professor Monte Mathematical Analysis Inside Functions Derivatives Integral Calculus Lectures Educational Content