Kirchhoff's Voltage Law (KVL) Explained
TLDRThis video script offers a comprehensive explanation of Kirchhoff's Voltage Law, a fundamental concept in electrical circuit analysis. It emphasizes the importance of understanding current direction and voltage drops across resistors, and demonstrates how to apply the law to calculate voltages and current in various circuit configurations, including those with multiple voltage sources and different components. The lesson concludes with a promise to cover Kirchhoff's Current Law in a future video, ensuring viewers are equipped with the necessary tools for advanced circuit analysis.
Takeaways
- 📚 Kirchhoff's Laws are fundamental for analyzing electrical circuits, consisting of two laws: current and voltage.
- 🧭 To determine the direction of current in a circuit, start from the positive pole and end at the negative pole; if unsure, assume a direction and confirm with the calculated current's sign.
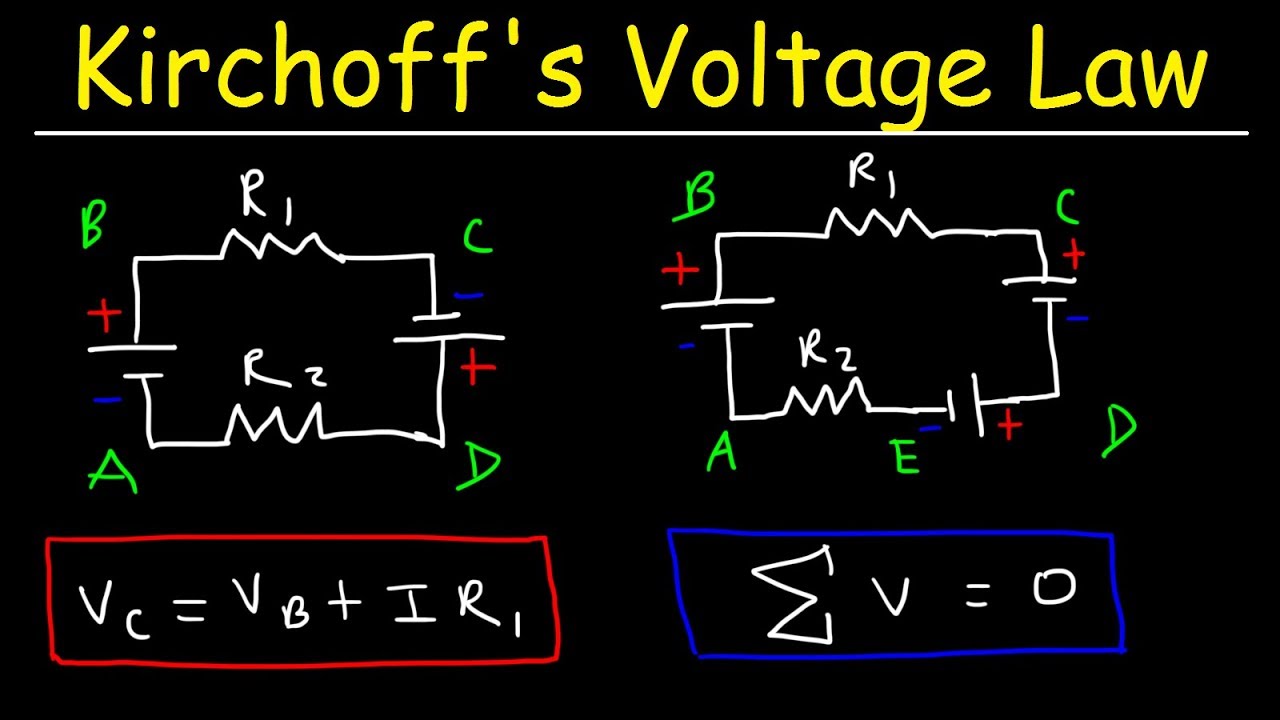
- 🔋 Kirchhoff's Voltage Law states that the sum of voltages around any closed loop in a circuit is equal to zero, accounting for both produced and consumed voltages.
- 🔄 When applying Kirchhoff's Voltage Law, consider the direction of current and assign positive or negative signs to the voltages across components accordingly.
- 📈 The voltage drop across resistors is proportional to their resistance values and can be calculated using Ohm's Law (V = I.R).
- 🔌 In circuits with multiple voltage sources, the algebraic sum of the source and resistor voltages must equal zero when applying Kirchhoff's Voltage Law.
- ⚙️ Kirchhoff's Laws are applicable to complex circuits with various components, such as diodes and transistors.
- 🔮 When a negative current value is obtained, it indicates that the assumed direction of current is opposite to the actual direction.
- 🌐 The sum of consumed voltages (across resistors) should equal the generated voltage (source voltage) in a circuit.
- 📝 Practice problem-solving using Kirchhoff's Voltage Law to find unknown values in circuits, such as current and voltage across components.
- 🎓 The next lesson will cover Kirchhoff's Current Law, further enhancing the understanding of circuit analysis.
Q & A
What are Kirchhoff's Laws and why are they important in analyzing electrical circuits?
-Kirchhoff's Laws are fundamental principles used in the analysis of electrical circuits, consisting of Kirchhoff's Current Law and Kirchhoff's Voltage Law. They are important because they provide a systematic approach to understanding the behavior of electrical circuits, allowing us to calculate unknown quantities such as current and voltage across components.
What does Kirchhoff's Current Law state?
-Kirchhoff's Current Law, also known as Kirchhoff's First Law, states that the total current entering a junction (node) in a circuit is equal to the total current leaving the junction. This is based on the principle of conservation of charge, implying that charge can neither be created nor destroyed in a circuit.
How can we determine the direction of current in a circuit?
-The direction of current in a circuit can often be visually identified, flowing from the positive (+) pole to the negative (–) pole of a power source. In complex circuits where the direction is not clear, a conventional current direction can be assumed. The actual direction can be confirmed by the sign of the current value calculated; a positive value confirms the assumed direction, while a negative value indicates the opposite direction.
What is the Kirchhoff's Voltage Law and how does it relate to the consumed and produced voltages in a circuit?
-Kirchhoff's Voltage Law, also known as Kirchhoff's Second Law, states that the algebraic sum of the voltages around any closed loop or mesh in a network is zero. This means that the total voltage produced by the sources in a circuit is equal to the total voltage consumed by the elements (like resistors) within the circuit.
How can we apply Kirchhoff's Voltage Law to find the voltage across resistors in a circuit?
-By applying Kirchhoff's Voltage Law, we can write equations for each closed loop in the circuit, considering the voltage drops across resistors (V = I * R) and the voltage supplied by the sources. Solving these equations allows us to find the unknown voltages across the resistors and the current flowing through the circuit.
What happens when the calculated current value is negative according to Kirchhoff's Laws?
-A negative current value indicates that the assumed direction of current flow is opposite to the actual direction. This means that the current is flowing in the reverse direction of what was initially guessed, and the actual direction should be considered as the opposite for accurate analysis of the circuit.
How are the voltages across resistors related to their resistance values?
-In a circuit, the voltage across a resistor is directly proportional to its resistance value when the same current flows through them. This relationship is derived from Ohm's Law (V = I * R), where a higher resistance will result in a larger voltage drop across that resistor for a given current.
Can Kirchhoff's Voltage Law be applied to circuits with non-resistive components?
-Yes, Kirchhoff's Voltage Law can be applied to circuits with non-resistive components like diodes, capacitors, and transistors. The law is a general principle that states the sum of voltages around any loop must be zero, and it can be adapted to include the voltage characteristics of these components in the analysis.
What is the significance of the example with two voltage sources in the script?
-The example with two voltage sources demonstrates the application of Kirchhoff's Voltage Law in more complex circuits with multiple power sources. It shows how to determine the actual direction of current flow and how the voltages across resistors and the generated voltage from the sources relate to each other, reinforcing the principle that the sum of consumed and produced voltages must be equal.
How does the script's explanation of Kirchhoff's Voltage Law contribute to understanding circuit analysis?
-The script provides a clear and detailed explanation of Kirchhoff's Voltage Law, using practical examples to illustrate how the law can be applied to analyze and solve for unknown quantities in electrical circuits. This understanding is crucial for anyone studying or working with electronics and electrical engineering.
What will be the topic of the next lesson after Kirchhoff's Voltage Law?
-The next lesson will focus on Kirchhoff's Current Law, which is the other fundamental principle of Kirchhoff's Laws used in circuit analysis. This law will further enhance the understanding of how to analyze and calculate currents in various network configurations.
Outlines
📚 Introduction to Kirchhoff's Laws
This paragraph introduces Kirchhoff's Laws, emphasizing their importance in analyzing electrical circuits. It outlines the two fundamental laws: the current law and the voltage law. The video focuses on explaining Kirchhoff's Voltage Law, which is based on the principle that the algebraic sum of all voltages in a circuit is zero. The explanation includes determining the direction of current, assigning voltage values to resistors, and applying the law to find the consumed voltages. An example is provided to illustrate how to calculate the current and voltage across resistors, demonstrating that the sum of consumed voltages equals the source voltage.
🔍 Application of Kirchhoff's Voltage Law in Circuits with Multiple Voltage Sources
This paragraph delves into the application of Kirchhoff's Voltage Law in more complex circuits that include multiple voltage sources. It explains how to handle situations where the current direction is not immediately clear by making assumptions and using the law to verify them. The paragraph provides a detailed example with two voltage sources, VA and VB, and explains how to calculate the voltage across resistors and the main current value. It highlights the importance of understanding the relationship between the generated and consumed voltages and how the voltage across resistors is proportional to their resistance values. The paragraph concludes by mentioning that Kirchhoff's Voltage Law can be applied to various circuit components, not just resistors.
Mindmap
Keywords
💡Kirchhoff's Laws
💡Current Direction
💡Voltage
💡Resistors
💡Circuit Analysis
💡Ohm's Law
💡Example Circuits
💡Voltage Sources
💡Kirchhoff Voltage Law Application
💡Proportional Voltages
💡Complex Circuits
Highlights
Introduction to Kirchhoff's Laws as fundamental for analyzing electrical circuits.
Explanation of Kirchhoff's Voltage Law, one of the two fundamental laws.
Importance of understanding the direction of current in a circuit, even when it's not clearly visible.
Method to estimate the direction of current if it's not directly observable.
Procedure to label voltage across resistors and the role of resistors in consuming voltage.
Formula representation of Kirchhoff's Voltage Law and its implications.
The concept that the sum of all voltages in a circuit equals zero.
Illustration of Kirchhoff's Voltage Law through a practical example involving resistors.
Explanation of how voltage values across resistors are determined using Ohm's Law.
Demonstration that voltages across resistors are proportional to their resistance values.
Application of Kirchhoff's Voltage Law in circuits with multiple voltage sources.
Procedure to find the current direction when it's initially unknown.
How to apply Kirchhoff's Voltage Law in complex circuits with different components.
Example of applying the law in a circuit with a diode and resistor.
Detailed application of the law in a BJT transistor circuit with two meshes.
Conclusion on the fundamental nature of Kirchhoff's Voltage Law for circuit analysis.
Anticipation of the next lesson on Kirchhoff's Current Law.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: