Kirchhoff's Law, Junction & Loop Rule, Ohm's Law - KCl & KVl Circuit Analysis - Physics
TLDRThis video tutorial explains the application of Kirchhoff's Junction and Loop Rules for calculating currents in complex circuits. It provides a step-by-step walkthrough of how to use these rules to solve circuit problems, including determining the direction of current flow and calculating voltage drops across resistors. The video also emphasizes the importance of understanding the relationship between current flow, potential differences, and resistor values to successfully analyze and solve circuit problems.
Takeaways
- 📚 Kirchhoff's Junction Rule states that the total current entering a junction equals the total current leaving the junction, which is key in analyzing complex circuits.
- 🔄 Kirchhoff's Voltage Law, or Loop Rule, asserts that the sum of all voltages around a closed loop in a circuit must equal zero, crucial for determining the potential differences and currents in loops.
- 🧠 Understanding the direction of current flow and potential differences (voltage drops and lifts) is essential for applying the loop rule correctly in calculations.
- 🔌 To solve circuits with multiple loops and unknown currents, establishing a system of equations based on Kirchhoff's rules allows for the determination of unknown current variables.
- 🤔 When dealing with resistors in series and parallel, the current through each resistor can be different, and the voltage drop across each resistor is given by the product of the current and resistance.
- 🔄 For a circuit with a battery, the potential difference across the battery terminals defines the direction of the electromotive force (EMF) and the potential differences in the circuit.
- 💡 When calculating potentials in a circuit, it's helpful to pick a reference point (usually ground) and understand that moving from high to low potential involves a voltage drop, and vice versa.
- 📈 To solve for multiple unknowns in a circuit, techniques such as elimination or substitution can be used to reduce the system of equations to a more manageable form.
- 🛠️ When solving complex circuit problems, it's beneficial to redraw the circuit with the calculated currents and potentials to visually confirm that the solution makes sense and all the equations balance.
- 🔧 In circuits with multiple batteries, the overall EMF and current direction are determined by the combined effect of the individual battery EMFs.
- 📊 Systematic problem-solving, including checking work and ensuring that all calculated values are consistent with the laws of physics, is critical in circuit analysis.
Q & A
What are Kirchhoff's two main rules for analyzing circuits?
-Kirchhoff's two main rules are the Current Law (Junction Rule) and the Voltage Law (Loop Rule). The Current Law states that the total current entering a junction equals the total current leaving the junction. The Voltage Law states that the sum of all voltages around a closed loop in a circuit must equal zero.
How does the direction of current flow affect the calculation of voltage drops and voltage lifts?
-The direction of current flow determines whether a component in the circuit will be associated with a voltage drop or a voltage lift. If you move in the direction of the current and it's going from high potential to low potential, it's associated with a voltage drop. Conversely, if you move against the direction of the current (from low potential to high potential), it's associated with a voltage lift.
What is the significance of using loop and junction rules in solving complex circuits?
-Using Kirchhoff's loop and junction rules is crucial in solving complex circuits as they provide a systematic approach to analyzing the currents and voltages in the circuit. These rules help in setting up equations that can be solved to find the unknown currents flowing through each component and the potential at different points in the circuit.
How can you determine the direction of the current in a circuit with multiple power sources?
-In a circuit with multiple power sources, the overall direction of the current is determined by the relative strengths of the voltages. The current will generally flow from regions of higher potential (created by higher voltage batteries) to regions of lower potential (created by lower voltage batteries). The net direction can be predicted by comparing the combined effect of the voltages.
What is the relationship between current, resistance, and voltage drop in a resistor?
-The voltage drop across a resistor is directly proportional to the current flowing through it and its resistance. This relationship is described by Ohm's Law, which states that the voltage (V) across a resistor is equal to the product of the current (I) flowing through it and its resistance (R), expressed as V = I * R.
How can you calculate the electric potential at any point in a circuit given a reference potential?
-To calculate the electric potential at any point in a circuit, you start with a reference potential (usually ground at 0 volts). As you move through the circuit, you add up the voltage lifts (going from low potential to high potential) and subtract the voltage drops (going from high potential to low potential). This cumulative sum gives you the electric potential at any point in the circuit relative to the reference point.
What is the importance of checking your work when solving circuit problems?
-Checking your work is important in circuit problems to ensure accuracy and to catch any mistakes that might have been made during the problem-solving process. It can help verify that the calculated currents and potentials are consistent and logical within the context of the circuit. This practice helps to avoid the frustration of long problems becoming unsolvable due to a single error.
How can you simplify the process of solving a circuit with multiple loops and junctions?
-One way to simplify the process is by reducing the number of variables and equations needed. For instance, if a junction has multiple currents flowing into or out of it, you can use Kirchhoff's Current Law to express one of the currents in terms of the others. This reduces the number of separate currents you need to track and solve for, making the problem more manageable.
What happens when you encounter a negative value for current in circuit analysis?
-A negative value for current indicates that the assumed direction of the current is opposite to the actual direction of flow. In this case, you should reverse the direction of the current in your analysis. This changes the sign of the current, allowing the analysis to proceed correctly with the proper direction of current flow.
What is the role of voltage sources in determining the direction of current in a circuit?
-Voltage sources play a crucial role in determining the direction of current in a circuit. They create a potential difference that drives the current through the circuit. The current will flow from the positive terminal to the negative terminal of a voltage source. The strength of the voltage source influences the overall direction of the current in the presence of multiple sources.
In the context of the video, how does the process of solving for currents and potentials in a complex circuit help in understanding circuit behavior?
-Solving for currents and potentials provides a detailed understanding of how a circuit operates. It allows us to predict the behavior of complex circuits, such as how the current will flow through different branches, the voltage drops across resistors, and the potential at various points. This understanding is crucial for circuit design, troubleshooting, and optimization.
Outlines
📝 Introduction to Kirchhoff's Rules
This paragraph introduces the concept of using Kirchhoff's junction and loop rules to calculate currents in complex circuits. A problem involving resistors in series and parallel is presented, with the goal of calculating the current flowing through each resistor. The paragraph sets the stage for applying Kirchhoff's laws to solve for unknown currents in a given electrical circuit.
🔍 Applying Kirchhoff's Junction Rule
The second paragraph delves into the application of Kirchhoff's junction rule, which states that the current entering a junction must equal the sum of currents leaving the junction. The explanation includes a step-by-step walkthrough of how to set up and solve an equation using this rule, highlighting the importance of understanding where currents enter and leave in order to balance the equation correctly.
🌡️ Utilizing Kirchhoff's Voltage Law
This section explains Kirchhoff's voltage law, emphasizing the significance of understanding the direction of current flow and how it relates to voltage drops and lifts around a circuit loop. The explanation clarifies how to determine the polarity of voltage contributions based on the current direction, which is crucial for accurately applying the loop rule in calculations.
🔧 Solving the Circuit Problem
The paragraph focuses on solving the initial circuit problem by applying both Kirchhoff's rules. It provides a detailed explanation of how to use the loop rule to set up equations around the circuit, considering the voltage drops across resistors and the polarity of battery voltages. The process involves creating a system of equations that can be solved to find the unknown currents in the circuit.
📊 Analyzing the Circuit Analysis
This part of the script involves a thorough analysis of the circuit to ensure that the calculated currents and voltages make sense. The video script includes a step-by-step verification of the calculated currents and potential differences across various components in the circuit. It emphasizes the importance of checking the work to confirm the accuracy of the solutions.
🔄 Addressing a Second Circuit Problem
The paragraph introduces a new circuit problem with multiple batteries and resistors, aiming to calculate the current flowing through the circuit. It discusses the importance of predicting the direction of currents based on the voltage of the batteries and provides a method for simplifying the problem by reducing the number of variables involved.
📐 Working Through a Complex Circuit
This section presents a complex circuit with multiple loops and batteries, guiding the viewer through the process of calculating the current flowing through each branch. The explanation involves setting up and solving a system of equations based on Kirchhoff's rules, while also discussing the direction of currents and the potential at various points in the circuit.
🔍 Solving the Final Circuit Problem
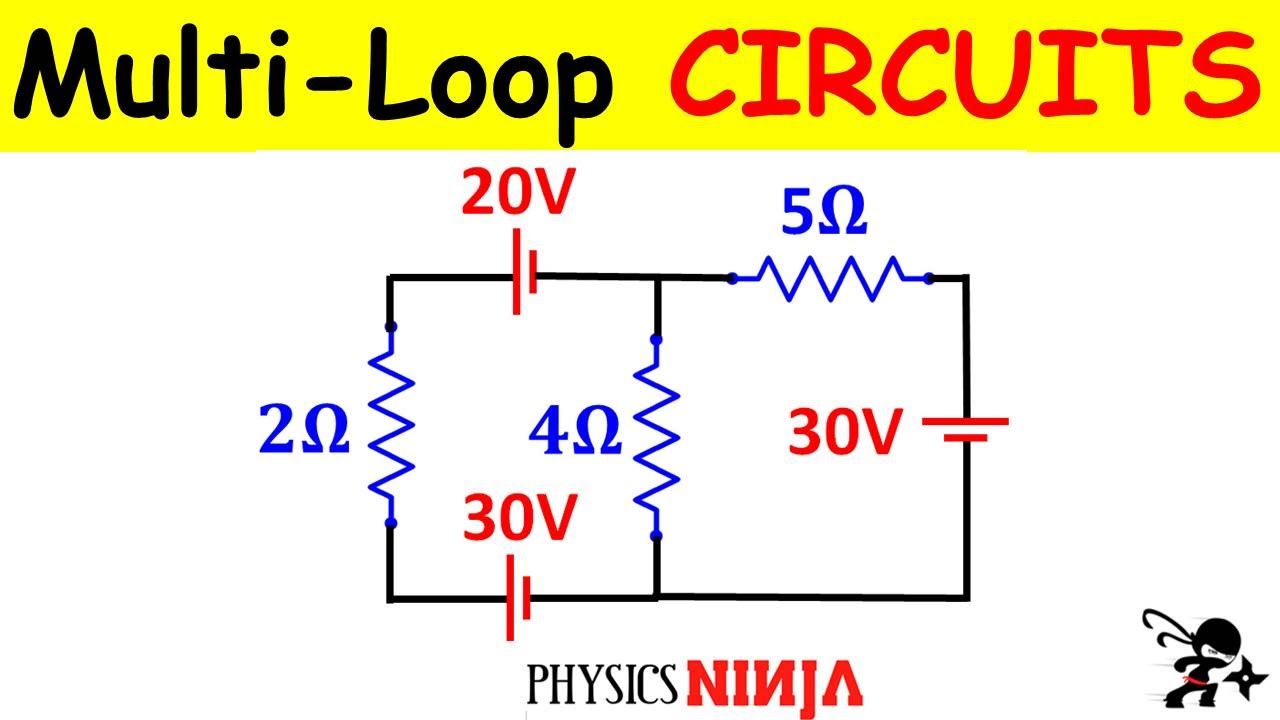
The final paragraph of the script involves solving a more intricate circuit problem with multiple resistors and batteries. It outlines the process of defining currents through various resistors and setting up a system of equations to solve for the unknown currents. The paragraph emphasizes the importance of understanding the relationships between the currents and the application of Kirchhoff's rules to find the solution.
🎓 Conclusion and Final Problem Solving
The conclusion of the video script reiterates the process of using Kirchhoff's junction and loop rules to calculate currents in a circuit and determine the electric potential at any point. It presents a final, more complex problem for the viewer to attempt, summarizing the steps and methods used throughout the video to analyze and solve electrical circuit problems.
Mindmap
Keywords
💡Kirchhoff's Junction Rule
💡Kirchhoff's Voltage Law
💡Resistors
💡Ohm's Law
💡Current
💡Voltage
💡Loop Rule
💡Potential
💡Series and Parallel Circuits
💡Circuit Analysis
Highlights
Introduction to Kirchhoff's Junction and Loop Rules for calculating current in complex circuits.
Explanation of a series-parallel resistor circuit with values and the application of Kirchhoff's rules.
Derivation and use of the first Kirchhoff's equation (Junction Rule) for the given circuit.
Application of Kirchhoff's Voltage Law (Loop Rule) in analyzing the circuit.
Determination of positive and negative voltage contributions based on current direction.
Explanation of how to handle resistors in series and parallel within the circuit analysis.
Step-by-step calculation of currents through each resistor using Kirchhoff's rules.
Verification of the calculated currents using Kirchhoff's laws and circuit analysis.
Introduction of a second, more complex circuit problem involving multiple batteries and resistors.
Prediction of current flow direction based on battery voltages and the use of elimination method to simplify the problem.
Detailed breakdown of loop analysis for the complex circuit, including voltage lifts and drops.
Solving for the currents in the complex circuit and verifying the results with potential calculations.
Final problem involving multiple resistors and batteries, with a step-by-step approach to finding the currents in each branch.
Use of system of equations to solve for unknown currents in the presence of multiple loops and junctions.
Calculation of electric potential at various points in the circuit based on reference point and current flow.
Comprehensive analysis and verification of the electric potential and current calculations in the complex circuit.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: