AP Physics Workbook 6.K Mass and Period of Mass Spring System

Mr.S ClassRoom
15 Apr 202013:00
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses a physics problem involving a mass-spring system and the concept of simple harmonic motion. It explains how the period of oscillation changes when mass is added to the system at a constant rate. The video also delves into the concept of mechanical energy and its conservation in elastic collisions, and how the introduction of sand (or a damping medium) leads to a decrease in the system's energy over time, resulting in damped oscillations. This is visually demonstrated and further explained through the concept of work and energy transfer, highlighting the real-world application in car suspensions.

Takeaways
  • 📚 The topic is AP Physics, focusing on Unit 6: Simple Harmonic Motion, specifically section 6.K on mass and period of a mass-spring system.
  • 🔢 Given data: mass of the cart (M) is 0.5 kg, and mass is entering the cart at a rate of 0.1 kg/s.
  • ⏱ The period of oscillation (T) is given by the formula T = 2π√(M/K), and the challenge is to find the time when the period becomes 2T.
  • 🎢 To achieve a period of 2T, the mass (M) must be doubled, as per the equation, requiring the system's mass to increase from 0.5 kg to 2 kg.
  • 📈 The mass increase is calculated by the difference in mass (final - initial), which is 2 kg - 0.5 kg = 1.5 kg.
  • 🕰️ The time required for the mass to increase by 1.5 kg is determined by setting up a proportion based on the mass gain rate, resulting in 150 seconds.
  • 🌐 The script also discusses the concept of mechanical energy in a system, noting that it decreases over time due to the addition of sand (or another mass).
  • 🏎️ The energy loss in the system is likened to the working principle of car shock absorbers, which dissipate energy to reduce oscillation.
  • 📉 As the mass continues to increase, the amplitude of the simple harmonic motion decreases over time due to underdamping.
  • 📊 The graphical representation of the motion shows a damping effect where the oscillation amplitude reduces with each successive cycle.
  • 🤔 The script encourages understanding of why simple harmonic motion loses energy over time as mass is added to the system.
Q & A

  • What is the topic of the video?

    -The topic of the video is about simple harmonic motion in the context of a mass-spring system, specifically focusing on how the mass of an object affects the period of oscillation.

  • What are the given values for the mass of the cart and the rate at which mass is entering the cart?

    -The given value for the mass of the cart is M = 0.5 kilograms. The rate at which mass is entering the cart is 0.1 kilograms per second.

  • What is the formula for the period of a mass-spring system?

    -The formula for the period of a mass-spring system is T = 2π√(M/K), where M is the mass and K is the spring constant.

  • How does the period of oscillation change when the mass of the system changes?

    -The period of oscillation is directly proportional to the square root of the mass. If the mass doubles, the period will also double.

  • What is the initial and final mass of the system in the example given?

    -The initial mass of the system is 0.5 kilograms. After the mass increases, the final mass becomes 2 kilograms.

  • How much time is required for the mass to increase by 1.5 kilograms?

    -The time required for the mass to increase by 1.5 kilograms is 150 seconds, calculated by setting up a proportion with the given rate of mass increase.

  • Why does the mechanical energy of the system decrease over time?

    -The mechanical energy of the system decreases over time because as the sand falls into the cart, the kinetic energy of the system is converted into other forms of energy, leading to a loss in mechanical energy.

  • What is the concept of underdamping in the context of this video?

    -Underdamping refers to the process where the amplitude of the oscillation decreases over time until the motion eventually stops due to the energy being absorbed into the drag of the fluid or damping medium.

  • How does the addition of sand to the system affect the simple harmonic motion?

    -The addition of sand to the system introduces damping, causing the amplitude of the simple harmonic motion to decrease over time due to the energy being absorbed by the sand.

  • What is the significance of the energy loss in the system?

    -The energy loss in the system signifies a transition from a simple harmonic motion to a damped oscillation, which is a more realistic representation of physical systems where energy is not conserved in the form of mechanical energy alone.

  • How does the graph of the oscillation change with the addition of sand?

    -The graph of the oscillation changes from a simple harmonic motion to a damped oscillation graph, where the amplitude of each cycle becomes smaller until the motion stops.

  • What is the practical application of understanding damped oscillations?

    -Understanding damped oscillations is important in the design of systems like car suspensions and shock absorbers, where the goal is to reduce the amplitude of oscillations to improve stability and performance.

Outlines
00:00
📚 Physics Problem: Mass and Period of Oscillation

The paragraph introduces a physics problem focused on understanding the period of oscillation for a mass-spring system. The scenario involves a cart with a mass of 0.5 kg, with mass being added at a rate of 0.1 kg/s. The challenge is to calculate the time at which the period of oscillation becomes 2T. The speaker explains the process of solving the problem by using the formula for the period of a mass-spring system (T = 2π√(M/K)), and then adjusting the mass to achieve the desired period. The solution involves increasing the mass to 2 kg, which results in the period doubling. The difference in mass and the rate of mass addition are used to calculate the time it takes for the mass to reach the target value, which is found to be 150 seconds.

05:05
📐 Mathematical Solution and Energy Conservation

This paragraph delves into the mathematical aspect of the problem, providing a step-by-step guide on how to set up a proportion to solve for the time it takes to add 1.5 kg to the system. The speaker uses the rate of mass addition and cross-multiplication to find the solution, which is 150 seconds. Additionally, the concept of energy conservation is introduced, explaining that the mechanical energy of the system decreases over time due to the addition of sand. The speaker clarifies that the energy is conserved during an elastic collision but decreases as the sand falls into the cart due to the work done by the system. The paragraph also touches on the non-conservative nature of kinetic energy in this scenario.

10:06
📉 Damping Motion and Energy Loss

The final paragraph discusses the concept of damping motion and its impact on the simple harmonic motion of the mass-spring system. As sand is added to the system, the oscillations begin to dampen over time due to the drag force of the fluid. The speaker explains that the energy gained by the system is absorbed by the drag, leading to a decrease in the amplitude of the oscillations. This process is likened to how car shock absorbers work. The speaker aims to illustrate why the simple harmonic motion loses energy over time as more sand is added, resulting in a smaller amplitude with each cycle. The paragraph concludes with a visual representation of the damping motion, showing how the amplitude decreases with each successive oscillation.

Mindmap
Keywords
💡Simple Harmonic Motion
Simple Harmonic Motion (SHM) is a type of periodic motion where an object oscillates back and forth around an equilibrium position. In the context of the video, SHM is the fundamental behavior of a mass-spring system, where the mass oscillates due to the restoring force of the spring. The video explains how the period of this oscillation can be calculated and how it changes when additional mass is added to the system over time.
💡Mass
In physics, mass is a measure of the amount of matter in an object, and it is a fundamental property that affects the motion of the object when forces are applied. In the video, the mass of the cart is initially 0.5 kg, and it increases over time as more mass is added at a constant rate. This change in mass affects the period of the cart's oscillation in the mass-spring system.
💡Spring Constant
The spring constant, denoted by K, is a measure of the stiffness of a spring. It describes the amount of force required to stretch or compress the spring by a given distance. In the video, the spring constant remains constant while the mass of the cart changes, affecting the period of the oscillation. The spring constant is a key factor in the formula for the period of a mass-spring system's oscillation.
💡Period
The period of an oscillating system is the time it takes for one complete cycle of the motion to occur. In the context of the video, the period is initially determined by the mass and the spring constant of the system. As additional mass is added to the cart over time, the period of the oscillation changes, doubling to 2T as the mass increases.
💡Damping
Damping refers to the reduction of the amplitude of oscillations in a system due to the dissipation of energy. In the video, damping is introduced when sand is added to the cart, which causes the oscillations to lose energy over time. This is a result of the drag or resistance provided by the sand, leading to a decrease in the cart's amplitude of motion.
💡Mechanical Energy
Mechanical energy is the sum of potential and kinetic energy in a mechanical system. It is the energy associated with the motion and position of an object. In the video, the mechanical energy of the system consisting of the spring, cart, and sand is said to decrease over time due to the damping effect introduced by the sand.
💡Conservation of Energy
The principle of conservation of energy states that energy cannot be created or destroyed, only transferred or transformed from one form to another. In the video, it is mentioned that mechanical energy is conserved during an elastic collision, but in the presence of damping (like sand), some of the system's energy is transformed into other forms, leading to a decrease in mechanical energy.
💡Elastic Collision
An elastic collision is a type of collision in which both momentum and kinetic energy are conserved. In the context of the video, the collision between the cart and the sand is considered elastic, but the presence of the sand introduces damping, which leads to a loss of kinetic energy over time.
💡Amplitude
Amplitude in the context of oscillations is the maximum displacement of the oscillating object from its equilibrium position. In the video, the amplitude of the cart's oscillation decreases over time due to the damping effect caused by the addition of sand.
💡Underdamping
Underdamping is a term used in the context of oscillatory systems to describe a situation where the amplitude of the oscillation decreases over time but does not reach zero within a single period. In the video, the addition of sand to the cart creates an underdamped system, where the oscillations gradually decrease in amplitude but continue to oscillate.
💡Work
In physics, work is done when a force causes an object to move in the direction of the force. It is a measure of energy transfer. In the video, work is mentioned in the context of adding energy to the system through the process of damping, where the mechanical energy of the system is transformed into other forms of energy, such as heat.
Highlights

The mass of the cart is given as M equals 0.5 kilograms.

The cart is entering the mass at a rate of 0.1 kilograms per second.

The period of oscillation is required to be 2T, and the initial period is T.

The equation for the period of a mass-spring system is T = 2π√(mass/spring constant).

To achieve a period of 2T, the mass must be adjusted according to the equation.

The final mass is determined to be 2 kilograms by squaring the mass and equating it to 4 times the initial mass.

The difference in mass is calculated as final mass minus initial mass, which is 2 - 0.5 = 1.5 kilograms.

The rate of mass increase is 0.1 kilograms per second, and the total mass to be added is 1.5 kilograms.

It takes 150 seconds to add the required 1.5 kilograms of mass, calculated by dividing the mass difference by the rate of increase.

The mechanical energy of the system, consisting of the spring, cart, and sand, decreases over time.

The system's energy loss is due to the sand falling into the cart, leading to damping motion.

Damping motion is characterized by a decrease in the amplitude of vibration over time.

The concept of damping is applied in car suspensions and shock absorbers to reduce the amplitude of oscillations.

Simple harmonic motion is expected to behave periodically, but the introduction of sand causes the motion to dampen.

The graph of the system's motion should initially resemble simple harmonic motion but will gradually decrease in amplitude due to damping.

The energy loss in the system is attributed to the kinetic energy being absorbed by the sand.

The motion of the system will eventually come to a stop due to the continuous loss of energy.

Transcripts

Browse More Related Video

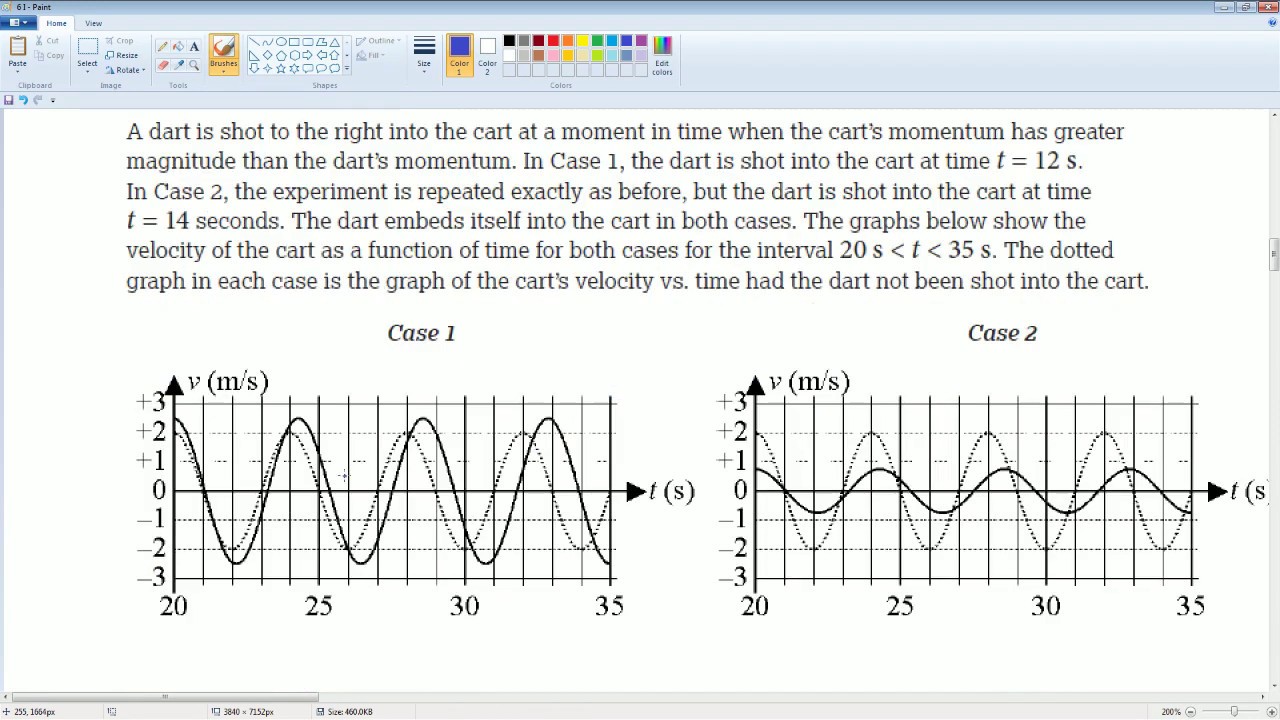
AP Physics Workbook 6.I Changing Mass and Period of a Mass Spring SYstem

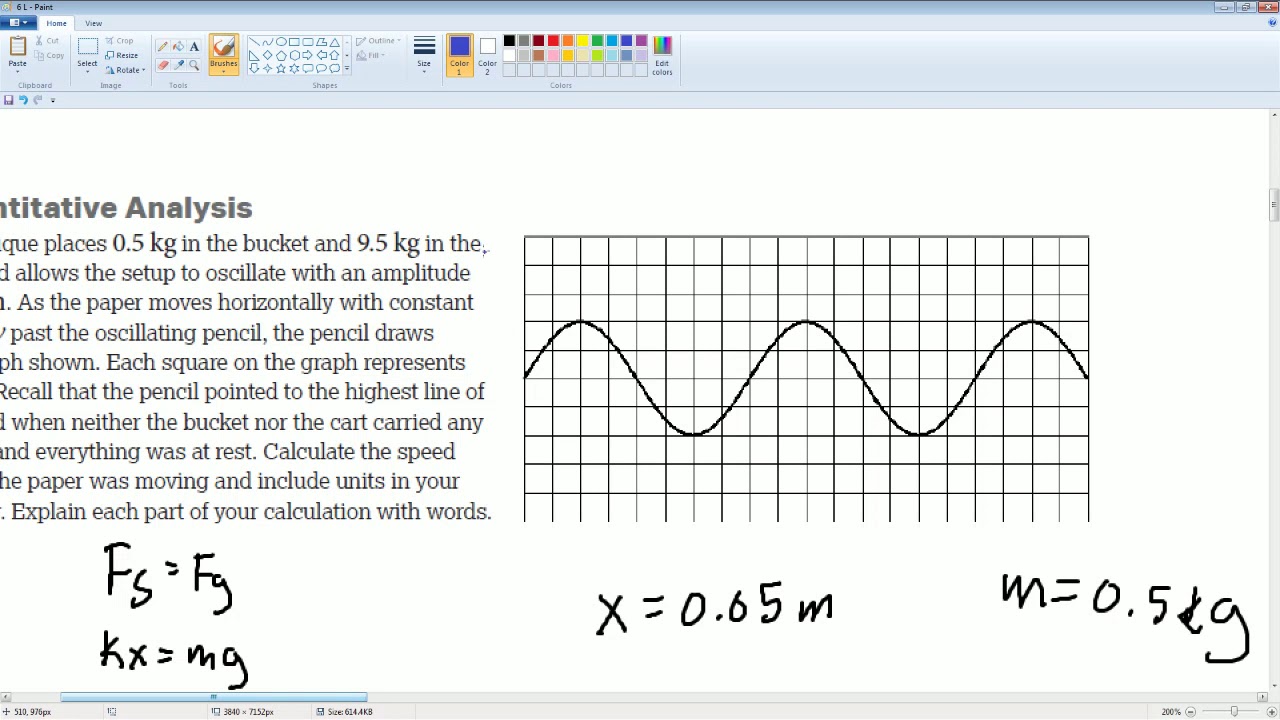
AP Physics Workbook 6.L Sine function of SHM

AP Physics 1: Simple Harmonic Motion Review

AP Physics 1 Simple Harmonic Motion, Mechanical Waves, and Sound Review

Simple Harmonic Motion - Complete Review of the Mass-Spring System

Open & Closed Systems in Energy - IB Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsEducationSimpleHarmonicMotionMassSpringSystemOscillationPeriodMechanicalEnergyDampingEffectElasticCollisionWorkAndEnergyFluidDragCarSuspension