Physics - What Is a Centripetal Force?

The Organic Chemistry Tutor
21 Sept 201810:37
EducationalLearning
32 Likes 10 Comments

TLDRThe video delves into the concept of centripetal force, explaining its role in keeping an object moving in a circular path. It clarifies that centripetal force is not an independent force but results from other forces like tension and static friction. The video uses examples such as a ball on a string and a car turning on a road to illustrate how these forces provide the necessary centripetal force. It also discusses how the gravitational force keeps the Earth in orbit around the Sun. The formula for centripetal force, mv^2/r, is introduced, and the impact of changes in mass, velocity, and radius on the force is explored. The video concludes with a problem-solving approach to understand the effects of these variables on centripetal force.

Takeaways
  • πŸŒ€ Centripetal force is the force that keeps an object moving in a circular path.
  • πŸ”„ When the force and velocity vectors are in the same direction, the object's speed increases.
  • πŸ”„ If the force vector is opposite to the velocity vector, the object slows down.
  • πŸ”„ Centripetal force is always directed towards the center of the circle, causing the object to turn.
  • 🌐 Centripetal force itself is not a force but is caused by other forces like tension or static friction.
  • 🎾 In the example of a ball on a rope, tension force provides the necessary centripetal force for circular motion.
  • πŸš— Static friction provides the centripetal force when a car turns on a road, with the formula being ΞΌs * N ≀ mvΒ²/r.
  • 🌍 Gravitational force is the centripetal force that keeps the Earth in orbit around the Sun.
  • πŸ“ˆ An increase in the mass of an object results in an increase in the required centripetal force.
  • πŸš€ Increasing the speed of an object also increases the centripetal force needed to maintain circular motion.
  • πŸ” If the radius of the circular path is increased, the centripetal force required decreases, as it is inversely proportional to the radius.
Q & A

  • What is the definition of centripetal force?

    -Centripetal force is the force that keeps an object moving in a circular path. It is always directed towards the center of the circle and is caused by other forces, not a force by itself.

  • How does the direction of the force vector relative to the velocity vector affect an object's motion?

    -If the force vector is in the same direction as the velocity vector, the object's speed will increase. If the force vector is in the opposite direction, the object will slow down. If the force vector is perpendicular to the velocity vector, the object will turn without speeding up or slowing down.

  • What provides the centripetal force when a person swings a ball attached to a rope in a circle?

    -The tension force in the rope provides the centripetal force that keeps the ball moving in a circular path.

  • What force provides the centripetal force for a car turning on a road?

    -Static friction provides the centripetal force that allows a car to turn and follow the curvature of the road while moving at a constant speed.

  • What force keeps the Earth in orbit around the Sun?

    -The gravitational force between the Earth and the Sun provides the necessary centripetal force to keep the Earth moving in a nearly circular orbit around the Sun.

  • How does the centripetal force formula mv^2/r relate to the physical quantities involved?

    -The centripetal force formula (mv^2/r) shows that the force required to keep an object moving in a circle is directly proportional to the mass of the object (m), the square of its velocity (v^2), and inversely proportional to the radius of the circular path (r).

  • What happens to the centripetal force if the mass of the object is doubled?

    -If the mass of the object is doubled, the centripetal force will also double, because the mass is in the numerator of the centripetal force formula.

  • How does increasing the velocity of the object affect the required centripetal force?

    -If the velocity of the object is doubled, the required centripetal force will increase by a factor of 4, because the velocity is squared in the centripetal force formula.

  • What is the effect of increasing the radius of the circular path on the centripetal force?

    -If the radius of the circular path is increased, the required centripetal force will decrease, as the radius is in the denominator of the centripetal force formula.

  • If the mass is tripled, the speed is quadrupled, and the radius is halved, what is the overall effect on the centripetal force?

    -The centripetal force will increase by a factor of 96. This is calculated by multiplying the individual effects: (3 for mass) * (4 for speed squared) / (2 for radius) = 96.

  • What should one do to further understand and practice problems related to centripetal force?

    -To further understand and practice centripetal force problems, one can check out the links in the description section of the video, which will provide additional resources and practice problems, as well as exploring the physics video playlist for more structured learning.

Outlines
00:00
πŸŒ€ Introduction to Centripetal Force and its Effects

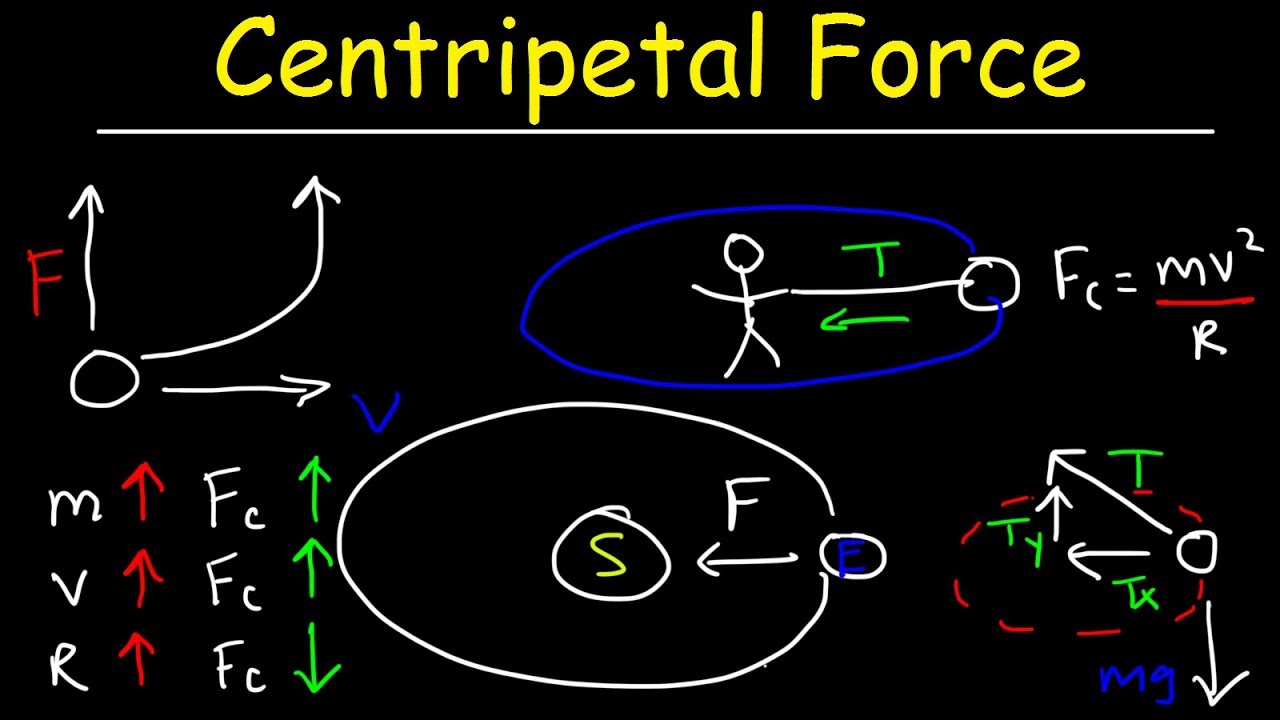
This paragraph introduces the concept of centripetal force, explaining its role in circular motion. It begins by discussing how forces affect an object's velocity when they are in the same or opposite direction. The paragraph then describes centripetal force as a force that acts perpendicular to the velocity vector, causing an object to turn in a circle. It clarifies that centripetal force is not a unique force but is provided by other forces such as tension or static friction. The paragraph provides examples, such as a ball on a string and a car turning on a road, to illustrate how different forces can act as centripetal forces. It concludes with a discussion of gravitational force keeping the Earth in orbit around the Sun, emphasizing the importance of centripetal force in physics.

05:01
πŸ“š Mathematical Relationship and Factors Affecting Centripetal Force

This section delves into the mathematical aspect of centripetal force, using the formula mv^2/r to explain how mass, velocity, and radius influence the force required to maintain circular motion. It discusses the direct relationship between centripetal force and mass and velocity, and the inverse relationship with the radius. The paragraph also explores the effects of doubling the mass, increasing the speed by a factor of two, decreasing the radius by a factor of four, and a combination of tripling the mass, quadrupling the speed, and halving the radius. The explanation is enriched with examples and a method for determining the changes in centripetal force due to variations in these parameters.

10:02
πŸš€ Conclusion and Additional Resources on Centripetal Force

In the concluding paragraph, the video creator summarizes the key points discussed about centripetal force and encourages viewers to explore further through additional resources. The creator provides a link to a playlist of physics videos for a more in-depth understanding and offers help with other challenging subjects like calculus, algebra, and chemistry. The paragraph ends with a call to action for viewers to subscribe to the channel for more educational content, highlighting the availability of resources for a range of topics that can assist in learning and understanding complex subjects.

Mindmap
Keywords
πŸ’‘Centripetal Force
Centripetal force is the key concept discussed in the video. It refers to the force that keeps an object moving in a circular path, directed towards the center of the circle. This force is not a unique force by itself but is caused by other forces such as tension or friction. In the context of the video, examples include the tension in a rope swinging a ball and the static friction that allows a car to turn on a road. The formula for centripetal force is given by mv^2/r, where m is the mass of the object, v is its velocity, and r is the radius of the circular path.
πŸ’‘Velocity Vector
A velocity vector is a vector quantity that describes both the speed and direction of an object's motion. In the video, it is used to explain how forces acting in different directions relative to the velocity vector can affect an object's motion. If a force is in the same direction as the velocity, it will increase the object's speed; if it is opposite, it will decrease the speed; and if it is perpendicular, it will change the direction of the motion without affecting the speed.
πŸ’‘Tension Force
Tension force is the force transmitted through a string, rope, cable, or other similar line when it is pulled tight by forces acting from opposite ends. In the video, tension force is identified as the force that provides the centripetal force necessary to keep a ball moving in a circular path when it is swung around by a person. This force is crucial for maintaining the circular motion.
πŸ’‘Static Friction
Static friction is the frictional force that acts on a stationary object to prevent it from moving. It is the force that keeps an object at rest and can also act as a centripetal force when an object is turning. In the video, static friction is described as the force that allows a car to turn on a road, providing the necessary centripetal force for circular motion.
πŸ’‘Gravitational Force
Gravitational force is the attractive force that exists between any two masses. It is the force that keeps celestial bodies, like the Earth and the Sun, in their orbits. In the video, gravitational force is the centripetal force that keeps the Earth moving in a nearly circular orbit around the Sun. Without this force, the Earth would not follow its orbital path and would instead fly off into space.
πŸ’‘Circular Motion
Circular motion is the movement of an object along a circular path. It is a type of motion where the direction of the velocity is constantly changing, even if the speed remains constant. In the video, circular motion is the focus of the discussion, particularly how centripetal force is necessary for maintaining this type of motion. The video explains that an object in circular motion requires a centripetal force to keep it moving along the circular path.
πŸ’‘Mass
Mass is a measure of the amount of matter in an object, and it is a fundamental property that affects the motion of the object. In the context of centripetal force, mass is a factor that influences the magnitude of the force required to maintain circular motion. The greater the mass, the greater the centripetal force needed to keep an object moving in a circle.
πŸ’‘Radius
The radius is the distance from the center of a circle to any point on its circumference. In the context of circular motion, the radius determines the size of the circle and thus affects the centripetal force required. The radius is an inverse factor in the centripetal force equation (mv^2/r), meaning that a larger radius results in a smaller required centripetal force for an object to maintain its circular motion.
πŸ’‘Speed
Speed is the rate at which an object covers distance, and in the context of circular motion, it refers to how fast an object is moving along the circular path. The speed of an object in a circular motion directly affects the magnitude of the centripetal force needed to maintain that motion. As the speed increases, the centripetal force required also increases, because the object has a greater tendency to move in a straight line (tangentially) rather than follow the circular path.
πŸ’‘Newton's Laws of Motion
While not explicitly mentioned in the video, Newton's Laws of Motion provide the foundational understanding of the forces and motions discussed. The first law, the law of inertia, states that an object will remain at rest or in uniform motion unless acted upon by an external force. Centripetal force is an example of such an external force that acts on an object in circular motion to maintain its state of motion.
πŸ’‘Circular Path
A circular path is a curved trajectory along which an object moves in a constant direction, maintaining a fixed distance from a central point. In the video, the concept of a circular path is central to understanding centripetal force, as it is the path that the force acts to maintain. The circular path is characterized by its radius and the speed at which an object moves along it.
Highlights

Centripetal force is the force that keeps an object moving in a circular path.

When the force and velocity vectors are in the same direction, the object's speed increases.

If the force vector is in the opposite direction to the velocity vector, the object slows down.

A force acting perpendicular to the velocity vector changes the direction of the object without affecting its speed.

Centripetal force always acts towards the center of the circle, hence the name 'center secant force'.

Centripetal force is not a force by itself but is caused by other forces such as tension or static friction.

In the example of a ball on a rope, tension in the rope provides the centripetal force.

For a car turning on a road, static friction provides the centripetal force.

The formula for static friction is mu_s times the normal force, which equals the centripetal force.

In the context of the Earth orbiting the Sun, gravitational force provides the necessary centripetal force.

Without gravity, the Earth would fly off in a tangent away from the Sun.

The centripetal force equation is given by mv^2/r, where m is the mass, v is the velocity, and r is the radius of the circular path.

Increasing the mass of an object increases the centripetal force since mass is in the numerator of the fraction.

If the velocity of the object is increased, the required centripetal force also increases to maintain circular motion.

Doubling the mass of an object doubles the centripetal force, as shown by replacing m with 2 in the equation.

Increasing the speed by a factor of two increases the centripetal force by a factor of 4, as 2 squared equals 4.

Decreasing the radius of the circular path by a factor of 4 increases the centripetal force by a factor of 4, as shown by the calculation 1/(1/4) equals 4.

Tripling the mass, quadrupling the speed, and cutting the radius in half increases the centripetal force by a factor of 96.

The video provides an introduction to centripetal force and its applications in various physical scenarios.

Transcripts

Browse More Related Video

Centripetal Force Physics Problems - Calculate Tension & Maximum Speed - Uniform Circular Motion

Centripetal force and acceleration intuition | Physics | Khan Academy

What is Centripetal force?

Uniform Circular Motion Free Body Diagrams

Centripetal Acceleration & Force - Circular Motion, Banked Curves, Static Friction, Physics Problems

How Many Different Types of Forces Are There In Physics?

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsConceptsCircularMotionCentripetalForceTensionForceStaticFrictionGravitationalForceMathematicalAnalysisEducationalContentHighSchoolPhysicsPhysicsProblems