AP Physics 1 Workbook 1.M Projectile Motion
TLDRThe video script discusses the physics of projectile motion, focusing on a rock thrown horizontally from a cliff. It explains the equations for calculating the time it takes for the rock to hit the ground and the horizontal distance it travels. The script also addresses what changes would occur if the projectile were thrown at an angle, leading to a quadratic equation with different factors. The explanation is technical, aiming to deepen the viewer's understanding of the principles behind projectile motion.
Takeaways
- 📚 The transcript discusses the physics of projectile motion, specifically focusing on a rock thrown horizontally from a cliff.
- 🌐 The scenario involves choosing a coordinate system with the origin at the base of the cliff and positive directions defined as up and to the right.
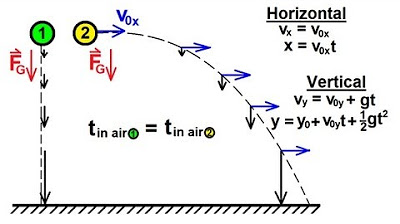
- 📈 The vertical motion of the projectile is described by a parabolic trajectory, while the horizontal motion is linear.
- 🔢 The time it takes for the rock to hit the ground is determined by the vertical height (H) and the acceleration due to gravity (g), using the equation T = √(2H/g).
- 🎯 The horizontal distance (D) the rock travels is calculated using the initial horizontal velocity (Vx0) and the time of flight (T), with the formula D = Vx0 * T.
- 🔄 If the rock is thrown at an angle above the horizontal, the motion becomes more complex, involving both horizontal and vertical components of velocity.
- 📌 The equations for projectile motion must be adjusted to account for the angle of projection, leading to a quadratic equation in terms of time.
- 🚀 The initial velocity components (Vx0 and Vy0) are key in determining the trajectory and the time of flight for angled projectile motion.
- 🧮 The transcript emphasizes the importance of understanding the underlying physics principles and how they translate into mathematical equations.
- 🛠️ The process of solving these problems involves algebraic manipulation and substitution of known values to find the desired quantities.
- 📝 The script serves as a guide for solving problems related to projectile motion, highlighting the steps and considerations needed to arrive at the correct solutions.
Q & A
What type of motion is being discussed in the video?
-Projectile motion is being discussed, specifically focusing on horizontal projectile motion.
What is the scenario described in the video?
-The scenario involves a rock being thrown horizontally from the top of a cliff with a given height (H) and initial velocity (V).
How is the coordinate system set up in the problem?
-The coordinate system is traditionally set up with the positive x-direction going to the right and the positive y-direction going upwards.
What is the key equation used to solve for the time it takes for the rock to hit the ground?
-The key equation used is Y = Y_not + vy_not*t + (1/2)g*t^2, which is rearranged to solve for time (t) as t = sqrt(2*H/g).
How is the horizontal distance traveled by the projectile calculated?
-The horizontal distance (D) is calculated using the equation D = v_not_x*t, where v_not_x is the horizontal component of the initial velocity and t is the time of flight.
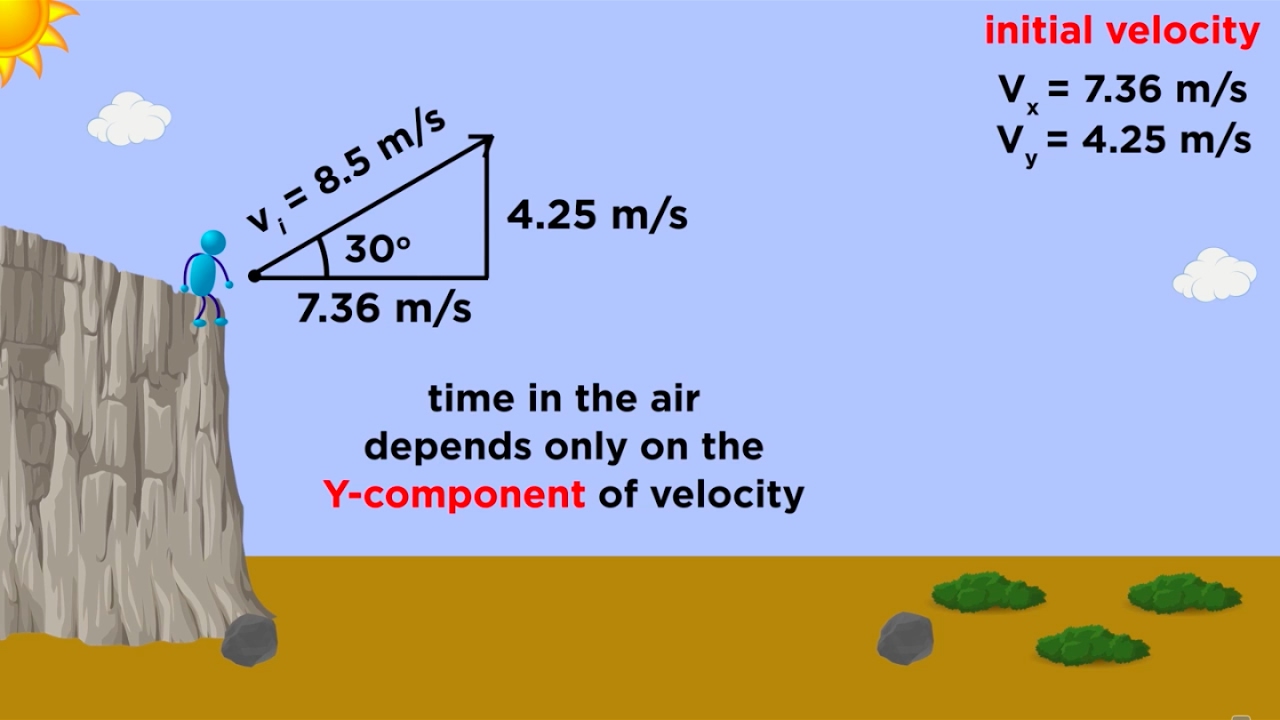
What changes would occur if the projectile was thrown at an angle above the horizontal?
-If thrown at an angle, there would be a vertical component of the initial velocity (v_not_y), leading to a quadratic equation in terms of time (t) and requiring a different approach to solve for the time of flight.
Why does the vertical velocity component (vy_not) equal zero in the horizontal projectile motion scenario?
-The vertical velocity component (vy_not) equals zero because the rock is thrown horizontally, meaning there is no initial upward or downward motion.
What is the significance of the acceleration due to gravity (g) in the projectile motion equations?
-The acceleration due to gravity (g) is significant as it affects the vertical motion of the projectile, causing the object to accelerate downwards and determining the time it takes to hit the ground.
How does the horizontal acceleration (ax) affect the projectile's motion?
-In the case of horizontal projectile motion, the horizontal acceleration (ax) is zero because there is no horizontal force acting on the projectile once it is in the air.
What is the relationship between the initial velocity (V), the height (H), and the time (t) it takes for the projectile to hit the ground?
-The relationship is given by the equation for the vertical motion (Y component), where Y = v_not_y*t + (1/2)g*t^2. Since v_not_y is zero for horizontal motion, it simplifies to Y = (1/2)g*t^2, and solving for t yields t = sqrt(2*H/g).
What is the significance of the quadratic equation in the context of the projectile motion when thrown at an angle?
-The quadratic equation represents the combined motion of the projectile in both the x and y directions when thrown at an angle. It shows that the time of flight (t) is a function of both the horizontal and vertical components of the initial velocity, leading to a more complex solution.
Outlines
📚 Introduction to Projectile Motion
The paragraph introduces the topic of projectile motion within the context of AP Physics. It sets the scenario of a rock being thrown horizontally from the top of a cliff with an initial velocity (V) and height (H). The speaker explains the need to label the origin (zero-zero) and choose positive directions for both horizontal and vertical axes on the diagram. The focus is on identifying the correct equation to solve for the time it takes for the rock to hit the ground. The speaker emphasizes understanding the nature of motion, distinguishing between linear and parabolic trajectories, and selecting the appropriate formula from the formula sheet to solve the problem.
🧮 Solving for Time and Horizontal Distance
This paragraph delves into the process of solving for the time (T) it takes for the rock to hit the ground and the horizontal distance (D) it travels. The speaker clarifies that the initial vertical velocity is zero since the rock is thrown horizontally. The equation for height (Y) is rearranged to solve for time, resulting in the formula T = √(2H/G). The speaker then explains how to find the horizontal distance using the time derived from the previous calculation, leading to the equation D = Vx0 * T. The paragraph emphasizes the importance of understanding the separate components of motion and how they contribute to the overall problem-solving process.
🔄 Changes in Equations for Angled Projectiles
The speaker discusses how the equations from the previous paragraphs would change if the projectile were thrown at an angle above the horizontal. The introduction of a horizontal velocity component (Vx) and vertical velocity component (Vy) due to the angle of projection is explained. The speaker points out that certain terms in the equations do not cancel out as they would in the case of horizontal projection, leading to a more complex quadratic equation in terms of time (T). The paragraph emphasizes the need to understand how the components of velocity and the angle of projection affect the overall motion of the projectile.
🎥 Summary of Projectile Motion Concepts
In the final paragraph, the speaker wraps up the discussion on projectile motion by summarizing the key points covered in the previous sections. The speaker reiterates that the velocity of projection affects both the distance and speed at which the object is thrown. The paragraph serves as a recap, reinforcing the concepts of projectile motion, the importance of understanding the separate horizontal and vertical components of motion, and the mathematical approach to solving such problems.
Mindmap
Keywords
💡Projectile Motion
💡Horizontally Thrown
💡Cliff Height (H)
💡Velocity (V)
💡Time (T)
💡Horizontal Distance (D)
💡Acceleration (a)
💡Gravity (G)
💡Equations of Motion
💡Angle of Projection
Highlights
The scenario involves a rock thrown horizontally from a cliff, which is a classic example of projectile motion. (Start time: 0s)
The choice of origin and positive direction is important for problem-solving, with the convention being right and up as positive. (Start time: 8s)
The equation for time of flight in projectile motion is derived from the vertical motion component. (Start time: 33s)
The key equation for time (t) is t = √(2H/G), where H is the height and G is the acceleration due to gravity. (Start time: 1m 47s)
Horizontal distance (D) is determined by the initial horizontal velocity (Vx0) and time (t), with the equation D = Vx0 * t. (Start time: 2m 26s)
When the projectile is thrown at an angle, the vertical component of velocity (Vy0) becomes non-zero, altering the equations. (Start time: 3m 40s)
The quadratic nature of the projectile motion equations is emphasized, particularly when the angle of projection is not horizontal. (Start time: 4m 10s)
The impact of the angle of projection on the trajectory and the resulting change in the equations is discussed. (Start time: 4m 30s)
The video provides a step-by-step approach to solving projectile motion problems, emphasizing the importance of understanding the underlying physics. (Start time: throughout)
The use of diagrams and visual aids, such as Paint, is recommended for better understanding and problem-solving. (Start time: 1m 50s)
The transcript highlights the importance of distinguishing between horizontal and vertical components of motion and how they affect the overall motion. (Start time: throughout)
The video demonstrates the application of basic principles of physics, such as Newton's laws of motion, to real-world scenarios. (Start time: throughout)
The process of simplifying and solving equations is shown, with an emphasis on correctly identifying and applying the relevant physical constants and variables. (Start time: 2m 40s)
The transcript serves as a comprehensive guide for students learning to tackle projectile motion problems, providing both theoretical insights and practical problem-solving strategies. (Start time: throughout)
Transcripts
Browse More Related Video

Physics 3.5.4a - Projectile Practice Problem 1

AP Physics B Kinematics Presentation General Problems #10

AP Physics 1 Workbook 1.N Projectile Motion Part 2 Solution
Kinematics Part 3: Projectile Motion

Projectile Launched of a Cliff
Physics 3: Motion in 2-D Projectile Motion (1 of 21) Independent Motion in x and y
5.0 / 5 (0 votes)
Thanks for rating: