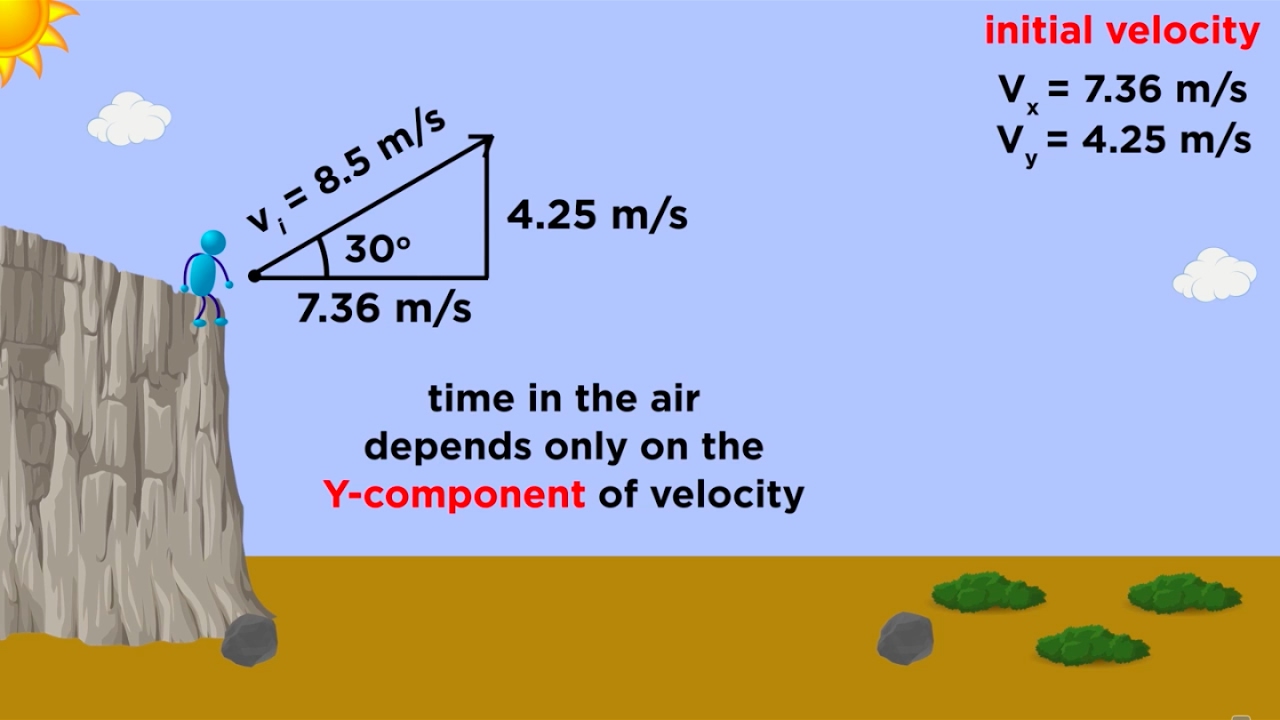
Physics 3.5.4a - Projectile Practice Problem 1
TLDRThe video script presents a detailed walkthrough of solving a projectile motion problem, where a rock is thrown horizontally from a 100-meter cliff and lands 95 meters away. The key concept emphasized is to analyze the horizontal and vertical components of the motion independently. By first solving the vertical motion to find the time it takes for the rock to fall, and then using this time to determine the horizontal velocity, the problem is methodically broken down into manageable steps, ultimately revealing that the rock was thrown at a speed of 21 m/s.
Takeaways
- 🎯 The problem involves a horizontally thrown rock off a 100m cliff landing 95m away.
- 📐 To solve projectile motion problems, separate horizontal and vertical motions as they are independent of each other.
- 🌐 The vertical motion is analyzed first to find the time it takes for the rock to fall from the cliff to the ground.
- 🚀 The initial velocity for vertical motion is considered zero since the rock is thrown horizontally.
- 📉 The equation for vertical motion is Y = 0 + 0 + (1/2)gt^2, where 'g' is the acceleration due to gravity (9.8 m/s^2).
- 🕒 Time is calculated using the rearranged equation t = √(2Y/a), which yields 4.52 seconds for the rock to fall.
- 🏃 For horizontal motion, the equation is simplified to x = v0t, as there is no acceleration in the horizontal direction.
- 🏞️ The horizontal distance (95m) and the time (4.52s) are used to find the initial horizontal velocity (v0), which is 21 m/s.
- 🤔 The approach of trying the horizontal motion first would indicate that more information is needed, hinting to solve the vertical motion first.
- 🧠 Understanding the concepts and calculations involved in projectile motion problems is essential for accurate problem-solving.
Q & A
What is the main concept discussed in the transcript?
-The main concept discussed in the transcript is projectile motion, specifically focusing on how to solve problems involving horizontal and vertical motion components separately.
Why is it important to solve horizontal and vertical motions independently in projectile problems?
-It is important because the horizontal and vertical motions do not affect each other. This approach allows for simpler and more manageable calculations, making it easier to understand and solve the problem.
What is the initial velocity of the rock thrown horizontally in the example provided?
-The initial velocity of the rock thrown horizontally is not given directly, but it can be determined using the information about the horizontal distance and the time of flight calculated from the vertical motion.
How is the acceleration due to gravity treated in the vertical motion equation?
-In the vertical motion equation, the acceleration due to gravity is treated as a constant value of 9.8 m/s^2, directed downwards. In this problem, 'down' is considered the positive direction, so the acceleration is positive.
What is the formula used to calculate the time of flight in the vertical motion?
-The formula used to calculate the time of flight in the vertical motion is derived from the equation y = y0 + v0*t + 0.5*a*t^2, which simplifies to t = sqrt(2*y/a) since the initial velocity (v0) is zero and the initial height (y0) is also zero.
How is the horizontal distance of 95 meters related to the time of flight calculated from the vertical motion?
-The horizontal distance of 95 meters is used in conjunction with the time of flight calculated from the vertical motion to determine the initial horizontal velocity of the rock. This is done using the formula x = v0*t, where x is the horizontal distance, and t is the time of flight.
What is the final calculated initial horizontal velocity of the rock?
-The final calculated initial horizontal velocity of the rock is 21 m/s.
Why was the vertical motion calculated before the horizontal motion in the example?
-The vertical motion was calculated first because it provided the necessary time of flight, which is required to solve for the horizontal velocity in the horizontal motion equation.
What would be the first clue to know that you need to switch to solving the vertical motion first?
-The first clue is when you realize that you don't have enough information to solve for the initial horizontal velocity (v0) in the horizontal motion equation, indicating that you need to find the time of flight from the vertical motion first.
How does the concept of projectile motion apply to real-world scenarios?
-Projectile motion is a fundamental concept in physics that can be applied to various real-world scenarios such as sports (e.g., throwing a ball), engineering (e.g., designing trajectories for rockets or projectiles), and understanding the motion of objects under the influence of gravity and air resistance.
What is the significance of understanding the separate horizontal and vertical components of motion?
-Understanding the separate components of motion is significant because it allows for a more detailed analysis of an object's trajectory, which can be crucial in various applications, from predicting the behavior of projectiles to calculating the effects of external forces on an object's path.
Outlines
🚀 Understanding Projectile Motion - The Vertical Aspect
This paragraph delves into the concept of projectile motion, specifically focusing on the vertical component. It emphasizes the importance of attempting to solve problems independently to reinforce understanding. The example given involves a rock thrown horizontally off a 100m cliff, landing 95m away. The key takeaway is the method of solving the problem by separating the horizontal and vertical aspects, treating them as two distinct issues. The vertical motion is calculated first to determine the time it takes for the rock to fall, using the equation Y = 1/2 * a * t^2, where 'a' is the acceleration due to gravity (9.8 m/s^2) and 't' is the time in seconds. By setting the initial position as zero and the final position as 100m, the equation is simplified, and solving for 't' yields a time of 4.52 seconds. This approach highlights the significance of understanding the independent nature of horizontal and vertical motion in projectile problems.
🌟 Solving for Horizontal Velocity - The Final Step
The second paragraph continues the projectile motion analysis by focusing on the horizontal aspect. After calculating the time of fall from the vertical motion (4.52 seconds), this information is used to determine the horizontal velocity. The explanation clarifies that since there is no horizontal acceleration (the rock is thrown horizontally), the equation simplifies to x = v0 * t, where 'x' is the horizontal distance (95m) and 'v0' is the initial horizontal velocity. By rearranging the equation to solve for 'v0', the initial velocity is found to be 21 m/s. The paragraph concludes by advising that if one were to attempt the horizontal motion first without knowing the time of flight, it would be impossible to solve the problem, indicating the necessity of addressing the vertical motion before the horizontal in projectile problems. The summary underscores the importance of grasping the fundamental concepts and calculations involved in projectile motion analysis.
Mindmap
Keywords
💡Projectile Motion
💡Horizontally
💡Initial Velocity
💡Acceleration
💡Parabolic Trajectory
💡Cliff
💡Time
💡Horizontal Distance
💡Free Fall
💡Equations of Motion
Highlights
The problem involves a rock thrown horizontally off a 100m cliff.
The rock lands 95 meters away from the base of the cliff.
The motion of the rock follows a parabolic path.
The key to solving projectile problems is to analyze horizontal and vertical motions independently.
The vertical motion is considered first to find the time it takes for the rock to fall.
The acceleration due to gravity is 9.8 m/s^2 and is considered positive in the downward direction for this problem.
The initial velocity for the vertical motion is zero since the rock is thrown horizontally.
The equation for vertical motion is y = (1/2)gt^2, where g is the acceleration due to gravity and t is time.
Solving for time (t) gives us t = √((2y)/g), which is 4.52 seconds for this problem.
The horizontal motion is then analyzed using the time found from the vertical motion.
The equation for horizontal motion is x = v0t, where x is the horizontal distance, v0 is the initial horizontal velocity, and t is time.
The initial horizontal velocity (v0) is calculated to be 21 m/s using the horizontal distance and time.
The problem-solving approach emphasizes the importance of understanding the concepts and calculations involved in projectile motion.
The method demonstrates the practical application of physics principles in analyzing real-world scenarios.
The transcript serves as a guide for learners to practice and enhance their problem-solving skills in projectile motion.
The problem-solving process is structured in a step-by-step manner, making it easier for learners to follow and understand.
The use of algebraic manipulation is highlighted in solving for the unknown variables in projectile motion equations.
The transcript emphasizes the value of attempting problems independently to reinforce learning and retention of concepts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: