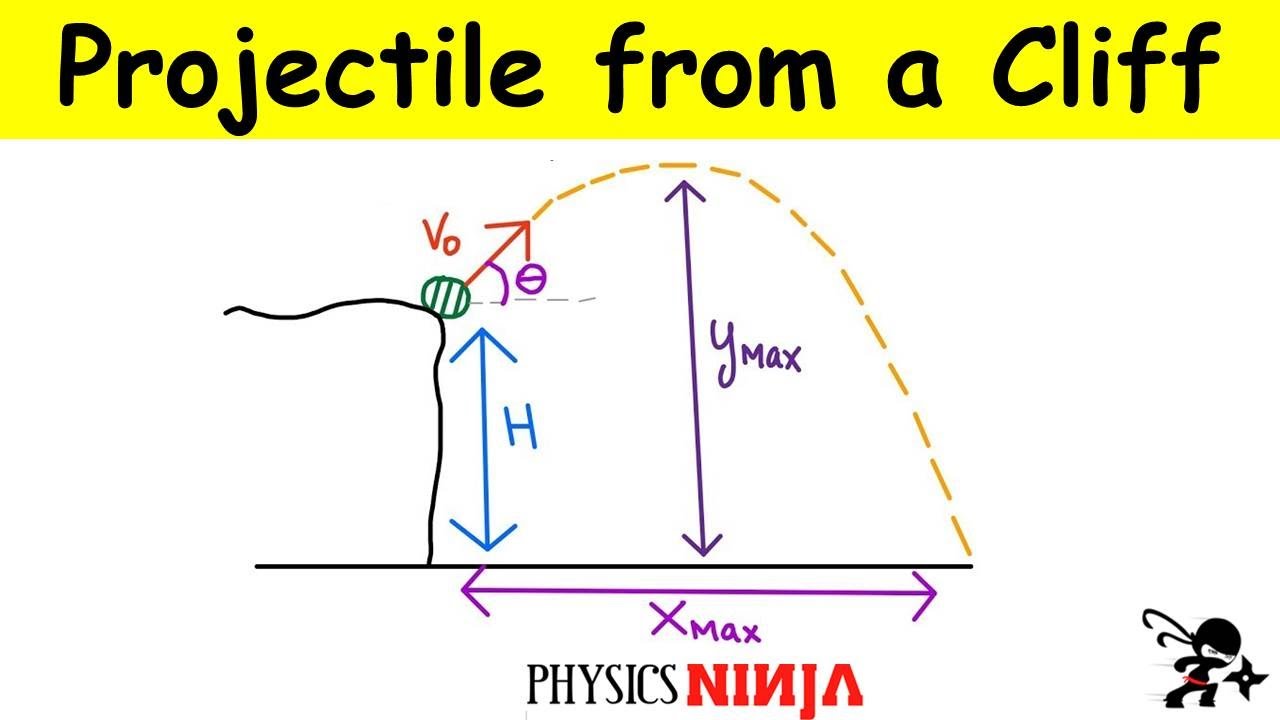
Projectile Launched of a Cliff
TLDRThe video script discusses the physics of a projectile motion, specifically an object launched horizontally from a cliff with an initial velocity of 20 m/s and a height of 15 m. It explains how to calculate the time the object is in the air, the distance it travels, and its final velocity using the equations of motion. The analysis involves breaking down the motion into horizontal and vertical components, and solving for variables such as time of flight, horizontal distance, and final velocity. The final results indicate the object takes approximately 1.75 seconds to fall, travels 35 meters horizontally, and has a final velocity of 26.3 m/s at an angle of 40.7 degrees to the horizontal.
Takeaways
- 🚀 The problem involves calculating the time, distance, and final velocity of a projectile launched horizontally from a cliff with an initial velocity of 20 m/s and a height of 15 m.
- ⏳ Time in the air (T) is calculated by the formula T = √(2H/g), where H is the height and g is the acceleration due to gravity (9.8 m/s²). For this scenario, T is approximately 1.75 seconds.
- 📏 The horizontal distance (X) traveled by the projectile is determined by multiplying the initial horizontal velocity (V₀) by the time in the air (T), resulting in approximately 35 meters.
- 📉 The vertical component of the velocity (Vy) at the bottom is calculated by the formula Vy = -gT, which gives a value of -17.2 m/s (negative because it's directed downwards).
- 🏹 The final velocity (V) is found using the Pythagorean theorem, combining the horizontal (Vx) and vertical (Vy) components, resulting in a magnitude of approximately 26.3 m/s.
- 📐 The angle (θ) between the final velocity vector and the horizontal is determined by the arctangent of Vy/Vx, which gives an angle of approximately 40.7 degrees.
- 🔄 The projectile motion consists of two components: horizontal motion with constant velocity and vertical motion with acceleration due to gravity.
- 🌐 The horizontal and vertical motions are analyzed separately, with the horizontal motion being unaffected by gravity and the vertical motion being influenced by gravity alone.
- 🔢 The problem-solving process involves setting up equations for each component of motion, solving for the unknowns, and then combining the results to answer the questions.
- 🎯 The key to solving these problems is understanding the kinematic equations and how to apply them to the specific components of motion in projectile scenarios.
- 📚 The script serves as a tutorial for solving projectile motion problems, emphasizing the importance of analyzing the motion in both horizontal and vertical directions and the use of algebra to find the solutions.
Q & A
What is the initial velocity given for the object in the script?
-The initial velocity given for the object in the script is 20 meters per second.
What is the height of the cliff from which the object is launched?
-The height of the cliff from which the object is launched is 15 meters.
What is the term used to describe the time the object is in the air?
-The term used to describe the time the object is in the air is 'time T'.
How is the total time of flight calculated for the projectile?
-The total time of flight for the projectile is calculated using the formula T = √(2H/g), where H is the height, g is the acceleration due to gravity (9.8 m/s²), and T is the time in seconds.
What is the total horizontal distance traveled by the projectile?
-The total horizontal distance traveled by the projectile is calculated by multiplying the initial horizontal velocity (V0) by the time of flight (T). In this case, it is 20 m/s * 1.75 s, which equals approximately 35 meters.
What is the final velocity of the projectile just before it hits the ground?
-The final velocity of the projectile just before it hits the ground is calculated using the Pythagorean theorem with the horizontal (Vx) and vertical (Vy) components of the velocity. The magnitude of the final velocity is approximately 26.3 m/s.
What is the angle of the final velocity vector with respect to the horizontal just before the projectile hits the ground?
-The angle of the final velocity vector with respect to the horizontal just before the projectile hits the ground is found using the arctangent function, tan^(-1)(Vy/Vx). In this case, it is approximately 40.7 degrees.
Why does the acceleration in the X-direction remain zero throughout the projectile's motion?
-The acceleration in the X-direction remains zero throughout the projectile's motion because there are no forces acting in the horizontal direction (assuming no air resistance), and thus the horizontal velocity remains constant.
How does the acceleration due to gravity affect the Y-component of the projectile's velocity?
-The acceleration due to gravity affects the Y-component of the projectile's velocity by causing it to decrease over time as the object falls. This is represented by the equation Vy = -gt, where g is the acceleration due to gravity and t is the time.
What is the significance of the figure shown in the script that compares a projectile launched with a horizontal speed to one dropped vertically?
-The figure highlights that both the horizontally launched projectile and the vertically dropped object take the same amount of time to reach the ground from the same initial position, despite following different trajectories.
What is the role of the XY coordinate system in solving this problem?
-The XY coordinate system is used to separate the motion of the projectile into its horizontal (X) and vertical (Y) components, allowing for easier analysis and calculation of the projectile's position, velocity, and acceleration in each direction.
How does the script demonstrate the use of kinematic equations in solving projectile motion problems?
-The script demonstrates the use of kinematic equations by setting up and solving equations for the projectile's X and Y positions, velocities, and accelerations at various points in its trajectory, ultimately providing the time of flight, horizontal distance traveled, final velocity, and the angle of the final velocity vector.
Outlines
🚀 Initial Conditions and Problem Setup
The paragraph begins by establishing the initial conditions for a projectile motion problem, with an initial velocity of 20 m/s and a height of 15 meters. The main objective is to determine the time (T) the object is in the air, the horizontal distance (X) it travels, and its final velocity (V) just before impact. The discussion introduces the concept of separating the motion into horizontal (X-direction) and vertical (Y-direction) components, and emphasizes that the acceleration due to gravity (g = 9.8 m/s^2) only affects the vertical motion. The paragraph sets up a standard XY coordinate system with the origin at the base of the cliff and explains how to handle the algebraic equations to solve the problem.
🕒 Time of Flight and Horizontal Distance Calculation
This paragraph focuses on calculating the time of flight and the horizontal distance traveled by the projectile. It explains that the time taken for the projectile to fall from its initial position to the ground is the same, regardless of its trajectory. The speaker uses the equations of motion to find the time (T) it takes for the object to reach the ground, which is determined to be 1.75 seconds. The horizontal distance (X) is then calculated using the initial velocity and the time of flight, resulting in a distance of approximately 35 meters.
🏹 Final Velocity and Impact Angle Determination
The final paragraph deals with calculating the final velocity and the angle of impact of the projectile. The speaker first explains how to find the horizontal (Vx) and vertical (Vy) components of the velocity just before impact. The horizontal component remains constant at the initial velocity of 20 m/s, while the vertical component is calculated using the acceleration due to gravity and the time of flight. With both components known, the final velocity is found using the Pythagorean theorem, resulting in a magnitude of 26.3 m/s. The impact angle is then determined using the tangent function and the components of velocity, yielding an angle of 40.7 degrees.
Mindmap
Keywords
💡initial velocity
💡height
💡time in the air
💡displacement
💡final velocity
💡components of velocity
💡acceleration due to gravity
💡trajectory
💡Pythagorean theorem
💡angle of impact
Highlights
Initial velocity given as 20 meters per second.
Height of the projectile's launch is 15 meters.
Time in the air (T) is calculated from the launch point to the ground impact point.
Projectile motion involves both horizontal and vertical components.
The time taken for projectile and freely falling object to reach the ground is the same, regardless of trajectory.
The X coordinate system is defined with the origin at the base of the cliff, with X=0 and Y=0 at the launch position.
In the X direction, the acceleration is zero, and the velocity remains constant.
In the Y direction, the acceleration is -9.8 m/s^2, directed downwards.
The horizontal distance (X) traveled can be calculated using the initial horizontal velocity and time in the air.
The final velocity is determined by both the horizontal and vertical components of velocity.
The angle of the final velocity vector with respect to the horizontal can be found using the components and trigonometric relationships.
The time of flight (T) is approximately 1.75 seconds, calculated using the height and acceleration due to gravity.
The horizontal distance (X) traveled is approximately 35 meters.
The final velocity has a magnitude of approximately 26.3 m/s and makes an angle of 40.7 degrees with the horizontal.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: