Kinematics Part 3: Projectile Motion
TLDRThis video script delves into the concept of projectile motion, explaining how it involves an object moving both horizontally and vertically, and how these motions are independent of each other. It uses the example of a cannonball fired at an angle to illustrate how the path can be represented by a parabola and how the motion can be dissected into x (horizontal) and y (vertical) components using kinematic equations. The script further demonstrates how to calculate the time of flight and the horizontal distance traveled by a rock thrown at a 30-degree angle from a cliff with an initial velocity of 8.5 m/s, emphasizing the application of trigonometry and the constant acceleration due to gravity.
Takeaways
- 📚 Projectile motion involves an object moving in both horizontal and vertical directions, such as a thrown object.
- 🌟 The horizontal and vertical motions of an object in projectile motion are independent of each other, allowing for separate analysis.
- 🔄 The path of projectile motion can be represented by a parabolic curve, similar to the trajectory of a fired cannonball.
- 📐 To analyze projectile motion, one must split the velocity vector into its horizontal (V sub X) and vertical (V sub Y) components using trigonometry.
- 🚀 The initial velocity of an object in projectile motion can be decomposed using the cosine and sine of the launch angle to find the x and y components.
- 🕒 The time an object spends in the air during projectile motion is determined solely by its vertical motion and is independent of its horizontal velocity.
- 🏆 The horizontal distance traveled by an object in projectile motion depends on its horizontal velocity and the time it spends in the air.
- 🔢 To calculate the time of flight and horizontal distance, one can use the kinematic equations, focusing on the relevant components of motion for each.
- 📈 The vertical component of velocity decreases over time due to constant acceleration caused by gravity until it reaches the ground.
- 🎯 Understanding projectile motion is essential for solving real-world problems like calculating the distance and time of a rock thrown off a cliff.
- 💡 Analyzing projectile motion as a combination of one-dimensional motions simplifies the process and allows for accurate predictions of the object's path and landing point.
Q & A
What is projectile motion?
-Projectile motion refers to the movement of an object that is thrown or launched into the air, moving simultaneously in both horizontal and vertical directions, such as a cannonball fired at an angle from the horizontal.
How are the horizontal and vertical motions of a projectile related?
-The horizontal and vertical motions of a projectile are completely independent of each other. This means that one can analyze the motion in each direction separately using different equations, corresponding to the x-coordinates and y-coordinates of the object respectively.
What is the significance of the parabolic path in projectile motion?
-The parabolic path represents the trajectory of a projectile in motion. It is a curve that describes the combined horizontal and vertical movements of the object, illustrating how the object's path is influenced by the initial conditions and gravity.
How can the motion of two marbles, one dropped and one rolled off a surface, demonstrate the independence of horizontal and vertical motions?
-If two marbles are released simultaneously, one from rest and the other with a horizontal velocity, they will hit the ground at the same time because their vertical motion is unaffected by the horizontal motion. This demonstrates that the horizontal and vertical motions are independent and can be analyzed separately.
What are the components of the velocity vector in projectile motion?
-The velocity vector in projectile motion can be split into horizontal (V_sub_X) and vertical (V_sub_Y) components. The horizontal component remains constant throughout the motion, while the vertical component decreases over time due to the acceleration of gravity acting downwards.
How can one calculate the initial velocity components for a projectile thrown at an angle?
-The initial velocity components for a projectile thrown at an angle can be calculated using trigonometry. The horizontal component (V_sub_X) is found by multiplying the initial velocity by the cosine of the angle, and the vertical component (V_sub_Y) is found by multiplying the initial velocity by the sine of the angle.
What is the relationship between the time a projectile spends in the air and its vertical motion?
-The time a projectile spends in the air is determined solely by its vertical motion. Regardless of the horizontal velocity, the projectile will stop being in the air when it hits the ground, so the time in the air is a characteristic of the vertical motion and is independent of horizontal motion.
How can one determine the distance a projectile travels horizontally?
-The horizontal distance a projectile travels can be determined by multiplying the horizontal velocity component by the time the projectile is in the air. This calculation assumes no air resistance and that the projectile moves at a constant horizontal velocity throughout its trajectory.
What is the effect of gravity on the vertical velocity component of a projectile?
-Gravity causes a constant acceleration in the negative (downward) direction, affecting the vertical velocity component of the projectile. This acceleration reduces the vertical velocity to zero at the peak of the trajectory (zenith) and then causes it to become increasingly negative as the projectile descends towards the ground.
What is the process for calculating the time a projectile is in the air?
-To calculate the time a projectile is in the air, one can treat it as a one-dimensional vertical motion problem, focusing on the y-component of the velocity vector. Using the equations of motion with the initial vertical velocity, acceleration due to gravity, and displacement (which is negative for upward motion), one can solve for the time using the quadratic formula.
How can one use the principles of projectile motion to solve real-world problems, such as throwing a rock off a cliff?
-By understanding the independence of horizontal and vertical motions and applying the principles of projectile motion, one can analyze real-world scenarios like throwing a rock off a cliff. By calculating the time the rock is in the air (using vertical motion) and the horizontal distance traveled (using horizontal motion), one can predict where the rock will land.
Outlines
🚀 Understanding Projectile Motion
This paragraph introduces the concept of projectile motion, explaining how it differs from horizontal and vertical motion. It uses the example of a cannonball fired at an angle to illustrate how an object's horizontal and vertical movements are independent of each other. The importance of separating the motion into x (horizontal) and y (vertical) components is emphasized, and the idea that these components can be analyzed using separate equations is introduced. The concept is further clarified with the analogy of two marbles, one dropped and one rolled off a surface at the same height, highlighting that their times to hit the ground are identical despite different horizontal motions.
📐 Calculating Projectile Motion
In this paragraph, the process of calculating the time a projectile spends in the air and the distance it travels is detailed. The example of a rock thrown at a 30-degree angle from the edge of a cliff with an initial velocity of 8.5 m/s is used to demonstrate how to apply the principles of projectile motion. The paragraph explains how to separate the rock's velocity into horizontal (V sub X) and vertical (V sub Y) components using trigonometry, and how these components are used to determine the time of flight and horizontal distance traveled. The calculation shows that the rock will be in the air for 4.97 seconds and will land about 36.6 meters away from the cliff edge, reinforcing the idea that projectile motion can be analyzed as a combination of one-dimensional motions in the x and y directions.
Mindmap
Keywords
💡Projectile Motion
💡Kinematic Equations
💡Horizontal Motion
💡Vertical Motion
💡Independent Motion
💡Velocity Components
💡Zenith
💡Acceleration
💡Trigonometry
💡Parabolic Trajectory
💡Airtime
Highlights
Projectile motion is the movement of an object that is thrown or launched into the air, moving in both horizontal and vertical directions simultaneously.
In projectile motion, the horizontal and vertical motions are completely independent of each other, allowing for separate analysis of each component.
The path of a projectile motion can be represented by a parabolic curve, similar to the trajectory of a cannonball fired at an angle from the horizontal.
Two marbles dropped from the same height with and without horizontal velocity will hit the ground at the same time, demonstrating the independence of vertical and horizontal motions.
The horizontal velocity remains constant throughout the projectile motion, disregarding wind resistance, while the vertical velocity decreases due to gravity.
To analyze projectile motion, the initial velocity vector must be split into horizontal (V sub X) and vertical (V sub Y) components using trigonometry.
The initial velocity in the X direction can be calculated using the cosine of the launch angle, and the initial velocity in the Y direction using the sine of the launch angle.
A rock thrown straight up with the same initial vertical velocity as one thrown at an angle will land at the same time, highlighting the independence of the vertical motion.
The time a projectile spends in the air is determined by its vertical motion, and can be calculated using one-dimensional vertical motion equations.
The horizontal distance traveled by a projectile can be found by multiplying the horizontal velocity by the time the projectile is in the air.
This tutorial provides a comprehensive understanding of projectile motion by breaking down complex concepts into manageable parts and applying them to real-world examples.
The combination of one-dimensional horizontal and vertical motions allows for the analysis of more complex, two-dimensional projectile motion scenarios.
The tutorial uses the example of throwing a rock off a cliff at an upward angle to illustrate how to calculate both the time in the air and the horizontal distance traveled.
By understanding the principles of projectile motion, one can solve a variety of problems involving objects moving in both horizontal and vertical directions.
The use of trigonometry to split the velocity vector into components is a key method in the analysis of projectile motion.
This educational content is part of a series of tutorials aimed at teaching the principles of physics through engaging and practical examples.
The transcript concludes with an encouragement for viewers to engage with the content creator through subscriptions, Patreon support, and email communication.
Transcripts
Browse More Related Video

Projectile Launched of a Cliff

Horizontally launched projectile | Two-dimensional motion | Physics | Khan Academy

Solving Projectile Motion Problems in Physics - [1-4-7]

Regents Physics: Angled Projectile Problem Practice
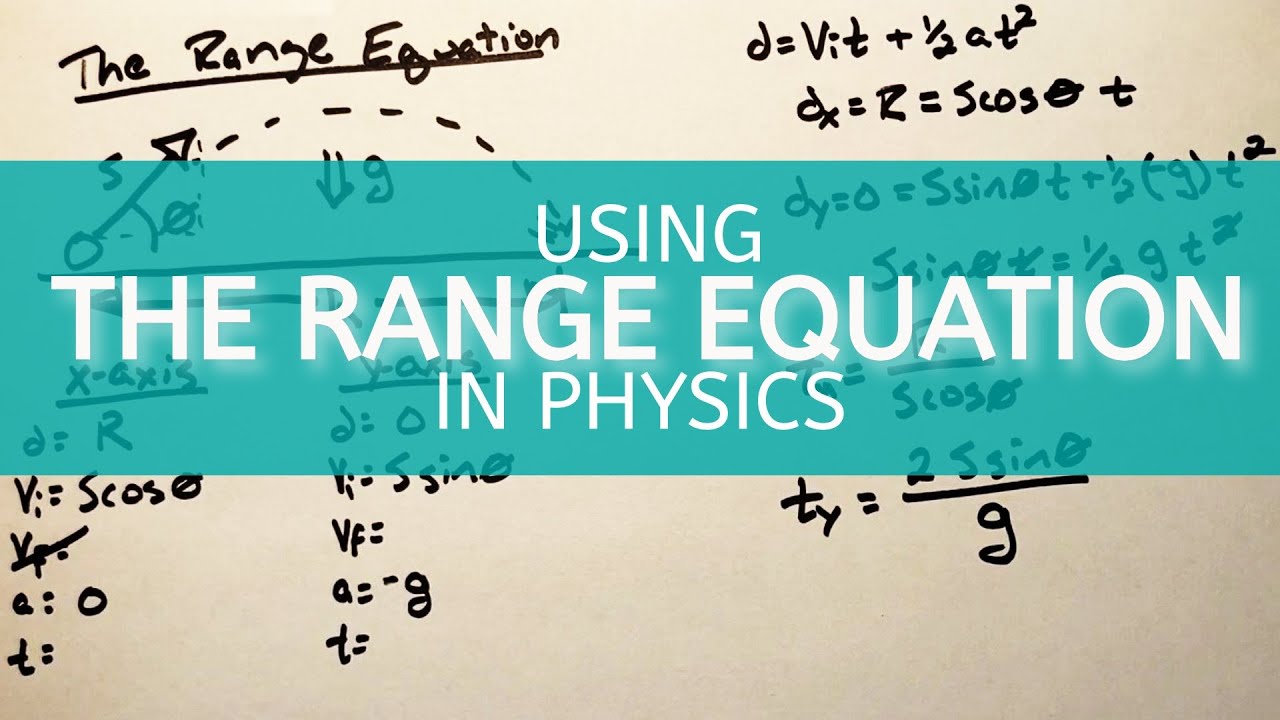
Where Does The Range Equation Come From?

College Physics 1: Lecture 12 - Projectile Motion
5.0 / 5 (0 votes)
Thanks for rating: