Rotational version of Newton's second law | Physics | Khan Academy
TLDRThe video script delves into the concept of torque and its significance in physics, deriving the rotational analog of Newton's second law. It explains how torque, the rotational force, relates to angular acceleration through the moment of inertia, which is analogous to mass in linear motion. The script simplifies the derivation by assuming a 90-degree force application and demonstrates how to calculate the net torque and moment of inertia for a system with multiple masses, concluding with a formula for angular acceleration that highlights the role of rotational inertia in resistance to angular motion.
Takeaways
- 🔧 Torque is a crucial concept in physics as it helps us understand how objects rotate and angularly accelerate.
- 📚 Newton's second law is foundational, relating force to acceleration, and there's a rotational analog that relates torque to angular acceleration.
- 🌀 The formula for torque is simplified when the force is applied at a right angle (90 degrees) to the radius, making the sine of the angle equal to one.
- 🔄 Angular acceleration is related to torque through a formula that includes the moment of inertia, which is analogous to mass in linear motion.
- 📉 Moment of inertia, often symbolized by I, is a measure of an object's resistance to changes in its rotation, similar to how mass is a measure of resistance to changes in linear motion.
- 🔢 The moment of inertia for a point mass rotating in a circle is calculated as I = MR^2, where M is the mass and R is the radius.
- ⚖️ The units of moment of inertia are kilogram meters squared (kg·m²), reflecting its composition of mass and the square of the radius.
- 🤔 In more complex systems with multiple masses, the total moment of inertia is found by summing the individual moments of inertia of each mass.
- 📐 When calculating torque in a system with multiple forces, it's essential to consider the correct radius for each force and the direction of the torque.
- 📉 The net torque in a system is calculated by considering the individual torques from each force, taking into account their direction and magnitude.
- 🛠️ The angular acceleration can be found using the derived formula, which is the net torque divided by the moment of inertia, and it indicates the rate at which an object will start to rotate or change its rotation speed.
Q & A
What is the purpose of deriving a rotational analog to Newton's second law?
-The purpose is to establish a formula that relates torque to angular acceleration, similar to how Newton's second law relates force to linear acceleration.
Why is torque necessary for angular acceleration?
-Torque is necessary because it is the force that causes an object to rotate or angularly accelerate. It is the rotational equivalent of linear force.
What is the formula for torque in the context of the video?
-In the context of the video, the formula for torque is simplified to F times R, where F is the force causing the torque and R is the distance from the axis to the point where the force is applied.
Why is it important to consider the sine of the angle (theta) when calculating torque?
-The sine of the angle is important because it determines the component of the force that is perpendicular to the radius, which is the effective part of the force contributing to the torque.
How does the video simplify the calculation of torque?
-The video simplifies the calculation by assuming the force is applied at a 90-degree angle to the radius (sine of 90 is 1), and considering the force as the net force acting on the object.
What is the relationship between torque and angular acceleration in the derived formula?
-The derived formula shows that torque is equal to the product of the mass, the square of the radius, and the angular acceleration (alpha).
What is the term 'moment of inertia' and why is it important in rotational dynamics?
-Moment of inertia (I) is a measure of an object's resistance to changes in its rotation. It is analogous to mass in linear dynamics and is important because it determines how difficult it is to angularly accelerate an object.
What are the units of moment of inertia and what does this indicate?
-The units of moment of inertia are kilogram meters squared (kg·m²). This indicates that it is a measure of mass distributed at a distance from the axis of rotation.
How is the moment of inertia calculated for a point mass in circular motion?
-For a point mass in circular motion, the moment of inertia is calculated as the mass (M) times the square of the radius (R) squared, or M * R².
What is the significance of considering the net torque and net force in a system with multiple forces?
-Considering the net torque and net force is important because it accounts for all the forces acting on the system. This ensures that the calculations for angular acceleration are accurate, taking into account both the magnitude and direction of the forces.
How can the moment of inertia be calculated for a system with multiple masses?
-For a system with multiple masses, the total moment of inertia is the sum of the individual moments of inertia for each mass, calculated as the mass of each point times the square of its distance from the axis of rotation.
Outlines
🔍 Deriving the Rotational Analog of Newton's Second Law
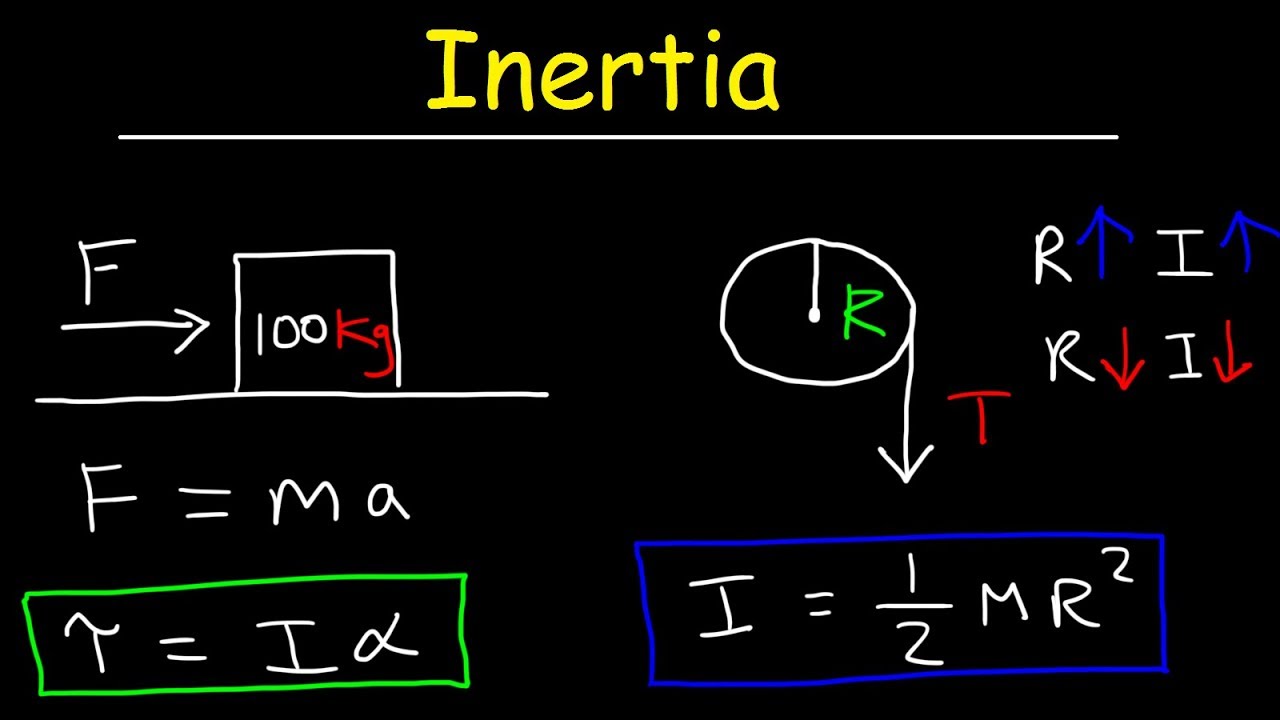
The instructor begins by emphasizing the importance of torque and its relation to angular acceleration. The goal is to establish a rotational equivalent to Newton's second law, which would allow predicting angular acceleration based on torque. The discussion revolves around the need for a tangential force to cause angular acceleration and the simplification of the torque formula by assuming a 90-degree angle, making sine theta equal to one. The instructor then multiplies both sides of the force equation by the radius to incorporate torque, leading to the realization that torque is directly proportional to the product of mass, radius, and angular acceleration. The summary concludes with the derivation of the formula that equates torque to mass times radius squared times angular acceleration, introducing the concept of moment of inertia as the rotational analog to mass.
📚 Understanding Moment of Inertia and Its Role in Angular Acceleration
This paragraph delves deeper into the concept of moment of inertia, explaining its significance as a measure of an object's resistance to angular acceleration, similar to how mass is a measure of resistance to linear acceleration. The instructor clarifies that moment of inertia, represented by 'I', is the sum of mass times the square of the radius (MR^2). It is highlighted that a larger moment of inertia indicates a greater difficulty in achieving angular acceleration. The concept is exemplified using a ball on a string, where the moment of inertia is calculated as MR^2. The instructor also touches upon the historical term 'moment of inertia' versus the more descriptive 'rotational inertia' and notes the units of moment of inertia as kilogram meters squared. The paragraph concludes with a cautionary note about considering net forces and torques when dealing with multiple forces acting on an object.
🔧 Calculating Angular Acceleration with Multiple Forces and Masses
The final paragraph presents a complex scenario involving multiple forces and masses to illustrate the application of the derived rotational Newton's second law. The instructor demonstrates how to calculate the net torque by considering individual torques from different forces, taking into account their respective distances from the axis of rotation (R) and their directions. The importance of correctly assigning signs to torques based on their rotational effect (positive for counterclockwise, negative for clockwise) is emphasized. The calculation of moment of inertia for a system of masses is explained as the sum of individual moments of inertia (MR^2 for each mass). An example calculation is provided, where the individual contributions of three different masses to the total moment of inertia are added together, and the resulting angular acceleration is computed to be 1.83 radians per second squared. The summary underscores the parallel between Newton's second law for linear motion and its rotational counterpart, which relates torque to angular acceleration through the lens of rotational inertia.
Mindmap
Keywords
💡Torque
💡Newton's Second Law
💡Angular Acceleration
💡Moment of Inertia
💡Tangential Force
💡Radius
💡Net Force
💡Rotational Analog
💡Sine Theta
💡Point Mass
💡Net Torque
Highlights
Derivation of the rotational analog of Newton's second law for objects rotating in a circle.
Introduction of the concept of torque and its role in causing angular acceleration.
Explanation of the need for a force tangential to the circle for angular acceleration.
Simplification of the torque formula by setting the angle to 90 degrees to make sine theta equal to one.
Relating torque to the net force and mass of an object to derive the rotational formula.
Multiplication of both sides of the force equation by the radius to incorporate torque.
Identification of the need to replace regular acceleration with angular acceleration in the formula.
Introduction of the relationship between tangential acceleration and angular acceleration.
Rewriting the tangential acceleration as a function of angular acceleration (R times alpha).
Derivation of the formula for torque as M times R squared times alpha.
Introduction of the moment of inertia (I) as the rotational analog to mass in Newton's second law.
Explanation of how moment of inertia (I) represents the rotational inertia of a system.
Description of the units of moment of inertia as kilogram meters squared.
Discussion on the impact of mass and radius on the difficulty of angularly accelerating an object.
Consideration of multiple forces and torques in the system and how to calculate net torque.
Explanation of how to calculate the moment of inertia for a system of masses by summing individual contributions.
Application of the derived formula to a complex problem involving multiple masses and forces.
Calculation of the angular acceleration for a system with given forces and masses.
Recap of the rotational Newton's second law and its relation to angular acceleration and rotational inertia.
Transcripts
Browse More Related Video

College Physics 1: Lecture 25 - Moment of Inertia and Rotational Dynamics

AP Physics 1 - Rotational Dynamics

Torque: Crash Course Physics #12

Physics 15 Torque Fundamentals (13 of 13) Torque and Angular Acceleration
Inertia - Basic Introduction, Torque, Angular Acceleration, Newton's Second Law, Rotational Motion

Demonstrating Rotational Inertia (or Moment of Inertia)
5.0 / 5 (0 votes)
Thanks for rating: