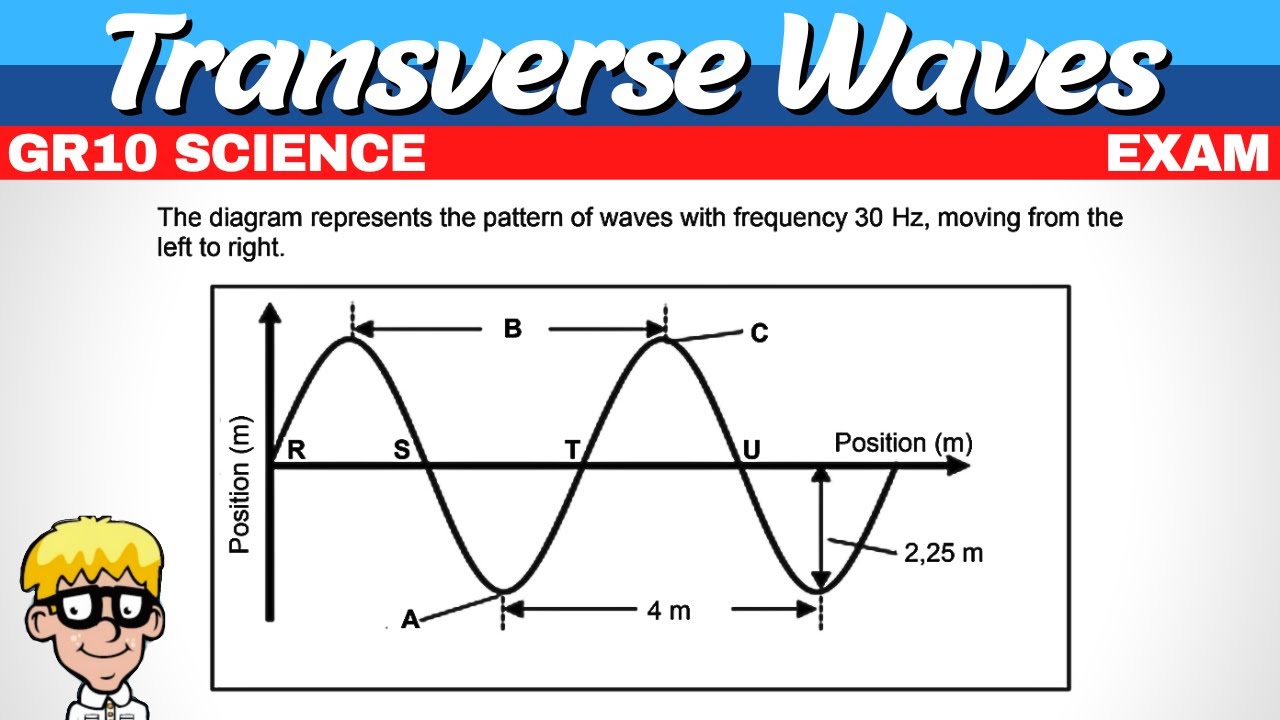
Waves - Frequency, Speed, and Wavelength (NEWER vid)
TLDRThe video script delves into the fundamental concepts of wave properties, focusing on frequency, speed, and wavelength. It explains that frequency, measured in hertz, is the rate of occurrence of wave cycles per second and is determined by the source of the wave, not the speed. The script clarifies that wave speed is constant for waves in the same medium and is independent of frequency. It further illustrates the relationship between frequency and wavelength, where higher frequencies correspond to shorter wavelengths and vice versa, assuming a constant wave speed. The video employs simulations and analogies, such as comparing waves to cars crossing a toll plaza, to effectively demonstrate these principles and their practical implications.
Takeaways
- 📈 Frequency is the rate at which something occurs, measured in cycles per second or Hertz (Hz).
- 🌊 A wave cycle is a complete set of oscillations from one point on a wave to the same point on another wave, typically measured from crest to crest or trough to trough.
- 🔊 The source of a wave determines its frequency, not the speed at which the wave travels through a medium.
- 🚀 Regardless of frequency, waves of the same type traveling through the same medium have the same speed.
- 🌀 Higher frequency waves have shorter wavelengths, while lower frequency waves have longer wavelengths, assuming the wave speed is constant.
- 📌 The relationship between frequency, wave speed, and wavelength can be expressed by the formula: frequency (Hz) = wave speed (m/s) / wavelength (m).
- 🔄 The frequency of a wave is intrinsically linked to the oscillation rate of its source, not the velocity of the wave itself.
- 🛤️ When a wave crosses into a new medium, its speed may change, but its frequency remains constant, causing the wavelength to adjust accordingly.
- 🚦 The analogy of cars crossing a toll plaza illustrates how shorter wavelengths (like shorter cars) can pass by at a higher frequency than longer wavelengths (like longer cars).
- 📝 Practice problems help solidify the understanding of the relationship between frequency, wavelength, and wave speed.
- 📚 The concepts discussed are fundamental to the study of wave properties and behavior in various mediums.
Q & A
What is frequency in the context of waves?
-In the context of waves, frequency refers to the number of cycles or wavelengths that occur every second. It is measured in hertz (Hz), where one hertz equals one cycle per second.
How is a cycle defined in wave terminology?
-A cycle in wave terminology is defined as one full wavelength, which can be measured from a point on one wave to the same point on another wave. It can be measured from crest to crest, trough to trough, or any other corresponding points on each wave.
What are the units used to measure frequency and how is it abbreviated?
-The unit used to measure frequency is Hertz (Hz), which is abbreviated as 'Hz'. One Hz represents one cycle per second.
What is the relationship between the number of waves and the frequency of a wave?
-The frequency of a wave is directly proportional to the number of waves. The more waves that pass a certain point in one second, the higher the frequency. Conversely, fewer waves per second result in a lower frequency.
How does the source of a wave affect its frequency?
-The source of a wave determines its frequency. The faster the source oscillates, the higher the frequency of the waves it generates. If the source moves slower, the frequency is lower.
What is wave speed and how is it related to frequency and wavelength?
-Wave speed is the rate at which individual wave crests or points on a wave move through a medium. It is determined by the medium through which the wave is traveling. Wave speed does not change with frequency; instead, it is the wavelength that changes if the speed changes. For waves of the same frequency traveling through the same medium, the speed remains constant.
What happens to the wavelength when the wave speed changes?
-When the wave speed changes, the wavelength adjusts proportionally. If the wave speed increases, the wavelength becomes longer; if the wave speed decreases, the wavelength becomes shorter. This ensures that the frequency, determined by the source, remains constant when the wave travels through different media.
How can you calculate the wavelength of a wave given its frequency and speed?
-The wavelength of a wave can be calculated using the formula: wavelength = wave speed / frequency. By dividing the speed of the wave (in meters per second) by its frequency (in hertz), you obtain the wavelength in meters.
What is the analogy used in the script to explain the relationship between frequency and wavelength?
-The script uses an analogy involving cars of different lengths (short and long) crossing a bridge (toll plaza) at a constant speed. The short cars (higher frequency waves) can pass through more frequently because they take less time to cross, similar to how higher frequency waves have shorter wavelengths. Conversely, the long cars (lower frequency waves) pass less frequently due to their longer length, analogous to lower frequency waves having longer wavelengths.
How does the medium through which a wave travels affect its speed and wavelength?
-The medium through which a wave travels determines its speed. When a wave enters a new medium, its speed may change, which in turn affects its wavelength. If the wave speed increases, the wavelength lengthens; if the wave speed decreases, the wavelength shortens. However, the frequency, determined by the source, remains unchanged when the wave crosses into a new medium.
What is the correct way to express the relationship between wave frequency, wave speed, and wavelength?
-The correct relationship is expressed by the formula: wavelength = wave speed / frequency. This formula indicates that the wavelength is the result of the wave's speed (determined by the medium) divided by the frequency (determined by the source).
Outlines
📊 Introduction to Wave Concepts: Frequency, Wavelength, and Speed
This paragraph introduces fundamental concepts related to waves, focusing on frequency, wavelength, and speed. Frequency is defined as the rate at which events occur, and in the context of waves, it is measured in cycles per second or hertz (Hz). The explanation includes examples of how to calculate frequency based on the number of waves passing a point in a given time. The paragraph also clarifies that the source of the wave determines its frequency, and that higher frequency does not necessarily mean faster wave speed. The relationship between frequency and wavelength is established, with the medium through which the wave travels being the key factor in determining wave speed. The concept is further illustrated through a simulation where adjusting the frequency affects the source's oscillation rate but not the wave's speed through the same medium.
🌉 The Relationship Between Wave Speed, Frequency, and Wavelength
This paragraph delves deeper into the relationship between wave speed, frequency, and wavelength. It demonstrates that while wave speed can vary depending on the medium, frequency remains constant as it is determined by the source of the wave. A simulation is used to show that even when wave speed changes due to a different medium, the frequency stays the same. The analogy of cars crossing a bridge is used to explain that higher frequency waves, like shorter cars, can pass by more frequently than lower frequency waves, which are likened to longer cars. The mathematical relationship between wave speed, frequency, and wavelength is also introduced, with the formula frequency equals velocity over wavelength. The paragraph emphasizes that wavelength is the result of the wave's velocity divided by its frequency, and concludes with practice problems to reinforce the concepts learned.
Mindmap
Keywords
💡Frequency
💡Wave
💡Speed
💡Wavelength
💡Cycle
💡Amplitude
💡Hertz
💡Simulation
💡Medium
💡Practice Problems
💡Analogies
Highlights
Frequency is defined as the rate at which something occurs, such as the number of quizzes per week.
In the context of waves, frequency refers to the number of cycles per second or waves per second.
A cycle is equivalent to one full wavelength and can be measured from corresponding points on successive waves.
The unit for cycles per second is Hertz (Hz), with one Hz equaling one cycle per second.
The frequency of a wave is determined by the source of the wave, not the medium it travels through.
Wave speed is determined by the medium and remains constant regardless of frequency changes.
If two waves travel through the same medium, they have the same speed despite potentially different frequencies.
A change in wave speed results from a change in the medium, not from changes in frequency.
The relationship between frequency and wavelength is inversely proportional; higher frequency corresponds to shorter wavelength and vice versa.
The formula for frequency is the velocity of the wave divided by its wavelength.
The wavelength is the result of the wave's velocity divided by its frequency from the source.
A wave source provides energy at a specific frequency, which travels through a medium at a certain speed to produce a wave with a particular wavelength.
The analogy of cars crossing a toll plaza illustrates how frequency relates to wavelength, with shorter cars (waves) passing through more frequently than longer ones.
The ratio of wave speed to wavelength is constant for a given frequency.
Understanding the relationship between frequency, wavelength, and wave speed is essential for various practical applications and theoretical studies.
The content provided is a comprehensive guide to the concepts of wave frequency, wavelength, and speed, suitable for educational purposes.
Practice problems are offered to reinforce the understanding of the discussed concepts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: