Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (12 of 92) Time & Position Dependencies 1/3

Michel van Biezen
8 Feb 201704:19
EducationalLearning
32 Likes 10 Comments

TLDRIn this video, the presenter delves into the process of separating the time and position dependencies of the Schrödinger equation. By illustrating the advantage of expressing famous physical systems like the wave equation for the hydrogen atom as standing waves, the video demonstrates how to rewrite the one-dimensional wave equation as a product of two wave functions, one for position and one for time. This separation simplifies the equation, making it easier to solve. The video then shows how to substitute this separated form back into the original equation, leading to two new, simpler differential equations that can be solved individually. The goal is to derive separate equations for position and time functions, which is crucial for quantum mechanics applications with small particles.

Takeaways
  • 🌟 The goal is to separate the time and position dependencies of the Schrödinger equation to simplify its analysis.
  • 📈 Famous examples like the wave equations for the bore atom and the simple harmonic oscillator can be expressed in terms of standing waves, which are time-independent.
  • 🌊 The wave equation in one dimension is initially dependent on both position and time, and the aim is to express it as a product of two wave functions, one for position and one for time.
  • 🔄 By substituting the separated wave functions back into the original Schrödinger equation, we can simplify the mathematical operations involving partial derivatives.
  • 📝 After separation, dividing both sides of the equation by the product of the position and time-dependent wave functions yields two new equations with distinct dependencies.
  • 🔢 The division process results in each side of the equation being dependent on only one variable, position or time, respectively.
  • 🎓 Each side of the equation must be equal to the same constant, denoted as C, which allows for the formulation of two separate differential equations.
  • 🌈 The new form of the Schrödinger equation is easier to solve due to the transformation into normal differentiation and the separation of variables.
  • 🔍 The next steps involve solving these differential equations to derive new waveforms for quantum mechanics applications.
  • 💡 The process demonstrates the advantage of separating variables to simplify complex wave equations and make them more manageable for further analysis.
  • 📚 The video series will continue to guide through the solution of these equations and their application in understanding quantum mechanics.
Q & A

  • What is the main goal of separating the time and position dependencies in the Schrödinger equation?

    -The main goal is to simplify the equation by reducing it to a form that is easier to work with, allowing for a more straightforward solution process, similar to how standing waves can be used to express the wave equations for the boron atom and the simple harmonic oscillator.

  • What is the initial form of the wave function in the one-dimensional Schrödinger equation?

    -Initially, the wave function is a single function that depends on both position and time.

  • How does the separation process change the original wave function?

    -The separation process rewrites the original wave function as a product of two functions, one dependent on position and the other on time.

  • What happens when the separated wave functions are substituted back into the original Schrödinger equation?

    -Upon substitution, the original equation is transformed into two separate equations, each involving only one of the separated variables (position or time).

  • Why is dividing both sides of the equation by the product of the separated wave functions useful?

    -This division isolates the dependencies on position and time on each side of the equation, allowing for the simplification of the equation into a more manageable form.

  • What is the significance of the constant C in the separated equations?

    -The constant C indicates that each side of the separated equation must be equal to the same constant, which simplifies the process of solving the differential equations.

  • How does the separation process affect the differentiation within the equations?

    -After separation, the partial derivatives with respect to x and t become normal derivatives since each function now depends on only a single variable.

  • What are the new forms of the Schrödinger equation obtained after separation?

    -The new forms are two separate differential equations, one involving only the position-dependent function and the other only the time-dependent function.

  • How will the separated equations be used in future videos?

    -In upcoming videos, the separated equations will be solved, and the solutions will be used to derive two new waveforms for working with small particles in quantum mechanics.

  • What is the advantage of expressing the wave equations for the boron atom and the simple harmonic oscillator in terms of standing waves?

    -Expressing these wave equations in terms of standing waves allows them to be time-independent, simplifying their analysis and understanding.

  • What is the role of the potential energy term in the separated Schrödinger equation?

    -The potential energy term remains in the separated equation that is dependent on position, indicating that it still influences the spatial behavior of the wave function.

Outlines
00:00
🌟 Separating Time and Position in the Schrödinger Equation

The paragraph introduces the concept of separating the time and position dependencies in the Schrödinger equation. It explains the advantage of this separation by referencing famous examples like the wave equations for the hydrogen atom and the simple harmonic oscillator, which can be expressed as standing waves and thus are independent of time. The goal is to rewrite the wave equation in one dimension as a product of two wave functions, one dependent on position and the other on time. This simplification makes the equation easier to work with and leads to a more manageable form of the Schrödinger equation, which will be solved in the upcoming videos. The process involves substituting the separated wave functions back into the original equation and dividing both sides by the product of the position and time-dependent wave functions, resulting in two separate equations, each depending only on a single variable (position or time). This method is crucial for solving quantum mechanics problems involving small particles.

Mindmap
Keywords
💡Electrodynamics
Electrodynamics is a branch of physics that deals with the study of the dynamics of charged particles and the electromagnetic fields they generate. In the context of the video, electrodynamics is the underlying field of study for the Schrödinger equation, which describes how quantum systems evolve over time. The video aims to simplify the complex equations in electrodynamics by separating time and position dependencies, making it easier to understand and solve.
💡Schrödinger Equation
The Schrödinger Equation is a fundamental equation in quantum mechanics that describes how the quantum state of a physical system changes with time. It is a partial differential equation that combines both position and time dependencies. The video focuses on separating these dependencies to simplify the equation and make it more manageable for solving quantum mechanical problems.
💡Wave Equation
A wave equation is a mathematical model that describes the propagation of waves in a medium or space. In the context of the video, the wave equation is used as an analogy to the Schrödinger Equation, highlighting that famous physical systems like the bore atom and the simple harmonic oscillator can be described in terms of standing waves, which are solutions to the wave equation that do not depend on time.
💡Standing Waves
Standing waves are patterns of wave vibration that appear to stand still in space. They are created by the superposition of two waves of the same frequency and amplitude traveling in opposite directions. In the video, standing waves are mentioned as a desirable state because they do not depend on time, simplifying the mathematical treatment of physical systems.
💡Position and Time Dependencies
In the context of the video, position and time dependencies refer to the variables that the Schrödinger Equation depends on to describe the quantum state of a system. The goal is to separate these dependencies to simplify the equation, making it easier to solve. By writing the equation as a product of two functions, one dependent on position and the other on time, the complexities of the original equation are reduced.
💡Wave Functions
Wave functions are mathematical functions used in quantum mechanics to describe the quantum state of a system. They contain all the information about the system's physical properties. In the video, the wave function is separated into two components, one that depends on position and another on time, allowing for the simplification of the Schrödinger Equation.
💡Partial Derivative
A partial derivative is a mathematical operation that deals with functions of multiple variables by finding the derivative with respect to one variable while treating the other variables as constants. In the video, the process of separating the Schrödinger Equation involves taking partial derivatives with respect to both position and time, which leads to the separation of the time and position dependencies.
💡Constant
In mathematics, a constant is a value that does not change. In the context of the video, after separating the Schrödinger Equation, each side of the resulting equation is found to be equal to a constant value, denoted as C. This constant represents the separation constant, which is a key step in simplifying the equation and solving for the wave functions.
💡Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at the atomic and subatomic scales. It is the foundation for understanding the behavior of particles in the microscopic world. The video discusses the Schrödinger Equation, which is a cornerstone of quantum mechanics, and how to simplify it for solving problems involving small particles.
💡Solving Differential Equations
Solving differential equations involves finding the functions that satisfy a given equation. In the context of the video, the goal is to solve the separated forms of the Schrödinger Equation, which are simpler differential equations compared to the original. The process involves separating the time and position dependencies to make the equations easier to solve.
💡Small Particles
In the context of the video, small particles refer to microscopic entities such as electrons, protons, and neutrons that are the subject of quantum mechanics. The simplification of the Schrödinger Equation is particularly relevant for understanding the behavior of these small particles in quantum systems.
Highlights

The goal is to separate the time and position dependencies of the Schrödinger equation.

Famous examples like the wave equations for the bore atom and the simple harmonic oscillator can be expressed in terms of standing waves, which do not depend on time.

Separating dependencies makes the equation easier to work with.

The process starts with the one-dimensional wave equation.

The wave function is written as a product of two functions, one dependent on position and one on time.

Substituting the separated wave function back into the Schrödinger equation is the next step.

The partial second derivative with respect to x is now a product of two functions, simplifying the equation.

Dividing both sides of the equation by the product of the wave functions separates the position and time dependencies.

Each side of the equation must be equal to the same constant, which is denoted as C.

The partial differentiation turns into normal differentiation as it's only dependent on a single variable.

The resulting two equations are a new form of the Schrödinger equation, easier to solve.

The next videos will show how to solve this differential equation and find the wave functions.

The aim is to come up with separate equations, one using only a function of position and one using only a function of time.

This method is particularly useful when dealing with small particles in quantum mechanics.

The process simplifies the complex Schrödinger equation into more manageable parts.

Standing waves are key to expressing certain equations without time dependence.

The method allows for the derivation of two new waveforms for quantum mechanics applications.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (14 of 92) Time & Position Dependencies 3/3

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (5 of 92) The Schrodinger Eqn. in 1-D (1/3)

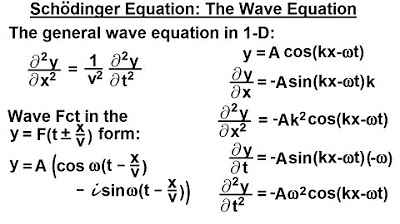
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (3 of 92) The Wave Equation

24. Quantum Mechanics VI: Time-dependent Schrödinger Equation

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (13 of 92) Time & Position Dependencies 2/3

The equation of a wave | Physics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsSchrödingerEquationWaveFunctionsPhysicsTutorialMathematicsEducationalContentOnlineLearningScienceExplorationTimeIndependencePositionFunctions