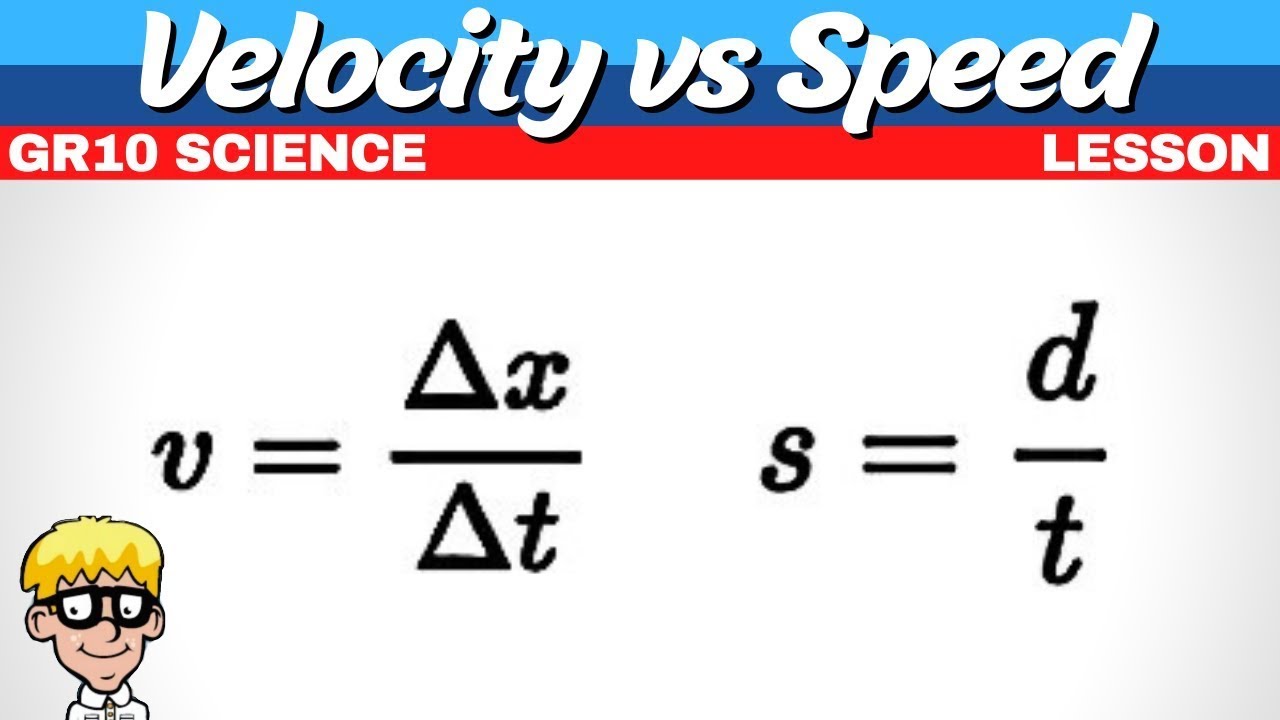Kinematics Physics Formulas
TLDRThis video delves into the fundamentals of kinematics, focusing on key concepts such as displacement, velocity, and acceleration. It explains displacement as a vector quantity and velocity as the rate of change of displacement over time. The distinction between speed and velocity is clarified, with speed being a scalar and velocity a vector. Acceleration is introduced as the rate of change of velocity. The video also explores the differences between average and instantaneous velocity and acceleration. Furthermore, it provides a comprehensive guide to various kinematic formulas, including those for constant velocity and acceleration, and explains how to derive the formula for final velocity in terms of initial velocity, acceleration, and displacement. The video concludes with resources for further practice and study.
Takeaways
- 📌 Kinematics studies motion, including both one-dimensional motion (along the x-axis) and two-dimensional motion (along the x and y axes).
- 🔄 Displacement (Δx, Δy) is a vector quantity representing the change in position (final minus initial), while distance is a scalar quantity without direction.
- 🚀 Velocity is the rate of change of displacement with respect to time (D/t), and it is a vector quantity with both magnitude and direction, unlike speed, which is a scalar and only has magnitude.
- 🔽 Acceleration is the rate of change of velocity over time (ΔV/ΔT), calculated by finding the difference between final and initial velocities and dividing by the time interval.
- 🔄 The difference between average velocity (displacement/time) and instantaneous velocity is that the latter is found using the limit function as the time interval approaches zero.
- 🔄 Similarly, average acceleration is the change in velocity over time, while instantaneous acceleration is found by making the time interval very small in the formula ΔV/ΔT.
- 📈 The formula for displacement when constant acceleration is involved is D = (V_initial * t) + (1/2) * a * t^2, which is derived from the basic kinematic equations.
- 📊 The kinematic formula v^2 = u^2 + 2as can be derived by combining and rearranging other basic kinematic equations, showing the relationship between final velocity, initial velocity, and displacement.
- 🔗 Access to additional kinematics practice problems and videos is available on the tutor's Patreon page, offering extended content and worksheets.
- 🎓 The video also covers other physics topics such as vectors, projectile motion, and various concepts related to forces and energy, with extended videos and practice problems available.
Q & A
What is the primary focus of the video?
-The primary focus of the video is to discuss kinematics, specifically the formulas used in the study of motion in physics.
What are the two types of motion described in the video?
-The two types of motion described are Motion in One Direction (along the x-axis) and Motion in Two Dimensions (along both the x and y axes).
How is displacement different from distance?
-Displacement is a vector quantity that represents the change in position with direction, while distance is a scalar quantity that represents the total path length traveled without direction.
What is the formula for calculating velocity?
-The formula for calculating velocity is the change in displacement (Δx or Δy) over the change in time (Δt), which can be represented as Δx/Δt or Δy/Δt.
What is the difference between speed and velocity?
-Speed is the absolute value of velocity and is a scalar quantity with only magnitude, while velocity is a vector quantity with both magnitude and direction.
How is acceleration defined in kinematics?
-Acceleration is defined as the rate of change of velocity over time, which can be calculated as the change in velocity (ΔV) over the change in time (Δt), represented as ΔV/Δt.
What is the significance of the limit function in calculating instantaneous velocity?
-The limit function is used to calculate instantaneous velocity by making the time interval (Δt) approach zero, providing a more accurate estimate of the velocity at a specific point in time.
What is the formula for displacement when constant acceleration is involved?
-The formula for displacement with constant acceleration is D = V_initial * t + 0.5 * a * t^2.
How can you derive the formula for V_final squared equals V_initial squared plus two times a times d?
-This formula can be derived by combining the equations for displacement (D = V_initial * t + 0.5 * a * t^2) and the relationship between final and initial velocity (V_final = V_initial + a * t), and rearranging them to isolate V_final squared.
Where can one find additional practice problems on kinematics?
-Additional practice problems on kinematics can be found on the Patreon page of the math science tutor, as well as in the description section of the video on YouTube.
What is the difference between average velocity and instantaneous velocity?
-Average velocity is the total displacement divided by the total time taken, while instantaneous velocity is the velocity at a specific moment in time, calculated using the limit as the time interval approaches zero.
Outlines
📐 Introduction to Kinematics and Basic Concepts
This paragraph introduces the topic of kinematics, focusing on motion in one or two dimensions and the key concept of displacement. Displacement is defined as the change in position (final position minus initial position) along the x-axis (Δx) and y-axis (Δy). The distinction between distance and displacement is clarified, with displacement being a vector quantity (having both magnitude and direction) and distance being a scalar quantity (having only magnitude). The paragraph also explains the concept of velocity as the rate of change of displacement with respect to time (D/t), highlighting the difference between speed (a scalar) and velocity (a vector). Acceleration is introduced as the rate of change of velocity over time (ΔV/ΔT), with examples provided for calculating both velocity and acceleration.
🎯 Accessing Practice Problems and Additional Resources
The speaker guides the audience on how to access more practice problems and resources related to kinematics. The main platform mentioned is the speaker's Patreon page, where subscribers can access extended videos, practice problems, and worksheets. The speaker also mentions a specific video on 'Free Fall problems' and other physics topics such as vectors, projectile motion, and static friction. The Patreon page is highlighted as the place to find extended versions of the videos and additional practice problems, with a six-hour long physics final exam review video available. The speaker also mentions a YouTube membership program and provides information on how to access the content through direct links in the video description.
📈 Understanding Average vs. Instantaneous Velocity and Acceleration
This paragraph delves into the differences between average and instantaneous velocity, as well as average and instantaneous acceleration. The speaker explains how to calculate average velocity over a time interval and how to use the limit function to approximate instantaneous velocity as the time interval becomes smaller. The concept of instantaneous acceleration is also discussed, with the formula ΔV/ΔT and its application to estimate the acceleration at a specific time by making ΔT very small. The paragraph emphasizes the use of limits to achieve accurate estimates of instantaneous values in kinematics.
🧠 Derivation and Application of Kinematic Formulas
The speaker discusses various kinematic formulas, including the relationship between displacement, constant velocity, and time, as well as the formula for constant acceleration (D = (V_initial + V_final)/2 * t + 0.5 * a * t^2). The derivation of the formula V_final^2 = V_initial^2 + 2 * a * d is explored in detail, showing how it can be derived from two other kinematic formulas. The explanation includes rearranging equations to solve for time and then substituting values back into the displacement formula. The paragraph concludes with an encouragement for viewers to practice using these formulas and to access additional resources and practice problems through provided links.
Mindmap
Keywords
💡Kinematics
💡Displacement
💡Velocity
💡Acceleration
💡Practice Problems
💡Average Velocity
💡Instantaneous Velocity
💡Average Acceleration
💡Constant Velocity
💡Constant Acceleration
💡Kinematic Formulas
Highlights
Introduction to kinematics and its relevance in physics.
Explanation of motion in one dimension and two dimensions along the x-axis and both x and y axes.
Definition of displacement as a vector quantity with the formula Delta X for horizontal displacement and Delta Y for vertical displacement.
Description of velocity as the rate of change of displacement with respect to time, given by D over t.
Differentiation between speed and velocity, emphasizing that speed is a scalar quantity without direction, while velocity is a vector with both magnitude and direction.
Formula for calculating velocity in the x-direction as the change in x over the change in time.
Explanation of acceleration as the rate of change in velocity over time, using the formula Delta V over delta T.
Access to more practice problems on kinematics through the provided Patreon link.
Details on the structure of the Patreon page and how to navigate to the physics section for extended videos and worksheets.
Mention of specific kinematics topics covered in the Patreon videos, such as free fall problems, vectors, projectile motion, and relative velocity.
Information on the availability of extended videos on various physics topics and the physics final exam review video.
Explanation of the difference between average velocity and instantaneous velocity, and how to approximate instantaneous velocity using limits.
Formula for average acceleration and how to calculate instantaneous acceleration by making delta T very small.
Derivation of the kinematic formula displacement equals initial velocity times time plus one half times acceleration times time squared.
Introduction to the kinematic formula for constant acceleration, where average velocity is the sum of initial and final velocity divided by 2.
Derivation of the final kinematic formula, V final squared equals V initial squared plus two times acceleration times displacement (Vf^2 = Vi^2 + 2ad).
Conclusion of the video with a summary of the key kinematic formulas and an invitation to practice using the provided resources.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: